Espera-se que, ao final desta aula, o aluno seja capaz de fazer rotações de figuras geométricas planas apresentadas no sistema cartesiano, dados um ponto (centro) e um ângulo.

1 ou 2 aulas 50 minutos cada

- Conceito de vetor

- Representação de pontos e vetores no plano cartesiano

- Trigonometria

Sugerimos que, a partir da ideia de rotação, os arcos e suas medidas surjam naturalmente. Portanto, apresentamos uma situação em que o ponteiro dos minutos de um relógio analógico gira continuamente e, a cada horário determinado por ele, um arco é identificado. Observe:

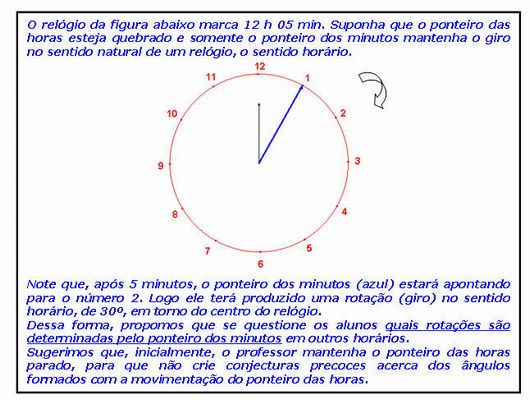
O objetivo central desta aula é apresentar, conceituar e visualizar a transformação de rotação de objetos matemáticos no plano (ponto, reta, vetor, segmento, figuras geométricas) em torno de um ponto dado e segundo um ângulo previamente estabelecido.

Sugerimos que, a partir a ideia de rotação surja naturalmente. Portanto, apresentamos uma situações em que os ponteiros de um relógio analógico giram continuamente. Observe:

A partir dessa ideia, sugerimos a introdução da noção de rotação:

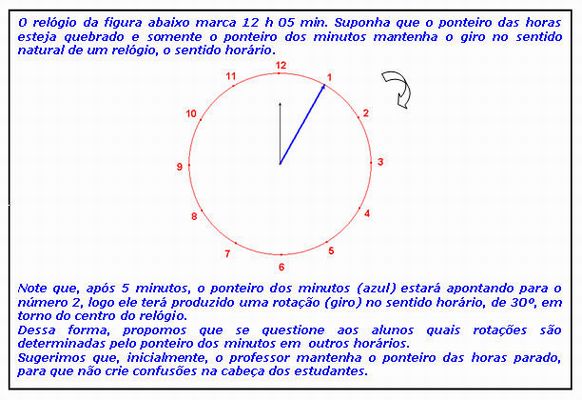
“A rotação é uma transformação que produz um giro de um objeto em torno de um centro fixo, segundo um ângulo determinado.”

Pode-se rotacionar um ponto, um vetor, um segmento, uma reta ou até uma figura, desde que sejam fixados o centro e o ângulo de rotaçã o.

Para que a tr ansformação de rotação de um vetor em torno de um ponto se ja visualizada, sugeri mos a apresentação da rotação no plano cartesiano, em torno da origem O, conforme as figuras abaixo:

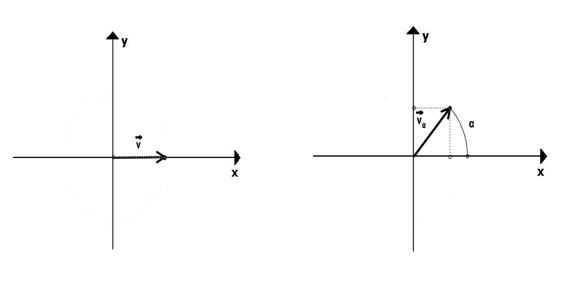
Posteriormente, apresentamos um exemplo no qual solicitamos as novas coordenadas do vetor (2, 0) quando rotacionado, no sentido anti-horário, em torno da origem sob um ângulo de medida 60°.

A partir da localização do vetor (2, 0) no plano cartesiano e a visualização da rotação, formam-se triângulos retângulos que abrem possibilidades de cálculos através das razões trigonométricas. Observe a figura: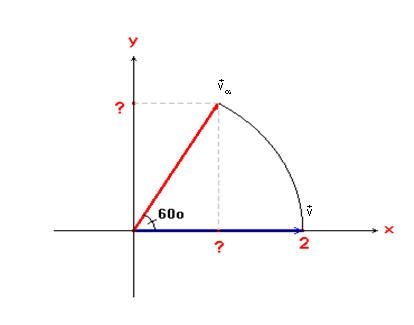

Consideramos relevante a apresentação de mais exemplos e o desenvolvimento de algumas atividades para que a aula atinja seu objetivo.

Para obter o detalhamento desta aula, com os conceitos apresentados, exemplos e atividades, clique no link abaixo.

http://www.cap.ufrj.br/matematica/PortaldoProfessorMec/atividades/Aula_Rotacao.pdf

http://www.cap.ufrj.br/matematica/PortaldoProfessorMec/atividades/Aula_Rotacao.pdf

http://www.cap.ufrj.br/matematica/PortaldoProfessorMec/atividades/Atividades_rotacao.pdf

Aplicação de atividades que abordem o tema para a fixação dos conteúdos apresentados.

O link abaixo apresenta sugestões de exercícios para serem aplicados ao final desta aula.

http://www.cap.ufrj.br/matematica/PortaldoProfessorMec/atividades/Atividades_rotacao.pdf