20/12/2009
Marco G. B. Burlamaqui
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Fundamental Final | Matemática | Espaço e forma |
| Ensino Fundamental Final | Matemática | Cálculo |
| Ensino Médio | Matemática | Tecnologia para a matemática |
| Ensino Fundamental Final | Matemática | Operações |
| Ensino Fundamental Final | Matemática | Grandezas e medidas |
| Ensino Fundamental Final | Matemática | Aritmética |
| Ensino Médio | Matemática | Álgebra |
| Ensino Médio | Matemática | Números e operações |
| Ensino Médio | Matemática | Geometria |
O que o aluno poderá aprender com esta aula
- Calcular a área total de um cilindro
- Calcular o volume de um volume
- Introdução ao uso do software de geometria dinâmica “Calques 3D” (livre) no processo de estudo das transformações geométricas, estimulando-se o treinamento e a familiaridade em aulas no laboratório informática.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
- Cálculo de área de figuras planas
- Cálculo do volume
Estratégias e recursos da aula
Olá Professor, apresente aos seus alunos o vídeo da aula 63 do antigo TeleCurso, caso não tenha na escola o mesmo esta disponível nos sítios:
· http://www.youtube.com/watch?v=fFNJQzPYYKI
· http://novotelecurso.blogspot.com/2009/07/cubo-prismas-cilindro.html
Apresente uma situação-problema para que os alunos possam refletir sobre o assunto, por exemplo:
Um empresário recebeu um pedido para fabricar determinando tipo de peça. Para cobrar pelo serviço, o dono da indústria precisa calcular a quantidade de matéria-prima necessária para a fabricação de cada unidade. Calcule a área total da superfície da peça, conforme as dimensões dadas a seguir:
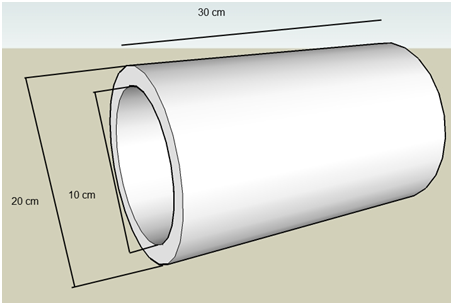
Imagem produzida no Google Sketchup
Professor a parte teórica sobre o assunto esta disponível em:
· http://www.vestibular1.com.br/revisao/cilindro.pps
· http://www.colegioweb.com.br/matematica/conceito-de-cilindro
· http://www.colegioweb.com.br/matematica/areas-e-volumes
· http://www.colegioweb.com.br/matematica/secao-meridiana-e-cilindro-equilatero
· http://www.somatematica.com.br/emedio/espacial/espacial14.php
· http://www.estudeonline.net/revisao_detalhe.aspx?cod=454
Uma boa atividade para trabalhar com os alunos é a construção do cone partindo de uma planificação. Nos sítios temos uma excelente atividade. Temos também planificações nos sítios:
· http://www.junior.te.pt/escolinha/anosLista.jsp?id=354&p=6&d=mat&t=apr
· http://www2.ucg.br/design/ da2/solidosgeometricos .pdf
Professor, para consolidar os conhecimentos teóricos visto, vamos realizar uma atividade utilizando um software de geometria dinâmica, htt p://www.geometriadinamica.com/, o Calques 3D, http://www.calques3d.org. Trata-se de um software de geometria espacial para se utilizado em ambiente de sala de aula, que dispõe de um conjunto de comandos de criação de objetos e de construção onde é possível marcar e medir ângulos, recuperar o histórico de uma construção, fazer macro-construções etc. O Calques 3D atende a um conjunto diverso de objetivos didáticos que contribuem para que os alunos desenvolvam seu pensamento geométrico, com destaque para atividades relacionadas de: Planejar – Explorar – Modelar – Conjecturar – Definir – Argumentar – Demonstrar. Esta disponível em http://www.calques3d.org/download/setup.zip. Alguns exemplos de atividades que podem ser desenvolvidas com o aplicativo estão disponíveis em http://www.calques3d.org/examples.html. No caso desta atividade, tenha instalado previamente o Calques 3D em todos os computadores do laboratório de informática. Existem alguns tutoriais, sobre o software, disponíveis em:
· Referência nacional do Calques 3D: http://www.professores.uff.br/hjbortol/calques3d/
· Calques 3D – Ponto Livre (dar nome e suprimir): http://mais.uol.com.br/view/i54gm6ahdxbb/calques-3d–ponto-livre-dar-nome-e-suprimir-0402356CD0913326?types=A&
· Calques 3D – Retas e Segmentos: http://mais.uol.com.br/view/i54gm6ahdxbb/calques-3d–retas-e-segmentos-04023966D4913326?types=A&
· Calques 3D – Paralelas e Perpendiculares: http://mais.uol.com.br/view/i54gm6ahdxbb/calques-3d–paralelas-e-perpendiculares-0402316AD4913326?types=A&
· Calques 3D – Polígonos, Circunferências e Arcos: http://mais.uol.com.br/view/i54gm6ahdxbb/calques-3d–poligonos-circunferencias-e-arcos-0402306CD4913326?types=A&
· Ponto Simétrico e Translação: http://mais.uol.com.br/view/i54gm6ahdxbb/calques-3d–ponto-simetrico-e-translacao-0402316ED4913326?types=A&
· Planos 1: http://mais.uol.com.br/view/i54gm6ahdxbb/calques-3d–planos-1-04023172D4913326?types=A&
· Planos (2) e Esfera: http://mais.uol.com.br/view/i54gm6ahdxbb/calques-3d–planos-2-e-esfera-0402356AD8913326?types=A&
· Calques 3D – Medidas, Histórico e Volume: http://mais.uol.com.br/view/i54gm6ahdxbb/calques-3d–medidas-historico-e-volume-04023466DC913326?types=A&
· Cálculo do Volume do Tetraedro: http://mais.uol.com.br/view/i54gm6ahdxbb/calques-3d–construcao-do-triangulo-equilatero-04023762DC913326?types=A&
· Construção do Triângulo Isósceles: http://mais.uol.com.br/view/i54gm6ahdxbb/calques-3d–construcao-do-triangulo-isosceles-0402326EE0913326?types=A&
· Losango,Triângulo e Trapézio Isósceles na mesma Construção: http://www.youtube.com/watch?v=coRixnKaua8
· Construção do Triângulo Equilátero: http://mais.uol.com.br/view/i54gm6ahdxbb/calques-3d–construcao-do-triangulo-equilatero-04023762DC913326?types=A&
· Atributos e Centro de Circunferência: http://mais.uol.com.br/view/i54gm6ahdxbb/calques-3d–atributos-e-centro-de-circunferencia-04023472E0913326?types=A&
· Trapézio isósceles: http://www.youtube.com/watch?v=JHWlAf3wvLI&feature=related
Professor, vamos fazer alguns estudos do cilindro utilizando o Calques 3D. Siga os seguintes passos:
Passo 1: Inicie o aplicativo. A janela com a área de trabalho é chamada de Universo.
Passo 2: Retirar as paredes da área de trabalho. Clique com o mouse no ícone  na segunda barra de ícones e selecione a opção “Nenhum”.
na segunda barra de ícones e selecione a opção “Nenhum”.
Passo 3: Acrescentado pontos.
· No menu “Objeto”, selecione a opção “Ponto” ou clique com o mouse no ícone  na segunda barra de ícones, abaixo do menu principal. Note que aparecera m as paredes para fixação dos pontos, mas logo após a fixação dos pontos, elas desaparecerão novamente. O primeiro clique a ser dado é para selecionar em qual plano será criado o ponto, clique com o mouse no plano horizontal e em seguido um segundo para fixar o ponto.
na segunda barra de ícones, abaixo do menu principal. Note que aparecera m as paredes para fixação dos pontos, mas logo após a fixação dos pontos, elas desaparecerão novamente. O primeiro clique a ser dado é para selecionar em qual plano será criado o ponto, clique com o mouse no plano horizontal e em seguido um segundo para fixar o ponto.
· Clique com o mouse no ícone  na segunda barra de ícones, abaixo do menu principal ou pressione a tecla “Esc” (Tarefa padrão) e, em seguida, clique no ponto criado. Observe que no lado direito da tela, uma janela de “Atributos”. Clique no atributo “Nome” e altere no nome para A, ou seja, criamos um ponto que se chama A. Nesta janela também podemos mudar atributos como cor, visibilidade e forma do objeto.
na segunda barra de ícones, abaixo do menu principal ou pressione a tecla “Esc” (Tarefa padrão) e, em seguida, clique no ponto criado. Observe que no lado direito da tela, uma janela de “Atributos”. Clique no atributo “Nome” e altere no nome para A, ou seja, criamos um ponto que se chama A. Nesta janela também podemos mudar atributos como cor, visibilidade e forma do objeto.
· Para exibir o nome do ponto, no menu “Exploração” selecione a opção “Rótulo” e em seguida clique no ponto A.
· Peça aos alunos que criem um ponto B e C.
Passo 4: Criar um plano que passa pelos três pontos criados. No menu “Objeto”, selecione a opção “Plano” ou clique com o mouse no ícone  na segunda barra de ícones. Clique nos pontos A, B e C, nesta ordem.
na segunda barra de ícones. Clique nos pontos A, B e C, nesta ordem.
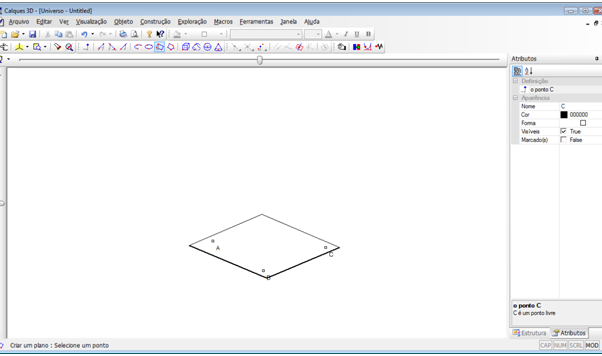
Passo 5 – Criar uma circunferência que passa pelos pontos criados. No menu “Objeto”, selecione a opção “Circunferência” ou clique com o mouse no ícone  na segunda barra de ícones. Clique nos pontos A, B e C. Altere o nome da circunferência para “BaseCilindro”.
na segunda barra de ícones. Clique nos pontos A, B e C. Altere o nome da circunferência para “BaseCilindro”.
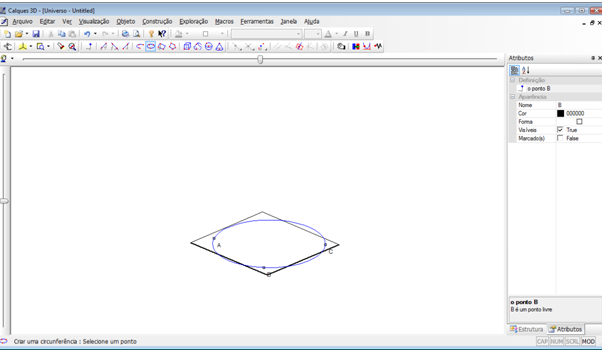
Passo 6 – Determinar o centro da circunferência. No menu “Construção”, selecione a opção “Centro de uma circunferência”. Clique na circunferência “BaseCilindro”. Altere o nome do ponto para “O” em mostre o rótulo.
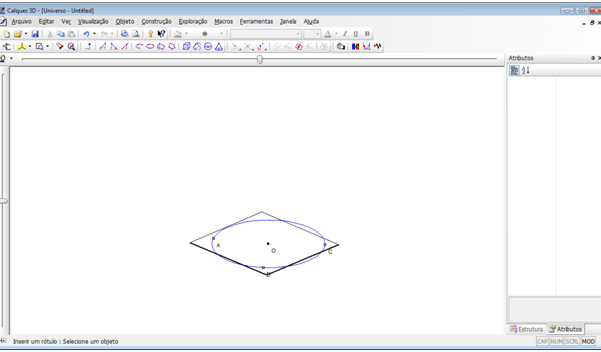
Passo 7 – Criar uma reta perpendicular ao plano criado e que passa pelo ponto O. No menu “Construção”, selecione a opção “Reta normal” ou clique com o mouse no ícone  na segunda barra de ícones. Clique no plano e em seguida no ponto “O”.
na segunda barra de ícones. Clique no plano e em seguida no ponto “O”.
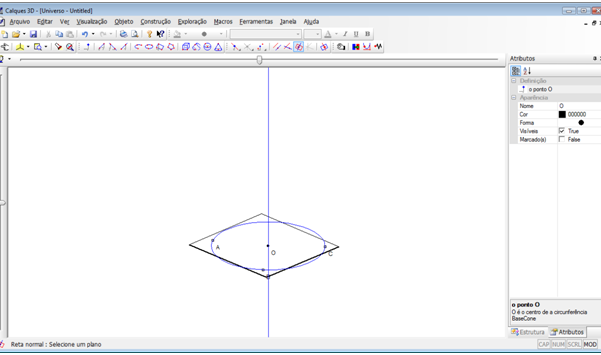
Passo 8 – Criar um ponto sobre a reta criado, que determinar o centro da base superior e a altura do cilindro. No menu “Construção”, selecione a opção “Point on” e, em seguida, em “Reta” ou clique com o mouse no ícone  na segunda barra de ícones. Clique duas vezes na reta. Altere o nome do ponto para “V”.
na segunda barra de ícones. Clique duas vezes na reta. Altere o nome do ponto para “V”.
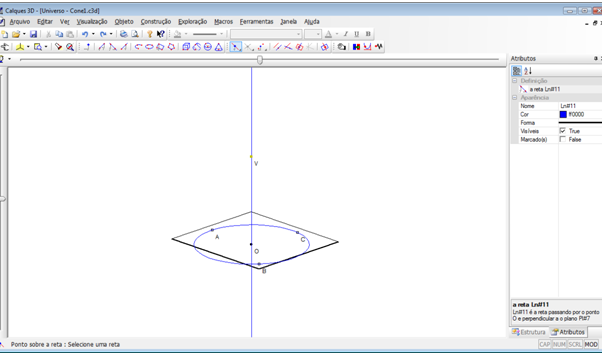
Por questões de estética, vamos esconder a linha normal criada. Podemos esconder um objeto de duas formas:
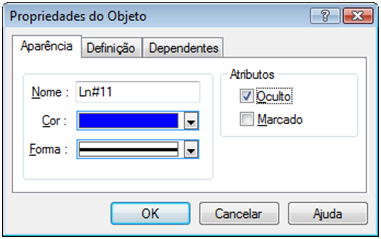
1ª forma: Dê um clique sobre a reta normal criada. Na janela “Atributos”, dê um clique duplo na propriedade “Visíveis”.
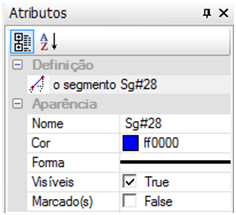
2ª forma: Dê um duplo clique sobre a linha normal criada. Aparecerá a janela de “Propriedades do Objeto”, em “Atributos”, clique em “Oculto” e depois em “Ok”.
Teremos a seguinte tela:
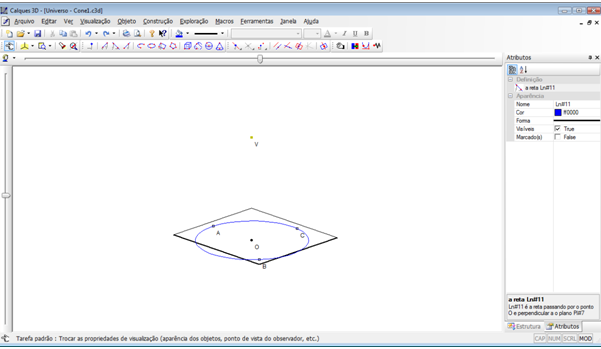
Passo 9 – Criar um cilindro. No menu “Objeto” selecione a opção “Volume” e, em seguida, a opção “Cilindro” ou clique com o mouse no ícone  na segunda barra de ícones. Clique no ponto “V”, o vértice do cone; depois no ponto “O”, centro da circunferência “BaseCone”; e por último, em um dos pontos A, B e C, pontos da base do cone.
na segunda barra de ícones. Clique no ponto “V”, o vértice do cone; depois no ponto “O”, centro da circunferência “BaseCone”; e por último, em um dos pontos A, B e C, pontos da base do cone.
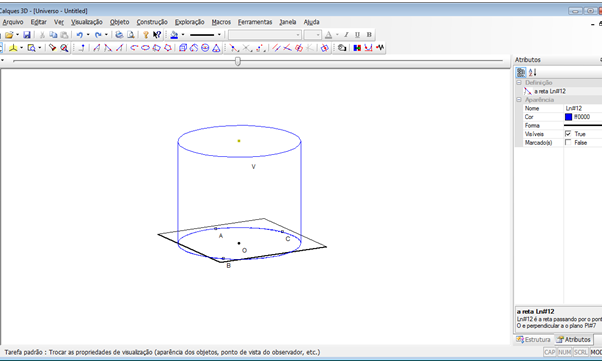
Professor, comente com seus alunos que:
· O cone criado pode ser movimentado. Clique com o mouse no ícone  na segunda barra de ícones, em seguida clique e segure em no ponto A e movimente-o. Professor, peça aos seus alunos que façam a movimentação com os outros pontos criados.
na segunda barra de ícones, em seguida clique e segure em no ponto A e movimente-o. Professor, peça aos seus alunos que façam a movimentação com os outros pontos criados.
· Abaixo da segunda barra de ícones, temos um controle deslizante,  , este controle tem a função de movimentar o objeto criado na horizontal, pode-se também utilizar um atalho pressionando as setas para direita ou para esquerda. E no lado esquerdo, outro um controle deslizante na vertical (atalho pressionando as setas para cima ou para baixo). Peça aos alunos que movimentem o objeto criado, com o intuito de ambientarem com o software.
, este controle tem a função de movimentar o objeto criado na horizontal, pode-se também utilizar um atalho pressionando as setas para direita ou para esquerda. E no lado esquerdo, outro um controle deslizante na vertical (atalho pressionando as setas para cima ou para baixo). Peça aos alunos que movimentem o objeto criado, com o intuito de ambientarem com o software.
· Podemos também movimentar toda a área de trabalho. Com a “Tarefa padrão” selecionada, pressione a tecla “Shift” e clique em qualquer local da área de trabalho e movimente-a.
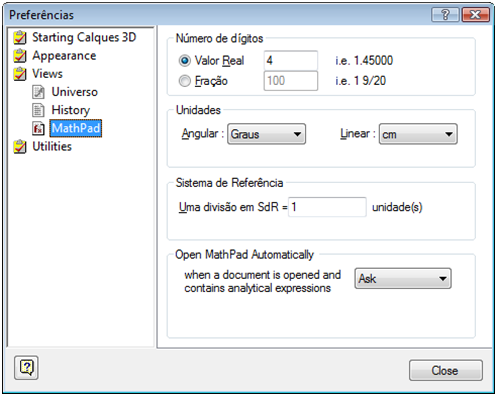
Professor, podemos configurar a precisão da quantidade de casas decimais nas operações matemática. No menu “Arquivo”, selecione a opção “Opções” e será mostrada a janela “Preferências”. No lado esquerdo da janela, no item “Views” selecione a opção “MathPad” e altere a opção “Valor Real” para 4 casas decimais; em “Unidades”, “Angular” para Graus e “Linear” para cm. Em seguida clique com o mouse em “Close”.
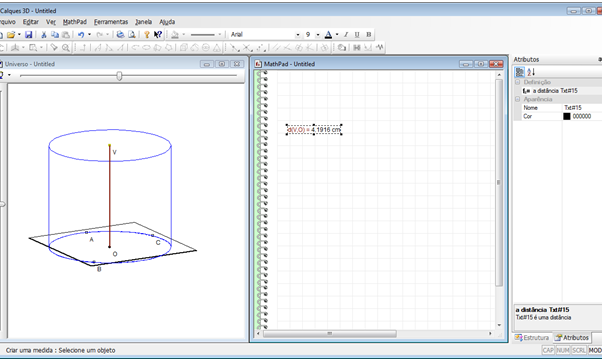
Passo 10: Medir a altura do cilindro. No menu “Exploração” selecione a opção “Medida”. Na área de trabalho, clique no botão direito do mouse e será apresentado o menu suspenso com as opções “Ângulo”, “Distância”, “Comprimento”, “Área” e “Volume”, selecione a opção “Distância” e em clique no ponto V e, em seguida, no ponto O. Será mostrada uma janela com o título “MathPad”, que funciona como uma folha de cálculo. Note que apareceu a expressão, no nosso exemplo, d(V,O) = 4.1916 cm. Professor, oriente seus alunos para clicar e arrastar a expressão para uma posição mais abaixo na janela porque a próxima expressão a ser incluída, será no mesmo local. Mostre que ao clicar na expressão criada foi mudada a cor do segmento da altura.
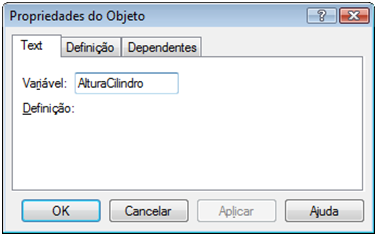
Peça a eles que cliquem com o botão direito do mouse na expressão criada. Será mostrada uma janela e nela, selecione a opção “Propriedades”. Será mostrada a janela “Propriedades do Objeto”. Em “Variáveis”, digite “AlturaCilindro” e clique em “Ok”. A respeito do nome das variáveis criadas, o Calques 3D faz diferença com nome utilizando letras maiúsculas e minúsculas, portanto tenha cuidado na definição das variáveis.
Professor, peça aos alunos que cliquem na janela “Universo”, movimente o ponto V e observe o que acontece a medida da altura do cilindro.
Passo 11: Inserindo um comentário na janela “MathPad”.
· Clicando com o botão direito do mouse em um local livre na janela “MathPad” aparecerá a janela com as opções “Inserir um comentário” e “Inserir expressão”.
· Selecione “Inserir comentário”, aparecerá um rótulo com a mensagem “novo comentário...”,
· Dê um duplo clique e altere o texto, por exemplo: “Estudo do cone”.
· Dê um clique e arraste para o local desejado.
Passo 12: Medir o raio da base do cilindro. Medir a distância do ponto O ao ponto A; atribua o nome “RaioBaseCilindro”, ver passo 10.
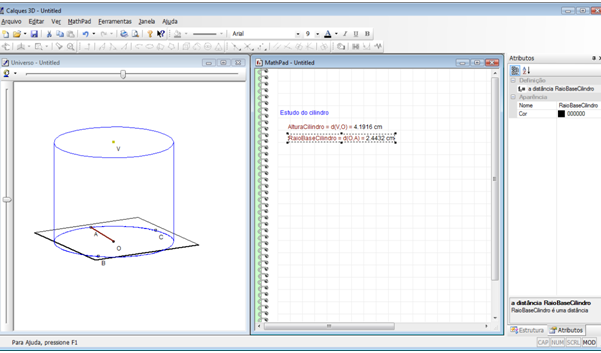
Professor, na janela “MathPad” podemos utilizar constantes, operadores e funções, conforme abaixo:
· Constantes matemáticas: E e Pi
· Operadores aritméticos: +, -, *,/
· Resto de divisão: %
· Potenciação: **
· Operações lógicas e relações: <, >, =, >, <
· Funções:
o cos (x) – retorna o valor do cosseno de x.
o sin (x) – retorna o valor do seno de x.
o tan (x) – retorna o valor da tangente de x.
o atan (x) – retorna o valor do arco tangente de x.
o asin (x) – retorna o valor do arco seno de x.
o acos (x) – retorna o valor do arco cosseno de x.
o exp (x) – retorna o valor ?
o ln (x) – retorna o valor do logaritmo neperiano de x.
o lg (x) – retorna o valor do logaritmo decimal de x.
o sqrt (x) – retorna o valor da raiz quadrada de x.
o abs (x) – retorna o valor absoluto de x.
o frac (x) – retorna a parte decimal de x
o trunc (x) – retorna a parte de inteira de x
o floor(x) – retorna o inteiro o maior que é menor do que ou igual a X
o ceil (x) – retorna o inteiro o menor que é mais grande do que ou igual a X
o round (x, precisão) – retornos um número arredondado a um número especificado de lugares decimais
o sgn (x) – retorna 1 se x > 0, -1 se x < 0 e 0 se x=0.
o neg (x) – mude o sinal de x
· Variáveis: antes de usar uma variável em uma expressão, você tem que defini-la atribuindo um nome variável a todos os valores (isto é. Distância, volume, uma outra expressão, etc.) disponíveis na vista de “MathPad”. Você pode fazer um clique duplo em um valor e ajustar o nome na caixa de diálogo. Uma vez que feita, essa variável está disponível para o uso em uma expressão. Você pode selecioná-lo pelo menu situado abaixo do campo da edição na caixa de diálogo ou apenas datilografando a. Não há nenhuma verificação automática de nomes variáveis duplicados, assim que você terá que fazê-la você mesmo.
· Observação: Extrair valores de uma equação, por exemplo: o valor da abscissa ou ordenada de um ponto da equação de uma esfera não é (ainda) possível.
Passo 13: Calcular a área da base cilindro. Podemos fazer isto de duas formas:
1ª forma: Utilizar a fórmula para calcular a área do círculo. A= πr2.
· Clicando com o botão direito do mouse em um local livre na janela “MathPad” aparecerá a janela com as opções “Inserir um comentário” e “Inserir expressão”.
· Selecione “Inserir expressão”, será acrescentada na janela uma expressão “1+1=2.0000”.
· Clique na expressão criada e em seguida, clique com o botão direito do mouse. Será mostrada uma janela e nela, selecione a opção “Propriedades”. Será mostrada a janela “Propriedades do Objeto”.
· Em “Variáveis”, digite “AreaBase1”, em “Definição” digite “Pi*RaioBaseCilindro**2”, em seguida, clique em “Ok”.
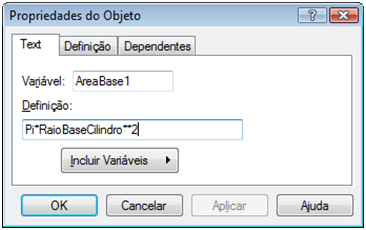
2ª Forma: Determinar a área do círculo da base do cilindro.
· Clique na janela “Universo”.
· No menu “Exploração” selecione a opção “Medida”.
· Na área de trabalho, clique no botão direito do mouse e será apresentado o menu suspenso com as opções “Ângulo”, “Distância”, “Comprimento”, “Área” e “Volume”, selecione a opção “Área” e em clique na circunferência “BaseCilindro”.
· Clique na expressão criada e em seguida clique com o botão direito e selecione “Propriedades”.
· Em “Variável” digite “AreaBase2”.
Passo 14: Calcular a área lateral do cilindro. Podemos fazer isto de duas formas:
1ª forma: Inserir uma expressão com a fórmula da área lateral do cilindro, para isto, informe “AreaLateral1” em “Variável” e em “Definição” informe “2*Pi*RaioBaseCilindro*AlturaCilindro”.
2ª forma: Determinar a área lateral do cilindro.
· Clique na janela “Universo”.
· No menu “Exploração” selecione a opção “Medida”.
· Na área de trabalho, clique no botão direito do mouse e será apresentado o menu suspenso com as opções “Ângulo”, “Distância”, “Comprimento”, “Área” e “Volume”, selecione a opção “Área” e em clique no cilindro.
· Clique na expressão criada e em seguida clique com o botão direito e selecione “Propriedades”.
· Em “Variável” digite “AreaLateral2”.
Passo 15: Calcular a área total do cilindro. Inserir uma expressão com a fórmula da área total do cilindro, para isto, informe “AreaTotal” em “Variável” e em “Definição” informe “2*Areabase1+AreaLateral1”.
Passo 16: Calcular o volume do cilindro. Podemos fazer isto de duas formas:
1ª forma: Inserir uma expressão com a fórmula do volume do cone, para isto, informe “Volume1” em “Variável” e em “Definição” informe “AreaBase1*AlturaCilindro”.
2ª Forma: Determinar a área do volume do cilindro.
· Clique na janela “Universo”.
· No menu “Exploração” selecione a opção “Medida”.
· Na área de trabalho, clique no botão direito do mouse e será apresentado o menu suspenso com as opções “Ângulo”, “Distância”, “Comprimento”, “Área” e “Volume”, selecione a opção “Volume” e em clique no cilindro.
· Clique na expressão criada e em seguida clique com o botão direito e selecione “Propriedades”.
· Em “Variável” digite “Volume2”.
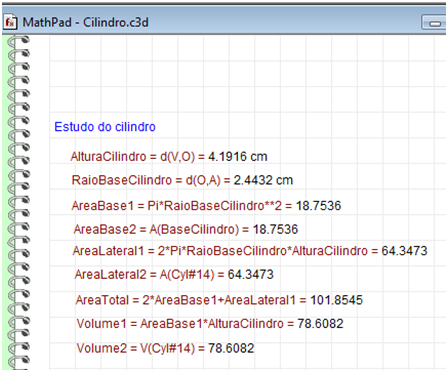
Professor, peça aos seus alunos que movimente o ponto A, B, C e V e observem os resultados na janela MathPad. Elabore também uma lista de exercícios para que os eles possam praticar um pouco, algumas listas encontram-se no sítios:
· http://www.interaula.com/matweb/gespac/cone/cone.htm
· http://broccoli.blogs.sapo.pt/919.html
· http://www.sofi.com.br/node/669
· www.escolapadrereus.com.br/material/revisao.doc
· http://www.dpedroii.com.br/apostilas/fernando/2tri/geometria_2ab.pdf
Recursos Complementares
Avaliação
A avaliação poderá ser da seguinte forma:
- Atividades em sala.
- Retomada o exercício apresentado no início da aula.
- Listas de exercícios envolvendo aplicações do assunto no cotidiano.
- Durante as aulas observando o interesse e a participação do aluno.
- Estimular os alunos a criarem e participarem de:
* Blogs sobre o assunto. Caso queira utilizar algum Blog já existente, sugerimoshttp://br.answers.yahoo.com/question/index?qid=20090923145421AA2A23V;
* Webquest, http://pt.wikipedia.org/wiki/WebQuest, sobre o assunto. Sugerimos http://www.webquestbrasil.org/criador/;
* Fórum http://www.soensino.com.br/foruns/.
- Competição entre grupos, de no máximo quatro alunos, onde cada grupo apresenta um problema outro grupo caso consiga resolvê-lo, continua na competição, caso erre, será eliminado.
- Professor experimente criar um ambiente virtual onde você e os professores poderão criar blogs, webquest, fóruns, exercícios virtuais. Acesse http://www4.escola24h.com.br/.
- Seminários: “A importância dos cilindros e suas aplicações no dia-a-dia”. O seminário será organizado em grupos de quatro alunos. Os alunos irão abordar as aplicações dos cilindros através de exercícios, cartazes, desenhos geométricos, situações problema.
Quatro estrelas 1 classificações
- Cinco estrelas 0/1 - 0%
- Quatro estrelas 1/1 - 100%
- Três estrelas 0/1 - 0%
- Duas estrelas 0/1 - 0%
- Uma estrela 0/1 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Rosilene Nóbrega, CEM 03 Gama , Distrito Federal - disse:
mell.mat@hotmail.com01/11/2015
Quatro estrelasExcelente explanação e muito rico em recursos para serem explorados em sala de aula.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


