Identificar o arco capaz como lugar geométrico
Aplicar o arco capaz , na resolução de problemas gráficos.

Propriedades de ângulo central, ângulo inscrito e de segmento.
Traçado de mediatriz

Professor, realize com os alunos o seguinte experimento: peça-lhes que desenhem no chão, com giz colorido, uma grande circunferência, tracem uma de suas cordas e determinem um ponto A no arco menor.

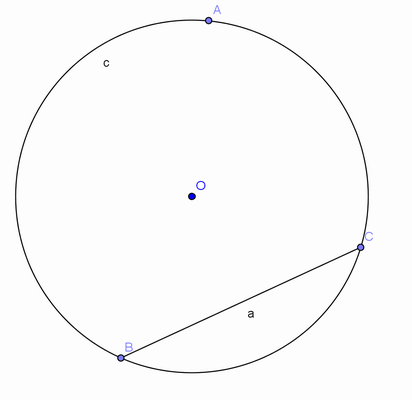
A seguir, usando dois fios de barbante esticados, solicite-lhes que tracem um ângulo inscrito de vértice em A, cujos lados passem pelas extremidades da corda que traçaram. Para medir esse ângulo, os alunos podem usar um semicírculo recortado de uma folha de cartolina, do qual recortarão a parte que corresponde o ângulo A, reservando a outra.

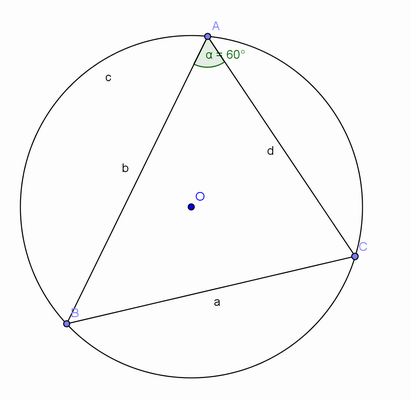
Mudando a posição do ponto A no arco menor, eles poderão comprovar que todos os ângulos têm a mesma medida.

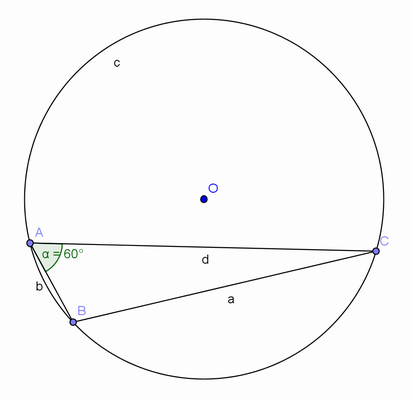
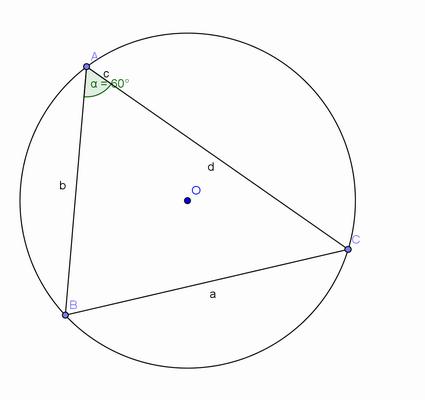
Depois, peça-lhes que repitam a experiência, agora usando o outro arco. Pretendemos que eles percebam que os ângulos (inscritos nos arcos maior e menor) são suplementares.

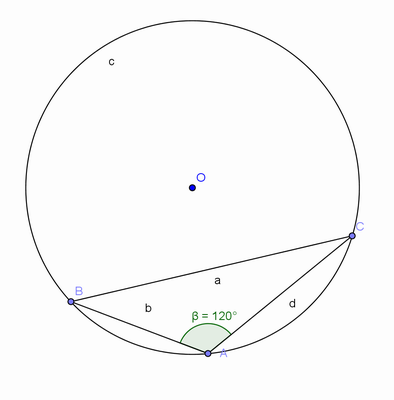
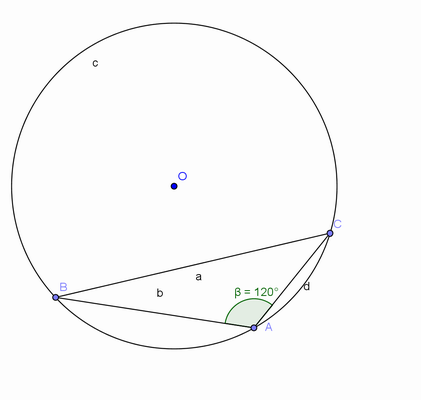
Em sala de aula, defina arco capaz como o lugar geométrico dos pontos que enxergam um segmento de reta sob um ângulo de medida constante. Estude as propriedades, que justificam a construção e faça as construções com régua e compasso.

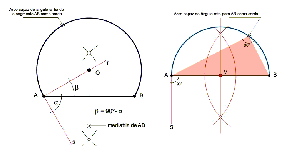
http://www.desenhoprojetivo.pro.br/htmldg/linhasproporcionais.htm

http://educacao.uol.com.br/matematica/ult1705u8.jhtm

http://www.cerescaico.ufrn.br/Construcoes_geometricas-1.pdf

Avalie a aula e os alunos por exercícios de construção e pela atividade prática, observando os seguintes aspectos:

• Elaboração de estratégias para a resolução de um problema ;
• Resolução gráfica.