04/12/2009
Fernando Celso Villar Marinho, Daniella Assemany da Guia
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Educação de Jovens e Adultos - 2º ciclo | Matemática | Proporcionalidade e Equivalência |
| Ensino Fundamental Final | Matemática | Grandezas e medidas |
| Ensino Fundamental Final | Matemática | Operações |
O que o aluno poderá aprender com esta aula
Reconhecer a proporção como a igualdade de duas razões.
Aplicar a propriedade fundamental das proporções em situações-problema.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Equivalência de frações.
Conceitos de razão e de números e grandezas proporcionais.
Resolução de equações do 1º grau.
Estratégias e recursos da aula
Como consta nos PCN (SEF/MEC, 1998), uma das considerações no bloco Grandezas e Medidas, é a importância de levar em conta as conexões das medidas com os demais blocos de conteúdos matemáticos. Ou seja: o professor, ao propor situações-problema envolvendo grandezas e medidas, proporcionará contextos para a construção de conceitos e procedimentos não só os estritamente relacionados a este tema, mas também a outros, como ampliação dos campos numéricos, razões e proporções, gráficos cartesianos, relações geométricas, medidas estatísticas etc.
O objetivo dessa aula é introduzir, através de situações-problema, o conceito de proporção, como também apresentar a propriedade fundamental da proporção.
Para uma introdução ao conceito de proporção, sugerimos que o professor convide os alunos a assistirem o vídeo com duração aproximada de 12 minutos.
 A divisão e suas interpretações [Matemática na vida]
A divisão e suas interpretações [Matemática na vida]
Acesse o link: http://portaldoprofessor.mec.gov.br/fichaTecnica.html?id=18306
Professor, sugerimos duas atividades iniciais para revisar os conceitos de razão e de números e grandezas proporcionais e, a partir das mesmas, apresentar as proporções.
Atividade 1.
Para fazer um refresco, uma pessoa mistura 2 medidas de suco concentrado em 8 copos de água.
Complete a tabela abaixo sabendo que, em todas as situações, o refresco é sempre o mesmo, ou seja, tem a mesma concentração.
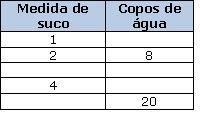
Sugestão: Dê tempo aos alunos para discutirem e completarem a tabela e, em seguida, com a participação da turma, registre na tabela:
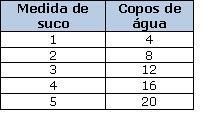
Nota: Espera-se que o aluno perceba em todas as situações que: para cada medida de suco são necessários quatro copos de água.
Proponha que eles registrem, em cada linha da tabela, a razão:
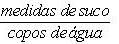
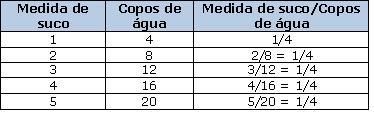
Questione os alunos se as grandezas medidas de suco e copos de água são proporcionais.
Nota: Espera-se que os alunos percebam que, como as razões obtidas são todas iguais, as grandezas são proporcionais.
Use as razões obtidas na tabela para escrever vários pares de razões iguais e apresente cada igualdade como sendo uma proporção.
Alguns pares de proporção:
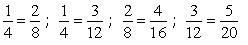
Atividade 2.
Complete a tabela a seguir, sabendo que as medidas dos lados dos quadrados Q1, Q2, Q3, Q4 e Q5 são, respectivamente, 1, 2, 4, 8 e 16 cm.
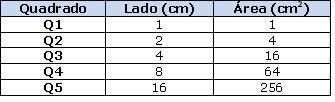
Utilize o mesmo procedimento da atividade 1 e, com a participação da turma, registre as soluções:
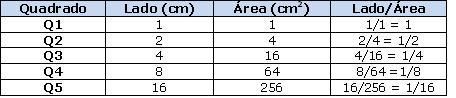
Nessa situação, as grandezas lado e área não são proporcionais.
Registre também que as razões obtidas são diferentes e, portanto, não formam uma proporção.
Exemplo:
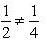
Professor, caso haja necessidade, elabore outras atividades que envolvam números ou grandezas proporcionais e não proporcionais.
Propriedade Fundamental das Proporções
Para apresentar a propriedade, sugerimos não utilizar as nomenclaturas desnecessárias “meios” e “extremos”, visto que os alunos estão familiarizados com “numerador” e “denominador”.
Utilize, por exemplo, a atividade 1 para trabalhar a propriedade através das várias proporções obtidas.
Apresente algumas proporções e proponha as multiplicações: produto do numerador da 1ª fração com o denominador da 2ª, e produto do denominador da 1ª com o numerador da 2ª fração.
Em cada proporção, faça-os observar que esses pr odutos são iguais.
Exemplos:
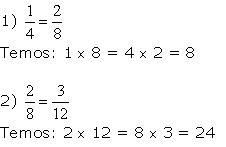
Enuncie então a propriedade:
Em toda proporção, os produtos do numerador de uma razão pelo denominador da outra são iguais.
Algumas aplicações da propriedade:
1. Utilizando a propriedade fundamental da proporção, relacione as razões com o sinal 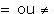
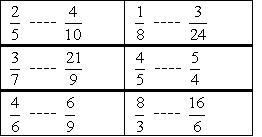
2. Em uma lanchonete, de cada 8 sucos vendidos, 5 são de laranja. Em um final de semana foram vendidos 480 sucos. Quantos destes sucos vendidos foram de laranja?
Uma solução:
sucos de laranja vendidos: x
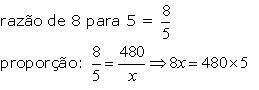
x = 300
Resposta: Foram vendidos 300 sucos de laranja.
Professor, para facilitar a sua aula, acesse o link: e tire cópias com as atividades da aula para os alunos.
Recursos Educacionais
| Nome | Tipo |
|---|---|
| A divisão e suas interpretações [Matemática na vida] | Vídeo |
Recursos Complementares
Link à folha de atividades.
Avaliação
A avaliação do aluno pode ser feita levando em consideração:
– participação em aula
– resolução de atividades em aula
– trabalhos em grupo ou individuais
– questões-desafio para serem desenvolvidas em aula
Cinco estrelas 4 classificações
- Cinco estrelas 4/4 - 100%
- Quatro estrelas 0/4 - 0%
- Três estrelas 0/4 - 0%
- Duas estrelas 0/4 - 0%
- Uma estrela 0/4 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Eremilde Lopes Bino, EEEF Antonio Carneiro Ribeiro , Espírito Santo - disse:
eremildelopes@hotmail.com16/11/2016
Cinco estrelasMaravilhosa a aula, a forma de trabalhar a matemática ficou mais prazerosa, nossos alunos estão encantados.
-
Carlos Sérgio Alves dos Santos, E.E.F Elisiário Dias , Rio Grande do Norte - disse:
carlos-sergio2@hotmail.com25/01/2015
Cinco estrelasAula Maravilha, muito bem elaborada, aborda os temas de forma suave com exemplos práticos vivenciado pelos alunos no seu cotidiano. Ótima aula.
-
maria auxiliadora telles da silva, EEEFM Pedreiras , Espírito Santo - disse:
p_reta_telles@hotmail.com10/09/2013
Cinco estrelasadorei, comecei a trabalhar este conteudo e estava necessitando deste reforço. maravilhoso
-
Francisco de Assis Lins Maciel, Escola São Luís , Pernambuco - disse:
chicoalgebra@gmail.com12/07/2010
Cinco estrelasMuito bom, nota 1000..., obrigado por colaborar com a educação em nosso país.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


