24/01/2010
Pedro Luiz Aparecido Malagutti
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Fundamental Final | Matemática | Espaço e forma |
| Ensino Médio | Matemática | Geometria |
O que o aluno poderá aprender com esta aula
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Conhecimentos básicos de Geometria Plana:
- Ângulos;
- Triângulos;
Trigonometria no Triângulo retângulo.
Estratégias e recursos da aula
Importância
Levar o aluno a usar a tangente para descobrir a altura da tabela de uma cesta de basquete.
Atividade
Professor, a sugestão é que esta atividade seja trabalhada em grupo de 3 a 4 alunos.
Exercício para entender o contexto:
Temos abaixo um esquema de uma sala de cinema, com o piso horizontal.
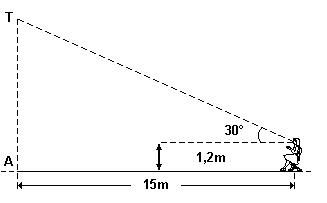
É possível calcular a distância do observador até a tela (no exemplo 15 metros) e a altura do observador (no exemplo 1,2 metros). Podemos, então, calcular a medida de AT se conhecemos o ângulo de visada de 30o da horizontal.
Discuta com seu grupo como fazer isso e apresente os seus cálculos.
Observe que nesse momento os alunos compreenderão o que é o ângulo de visada e como a trigonometria no Triângulo retângulo pode auxiliar o cálculo de medidas inacessíveis.
Vamos então fazer um experimento: Ir até o ginásio de esportes da escola (um local plano e, assim, minimiza os erros que surgem no meio do caminho) para medir a altura da tabela da cesta da basquete.
Material Necessário:
- Papel cartão;
- Régua;
- Transferidor (de meia volta);
- Tesoura;
- Calculadora;
- Canudo;
- Fita adesiva;
- Barbante;
- 2Trenas (uma de 2 metros e outra com 30 metros);
- Uma borracha para funcionar como peso;
1a Parte: Construção da ferramenta
Vamos construir um objeto rústico com a intenção de medir o ângulo de visada.
Recorte um pedaço (20cm X 10cm) do papel cartão; Trace uma reta perpendicular ao maior lado, no centro
do papel; Fixe o transferidor neste pedaço de papel usando a fita transparente e com a reta desenhada coincidindo
com o ângulo de 90º, como na abaixo; Amarre na ponta da linha (20cm) a borracha e prenda a outra extremidade no centro do transferidor usando a fita na parte de trás do papel; Prenda o canudo também com a fita adesiva na linha
de fé do transferidor.
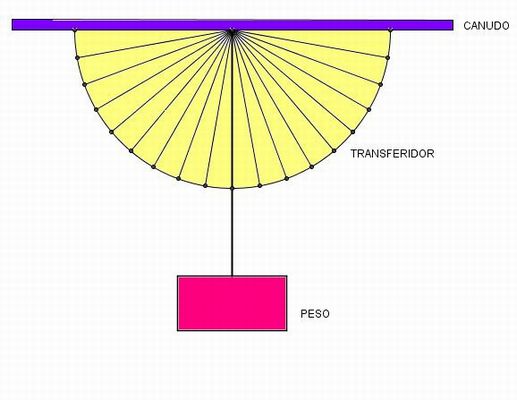
2a Parte: Procedimento:
Primeiro deve-se marcar no chão a linha perpendicular que contém a tabela. Deste ponto em diante, usar a trena maior para marcar as distâncias de 5m, 10m, 20m, 30m para serem referência de marcação.
Cada grupo deve usar a tenha menor para medir a altura da observação.
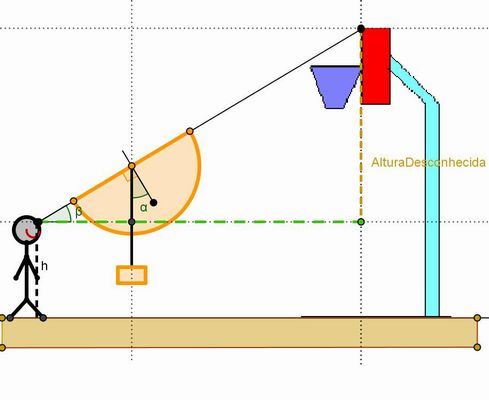
O observador deve olhar pelo canudo até mirar o ponto de referência da medição. E ver qual o ângulo alfa encontrado.
Peça para que os alunos registrem os dados obtidos em uma tabela:
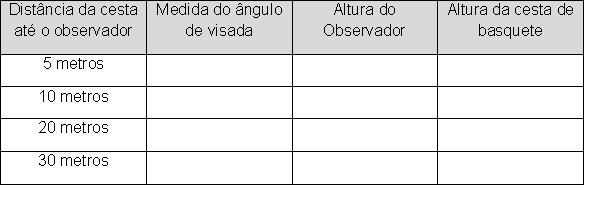
Observe que o ângulo alfa será o ângulo encontrado no instrumento e coincide com o ângulo beta que é o ângulo de visada. Explore essa coincidência com seus alunos.
Confrontem os resultados encontrados e peça para que os alunos pesquisem qual é o padrão de medida da tabela e se o valor qual a relação da eficiência do experimento.
Avaliação
Professor, para avaliar seu aluno use a própria atividade desenvolvida.
Sem estrelas 0 classificações
- Cinco estrelas 0/0 - 0%
- Quatro estrelas 0/0 - 0%
- Três estrelas 0/0 - 0%
- Duas estrelas 0/0 - 0%
- Uma estrela 0/0 - 0%
Denuncie opiniões ou materiais indevidos!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


