23/01/2010
Pedro Luiz A. Malagutti
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Fundamental Final | Matemática | Sistema de numeração decimal |
| Ensino Fundamental Final | Matemática | Números e operações |
| Ensino Fundamental Final | Matemática | Aritmética |
O que o aluno poderá aprender com esta aula
Os estudantes deverão elaborar explicações baseadas em raciocínio matemático, que usam, principalmente, a divisão.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Operações básicas.
Estratégias e recursos da aula
O texto abaixo é formado por partes do material de livre acesso do programa de Iniciação Científica Júnior da OBMEP, disponível ta,b´me no site abaixo:
http://www.obmep.org.br/export/sites/default/arquivos/Eureka.pdf
Sociedade Brasileira de Matemática
EUREKA! Edição Especial, 2007 15
PARIDADE
Eduardo Wagner
♦ Nível Iniciante.
Todo número natural é par ou ímpar.
Elementar, não? A afirmação acima, que é uma das mais simples e óbvias da Matemática, é também uma ferramenta de grande utilidade na resolução de muitos problemas envolvendo números naturais. Vamos comentar neste artigo alguns deles, em graus diferentes de dificuldade,
mas inicialmente precisamos recordar três importantes propriedades:
a) a soma de dois números pares é par.
b) a soma de dois números ímpares é par.
c) a soma de um número par com um número ímpar é ímpar.
Dizemos que dois números inteiros têm mesma paridade, quando são ambos pares ou ambos ímpares. Assim, podemos dizer que a soma de dois números inteiros é par se, e somente se, eles têm mesma paridade.
Vamos aos problemas.
PROBLEMA 1
Em um quartel existem 100 soldados e, todas as noites, três deles são escolhidos para trabalhar de sentinela. É possível que após certo tempo um dos soldados tenha trabalhado com cada um dos outros exatamente uma vez?
RESPOSTA : Não.
Escolha um soldado. Em cada noite em que trabalha, ele está em companhia de dois outros. Como 99 é um número ímpar, não podemos formar pares de soldados sempre diferentes para trabalhar
com o escolhido.
PROBLEMA 2
Um jogo consiste de 9 botões luminosos (de cor verde ou vermelha) dispostos da seguinte forma:
FIGURA 1

Apertando um botão do bordo do retângulo, trocam de cor ele e seus vizinhos (do lado ou em diagonal). Apertando o botão do centro, trocam de cor todos os seus 8 vizinhos porém ele não.
Exemplos:
Apertando 1, trocam de cor 1, 2, 4 e 5.
Apertando 2, trocam de cor 1, 2, 3, 4, 5 e 6.
Apertando 5, trocam de cor 1, 2, 3, 4, 6, 7, 8 e 9.
Inicialmente todos os botões estão verdes. É possível, apertando sucessivamente alguns botões, torná-los todos vermelhos?
RESPOSTA : Não é possível.
Observe que apertando um botão do vértice do retângulo, trocam de cor 4 botões. Apertando um botão do meio de um lado, trocam de cor 6 botões e apertando um botão do centro trocam de cor 8 botões. Assim, cada vez que apertamos um botão trocam de cor um número par de botões. Como existem 9 botões, não é possível que todos troquem de cor.
PROBLEMA 3
Escrevemos abaixo os números naturais de 1 a 10.
1 2 3 4 5 6 7 8 9 10.
Antes de cada um deles, coloque sinais “+” ou “–” de forma que a soma de todos seja zero.
SOLUÇÃO: Não é possível fazer isto.
Imaginando que fosse possível, deveríamos separar os números dados em dois grupos com a mesma soma. Então colocaríamos sinais negativos nos números de um dos grupos e sinais positivos nos números do outro.
Teríamos então uma soma igual a zero. Acontece que a soma dos números naturais de 1 a 10 é igual a 55. Como este número é ímpar, não podemos separar os números dados em dois grupos que tenham a mesma soma.
Como o leitor deve estar percebendo, os argumentos utilizados permitiram concluir que as respostas dos três problemas propostos foram iguais: “não é possível fazer tal coisa”. Na maioria das vezes, um argumento de paridade serve exatamente para isto. Mostrar que um determinado fato não pode ocorrer e isto não é desanimador, muito pelo contrário. Serve para nos convencer que não adianta ficar gastando tempo demais fazendo tentativas inúteis. As experiências são valiosas no sentido de nos abrir os olhos para a possibilidade do problema não ter solução e, a partir daí, buscar um argumento que resolva definitivamente a questão.
É muito importante também explorar um problema, ou seja, imaginar pequenas modificações no enunciado e verificar o que ocorre com sua resposta. Por exemplo, o problema 3 não tem solução porque a soma dos naturais de 1 até 10 é 55 (ímpar). O que ocorreria se a soma
fosse par? Este é um novo e atrativo problema. Vamos enunciá-lo:
PROBLEMA 3A:
Escrevemos abaixo os números naturais de 1 a 11.
1 2 3 4 5 6 7 8 9 10 11
Antes de cada um deles, coloque sinais “+” ou “–” de forma que a soma de todos seja zero.
SOLUÇÃO:
A soma dos números naturais de 1 a 11 é 66. Como podemos separá-los
em dois grupos de soma 33? Começando pelos maiores observe que 11 + 10 + 9 = 30. Logo, 11 + 10 + 9 + 3 = 33. O problema 3A tem como uma solução possível:
+1 + 2 – 3 + 4 + 5 + 6 + 7 + 8 – 9 – 10 – 11 = 0
Fica ao encargo do leitor mostrar que sempre que a soma dos naturais de 1 até n é par então podemos separá-los em dois grupos de igual soma. Você pode utilizar o caminho que utilizamos acima, ou buscar uma outra forma.
Para saber mais e intrigar seus colegas Você pode propor aos seus amigos os problemas 3 ou 3A com uma lista grande de números naturais consecutivos. O problema terá ou não
solução caso a soma desses números seja par ou ímpar, respectivamente. Entretanto, é possível encontrar o resultado desta soma rapidamente, sem precisar somar todas as parcelas. A soma de todos os naturais de 1 até n é igual a ((1 + n)n)/2 . Por exemplo, a soma de todos os naturais de 1 até 10 é 55.
Procure demonstrar este fato e, se não conseguir, pergunte ao seu professor ou escreva para a EUREKA!
PROBLEMA 4
Mostre que se a, b e c são inteiros ímpares, a equação ax² + bx + c = 0 não tem raiz racional.
Comentários:
1) Um número é raiz de uma equação dada se quando for substituído no
lugar do “x” a igualdade ficar correta. Por exemplo, x = 2/3 é raiz ou solução) da equação 3x − 2 = 0 porque 3(2/3) – 2 = 0
Ainda, x = 2 é solução da equação x^4 − x³ + x −10 = 0 porque 2^4 − 2³ + 2 −10 = 0 .
Freqüentemente não sabemos como resolver uma equação mas, em geral, podemos verificar se um certo valor de x é ou não uma de suas raízes.
2) Um número é racional quando puder ser escrito como uma fração de numerador e denominador inteiros. Por exe mplo, 2/7 e 4/1 são exemplos de números racionais.
3) Quando desejamos demonstrar que certo fato é impossível utilizamos freqüentemente o método da redução ao absurdo. Este método consiste em imaginar o contrário, ou seja, que tal fato seja possível. A partir daí procuramos chegar a uma contradição, a um absurdo. Conseguindo isso,
teremos mostrado que nossa hipótese (a do contrário) é falsa e conseqüentemente, que a afirmação inicial é verdadeira.
Vamos ver tudo isso na solução do problema. Não se preocupe se você ainda não sabe resolver uma equação do segundo grau. Isto não será necessário. Tudo o que precisamos é verificar se um número racional pode ser uma raiz.
Solução do problema 4
Imaginemos que o número racional p/q seja raiz da equação ax² + bx + c = 0 onde a, b e c são inteiros ímpares. Logo, fazendo a substituição, devemos ter,
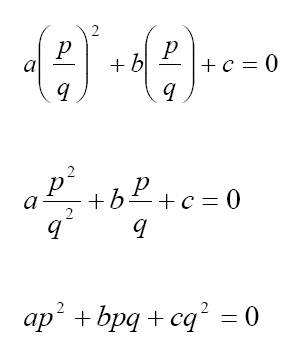
FIGURA 2
Vamos acrescentar agora uma hipótese importante para facilitar nosso trabalho. Vamos supor que a nossa fração p/q seja irredutível, ou seja, que ela já foi simplificada ao máximo. Por exemplo, no lugar de 4/6 estaremos considerando 2/3 o que é a mesma coisa. Consideramos então, para a solução do problema, que p e q não são ambos pares.
Observe agora a equação ap2 + bpq + cq2 = 0 nos seguintes casos:
a) p e q são ímpares: neste caso, ap² é ímpar, bpq é ímpar e cq² é ímpar.
Como a soma de três números ímpares é ímpar, o resultado não pode ser zero.
b) p é par e q é ímpar: neste caso, ap² é par, bpq é par e cq² é ímpar.
Como a soma de dois números pares e um ímpar é ímpar, o resultado não pode ser zero.
c) p é ímpar e q é par: vale o mesmo argumento do caso b).
Demonstramos então que nenhuma fração de numerador e denominador inteiros pode ser raiz da equação ax² + bx + c = 0 onde a, b e c são inteiros ímpares.
PROBLEMA 5
Um tabuleiro 6 × 6 está coberto com dominós 2 × 1. Mostre que existe uma reta que separa as peças do tabuleiro sem cortar nenhum dominó.
SOLUÇÃO:
Cada dominó é formado por dois quadrados e portanto, se o tabuleiro está inteiramente coberto, 18 dominós foram utilizados. Imagine agora uma reta (horizontal, por exemplo) que separe o tabuleiro em duas partes. Se ela não corta nenhum dominó, está resolvido o problema. Suponha então
que ela corte ao meio um dominó. Neste caso, acima desta reta teremos n dominós inteiros mais meio dominó, ou seja, teremos acima desta reta 2n + 1 quadrados, que é um número ímpar. Mas isto é impossível porque se o tabuleiro tem 6 unidades de largura, qualquer reta o dividirá em
partes que contém números pares de quadrados acima e abaixo dela.
Assim, se uma reta corta um dominó, deverá cortar um outro dominó.
Para a divisão do tabuleiro, existem 10 retas possíveis e, se cada uma
delas cortar dois dominós, deveríamos ter 20 dominós no tabuleiro.
Como eles são apenas 18 então existe uma reta (pelo menos) que não corta nenhum dominó.
Problemas para pesquisa
PROBLEMA 6
Os números naturais de 1 até 1998 são escritos em um imenso quadro negro. Em seguida, um aluno apaga dois quaisquer colocando no lugar sua diferença (não negativa). Depois de muitas operações, um único número ficará escrito no quadro. É possível que esse número seja zero ?
PROBLEMA 7
Em uma ilha plana existem 11 cidades numeradas de 1 a 11. Estradas retas ligam 1 a 2, 2 a 3, 3 a 4, ..., 10 a 11 e 11 a 1. É possível que uma reta corte todas as estradas?
Nem todos os problemas acima citados são acessíveis aos alunos de ensino fundamental, mas as ideia podem ser discutidas e resolvidas em conjunto com a classe e o professor!
Recurso: “Odd Number Theorem”
Este recurso educacional permite a verificação de alguns exemplos de um resultado bastante importante na Teoria dos Números.
Os estudantes podem ser convidados a explorar o recurso tentado obter uma generalização.
Este objeto requer um programa para sua visualização, portanto, baixe-o neste link do Banco Internacional de Objetos Educacionais – MathematicaPlayer
Recursos Educacionais
| Nome | Tipo |
|---|---|
| Odd number theorem | Animação/simulação |
Recursos Complementares
Revista do Professor de Matemática – SBM - http://www.ime.usp.br/~rpm/cms/
Olimpíadas Brasileiras de Matemática das Escolas Públicas -http://www.obmep.org.br
Avaliação
Recolher as resoluções de alguns problemas propostos.
Sem estrelas 0 classificações
- Cinco estrelas 0/0 - 0%
- Quatro estrelas 0/0 - 0%
- Três estrelas 0/0 - 0%
- Duas estrelas 0/0 - 0%
- Uma estrela 0/0 - 0%
Denuncie opiniões ou materiais indevidos!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus



