12/08/2009
Pedro Luiz Aparecido Malagutti
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Tecnologia para a matemática |
| Ensino Médio | Matemática | Geometria |
| Ensino Fundamental Final | Matemática | Grandezas e medidas |
O que o aluno poderá aprender com esta aula
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Ângulos.
Circunferências.
Estratégias e recursos da aula
Importância:
Levar o aluno a observação de regularidades em Geometria, a construir objetos usando o computador e, ainda, fazer demontração de um conteúdo matemático.
Conteúdo no dia a dia
O conceito desta aula - ângulos inscritos na circunferência - não é de fácil visualização no dia a dia, porém, o seu conhecimento, principalmente com o enfoque desta aula, promove o desenvolvimento de algumas habilidades que serão úteis a nossos alunos no processo de capacitação até mesmo profissional:
- O aluno irá notar a existência de situações que ao variar um dos parâmetros o resultado final permanece constante.
- O conhecimento do software GeoGebra estimula a critatividade do aluno para construir seus próprios objetos necessários, e para isso, irá utilizar muita Matemática;
- O contato com a tecnologia.
Motivação
Professor, use um objeto de aprendizagem que mostre a relação entre um ângulo inscrito e um ângulo central, para que isso possa ser estimulado ao estudo no momento seguinte.
- Sugestão: o Applet, que pode ser encontrado no site do MEC:
http://objetoseducacionais2.mec.gov.br/handle/mec/5138
Observe que no fim da página existe um arquivo que pode ser facilmente baixado. É necessário instalar o programa do MathematicaPlayer. Este é um software gratuito também disponível no site do MEC:
http://objetoseducacionais2.mec.gov.br/handle/mec/4737
Observe que é possível movimentar os pontos laranjas e as medidas dos ângulos aparecem constantes logo acima da circunferência.
Observação: Neste momento só estamos procurando a curiosidade para a proposta desta aula.
Atividade
A Teoria desta aula está muito legal no site:
http://www.cdb.br/prof/arquivos/19224_20090514120847.na%20circ
Ou ainda,
http://www.malhatlantica.pt/mat/angulos_1.htm
Isso, porque, ao apresentar os nomes de entes geoméricos, o professor clica em cima do nome e ele aparece na circunferência, dando movimento à aula.
Depois da teoria dada, por que não deixarem os alunos construirem o próprio objeto???
Vamos para a sala de informática da escola.
A construção do próprio objeto
Peça para os alunos, no laboratório de informática, abrirem o programa geogebra. Este é um software gratuito que pode ser facilmente baixado no Banco Internacional do MEC no endereço:
http://objetoseducacionais2.mec.gov.br/handle/mec/3538
Depois de baixá-lo, o professor deve instalar este programa em cada um dos computadores.
Então, siga o seguinte roteiro:
1 - Abra um Arquivo do GeoGebra.
2 - Use a ferramenta "Círculo definido pelo centro e um de seus pontos" e desenhe um círculo. Observe que irá aparecer automaticamente o ponto A como centro e um ponto B na circunferência, de tal forma que AB seja seu raio.
3 - Vamos desenhar mais três pontos C, D e E na circunferência. Para isso use a ferramenta "Novo ponto" e vá com a flecha em cima da circunferência e, clique em três lugares distintos dela para desenhar os pontos C, D e E . Estes pontos devem ser de um tom de azul mais claro que os pontos A e B, isto acontece porque eles possuem a propriedade de pertencerem à circunferência definida. Desta forma, você pode conferir isso usando a ferramenta "Mover" e movimentar estes pontos. Observe que por mais que você mexa, eles continuaram na circunferência.
4 - Vamos traçar o ângulo inscrito CED e o ângulo central CAD. Para isso, utilize a ferramenta "Segmento definido por dois pontos" e trace os segmentos AC, AD, CE e DE. Para que apareça a medida destes ângulos, use a ferramenta "Ângulo" e selecione três pontos: Primeiro C, E e D, em seguida, o ângulo C, A e D.
5 - Ajuste o ponto C de for ma que o ângulo CAD se ja fácil de calcular a sua metade, por exemplo, 62,6 graus. Você vai perceber que o programa não permite que você escreva todos os ângulos desejados.
6 - Ao final destas etapas, você e seus alunos terão uma figura parecida com:
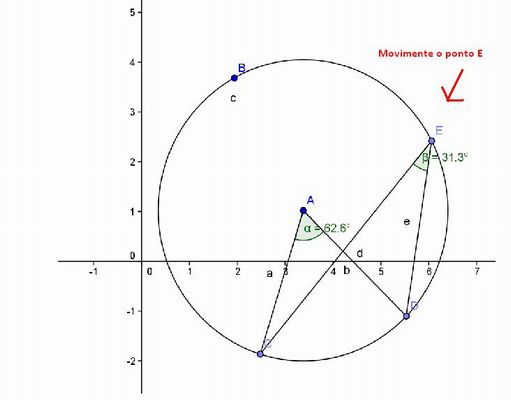
Movimente o ponto E usando a ferramenta "Mover" e observe que a medida do ângulo CED continua sempre sendo 31,3 graus (quando "enxerga" o arco de 62,6 graus), ou então, 211,3 graus (o replemento de 148,7 graus de quando o ângulo inscrito "enxerga" o arco de 297,4 graus).
Dep ois, deixe os alunos movimentarem os outros pontos e observarem as reguraridades.
O Momento Matemática Pura: A Demonstração!!!
Para formalizar a teoria vista faça a demonstração em lousa do fato observados nos experimentos feitos.
Recursos Complementares
http://www.labmat.com.pt/index.php?option=com_content&task=view&id=65&Itemid=78.
http://pessoal.sercomtel.com.br/matematica/geometria/geom-circ/geom-circ.htm
Avaliação
O professor deve usar as produções feitas pelos alunos durante as atividades.
Três estrelas 1 classificações
- Cinco estrelas 0/1 - 0%
- Quatro estrelas 0/1 - 0%
- Três estrelas 1/1 - 100%
- Duas estrelas 0/1 - 0%
- Uma estrela 0/1 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
gabriela regina de souzacosta, cba , Mato Grosso - disse:
gabisouza18@hotmai.com24/03/2010
Três estrelasfalta mais informaçoes sobre a propria matematica e tem que dar + exemplos ;mais eu gostei do mesmo jeito;obrigado me fez um favorzão;valeu!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


