04/05/2009
Marcos Paim, Eziquiel Menta
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Álgebra |
| Ensino Médio | Matemática | Números e operações |
O que o aluno poderá aprender com esta aula
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Estratégias e recursos da aula
Como as bactérias não são visíveis à olho nú, a maioria das pessoas esquecem que elas existem. Muito além de banheiros e corrimões de escadas em locais públicos, elas também estão nos teclados e mouses de computadores. Nesses locais, de acordo com pesquisas publicadas em revistas e jornais, são encontradas mais bactérias do que em um vaso sanitário ou uma sola de sapato. Gripes e diversas infecções podem ser transmitidas pelo uso desses equipamentos.
Em laboratórios, onde são realizados exames envolvendo bactérias, o crescimento da população de bactérias pode ser descrito matematicamente. Um dos objetivos desta aula é mostrar que a matemática pode ser usada para representar o crescimento das bactérias.
Para entender um pouco mais sobre as bactérias, sugerimos que o professor disponibilize para uso dos alunos o objeto de aprendizagem disponível no Portal do Professor.
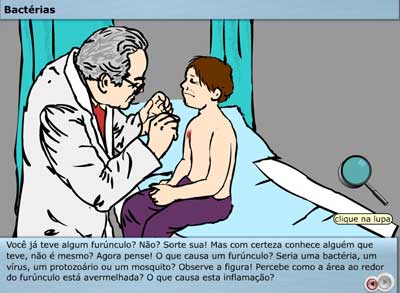
Fig. 1 - Imagem do Objeto de Aprendizagem
Recurso disponível em: http://portaldoprofessor.mec.gov.br/storage/recursos/9936/bacteria.swf
A matemática das bactérias
Sabe-se que sob certas condições em laboratório, o crescimento da população de bactérias duplica em intervalos regulares e a taxa de crescimento aumenta exponencialmente (20, 21, 22, 23,..., 2n) onde n é o número de gerações. Portanto temos uma situação real que pode ser representada matematicamente.
Esse momento é adequado para que o professor apresente a definição da função exponencial ao alunos.
A função exponencial é definida por f(x)= ax , com a pertencendo aos números reais e diferente de zero.
Também é importante ressaltar que é comum encontrarmos gráficos dessa função representando situações do cotidiano ou representando situações encontradas na natureza, muito além do crescimento populacional das bactérias.
Nessa aula os alunos devem usar a planilha eletrônica Calc/BrOffice (http://www.broffice.org) para produzir gráficos desse tipo de função. Essa é uma abordagem diferenciada que permite aprender sobre a função utilizando um recurso manipulado pelos próprios aprendizes.
Partiremos de uma situação que envolve a crescimento de uma população inicial de 12 bactérias que se duplicam a cada hora. Após 10 horas, qual seria o número de bactérias?
O primeiro passo é trabalhar com os alunos como essa situação pode ser descrita por uma função. Essa é geralmente a parte mais difícil do trabalho. É interessante notar que esse tipo de trabalho pode ser feito com outros conteúdos da matemática.
Na situação descrita anteriormente, a base exponencial é 2, pois há duplicação de quantidade de bactérias. Logo, a função pode ser escrita como f(t)= 12.2t . Feito isso, pode-se partir para o trabalho com a planilha.
Primeiro cria-se uma tabela com duas colunas e na coluna das bactérias, escreve-se a fórmula encontrada anteriormente usando a linguagem da planilha eletrônica. O resultado , 12, é apresentado imediatamente.
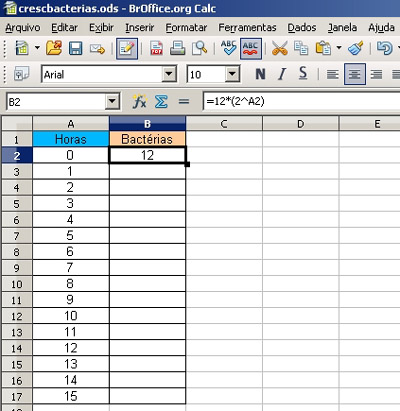
Fig. 2 - Tabela para cálculo da função.
Após aplicar a fórmula aos demais valores do tempo, é preciso selecionar as colunas e clicar no botão  que fica na parte superior do programa. Teremos então a tela de configuração do gráfico e algumas opções que podem ser escolhidas pelos alunos.
que fica na parte superior do programa. Teremos então a tela de configuração do gráfico e algumas opções que podem ser escolhidas pelos alunos.
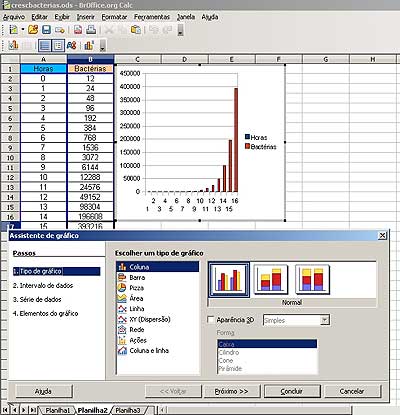
Fig. 3 - Opções para produção do gráfico.
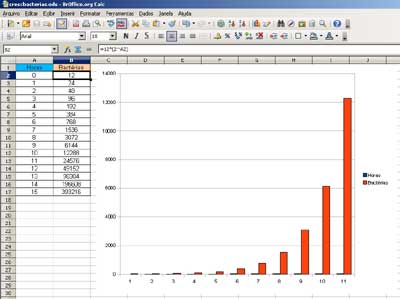
Fig. 4 - Gráfico da função.
Os cálculos do problema foram feitos automaticamente e em 10 horas, a quantidade de bactérias deve chegar a 12288. Porém o processo de interpretação do problema e criação da função não pode ser automatizado e oferecem possibilidades diferenciadas de aprendizagem usando a tecnologia.
O professor pode dar sequência ao trabalho e preparar alguns desafios para os alunos resolverem com o auxilio da planilha eletrônica. Por exemplo:
O número de bactérias de uma cultura cresce aproximadamente segunda a função f(t) = 2000. 30,006t , sendo t medido em dias.
Qual o número de bactérias no início do experimento? Em quantos dias o número inicial de bactérias irá triplicar? A partir do trabalho anterior os alunos possivelmente enxergarão na função muitas informações a respeito da situação apresentada.
Recursos Educacionais
| Nome | Tipo |
|---|---|
Recursos Complementares
Avaliação
Quatro estrelas 5 classificações
- Cinco estrelas 4/5 - 80%
- Quatro estrelas 1/5 - 20%
- Três estrelas 0/5 - 0%
- Duas estrelas 0/5 - 0%
- Uma estrela 0/5 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Josane Marcante , Colégio Dr. Mário A. T. de Freitas , Paraná - disse:
josane-cristina@bol.com.br22/07/2015
Cinco estrelasAdorei essa aula! Contextualizada e bem estruturada... Parabés!
-
GABRIELA, UEPA , Pará - disse:
gaby18braga@gmail.com23/10/2012
Quatro estrelasprático e bem legal essa aula
-
RENILEIDE FERREIRA LIMA, EE MAESTRO FREDERICO LIEBERMANN , Mato Grosso do Sul - disse:
leda.fer9@hotmail.com24/03/2010
Cinco estrelasEssa é uma aula bem diferenciada que além de trabalhar a interdisciplinaridade incluindo o uso de várias tecnologias, trabalha a matemática de forma real, em que os alunos colocam em prática e conseguem assimilar o uso da matemática como uma prática na resolução de problemas.
-
Simone, Escola , Mato Grosso do Sul - disse:
sisfer_simone@yahoo.com.br24/03/2010
Cinco estrelasMuito interessante; uma atividade para utilizar a STE.
-
ana maria paias, Governo Estado de São Paulo , São Paulo - disse:
anamariapaias@yahoo.com.br24/03/2010
Cinco estrelasAdequada a idéia de trabalhar exponencial a partir de um programa que associa gráficos.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


 Bactérias
Bactérias