23/06/2009
Eziquiel Menta
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Geometria |
| Ensino Fundamental Final | Matemática | Álgebra |
| Ensino Médio | Matemática | Álgebra |
O que o aluno poderá aprender com esta aula
- Apresentar os diferentes padrões e regularidades para desenhos que formam fractais.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Estratégias e recursos da aula

Nuvens não são esferas, montanhas não são cones, continentes não são círculos, um latido não é contínuo e nem o raio viaja em linha reta.
Benoit Mandelbrot
A Geometria Fractal pode ser usada para descrever diversos fenômenos da natureza. A Geometria tradicional - Euclidiana não dá conta de representar muitos destes fenômenos. O uso da Geometria Fractal oportuniza a apresentação de estruturas complexas e de beleza infinita, ligadas as formas da natureza, ao desenvolvimento da vida e à própria compreensão do Universo.
O trato e pesquisa dessa geometria se fortalecesse no século XIX, mesmo tendo algumas indicações e registros na Grécia Homérica, Índia, China, entre outros, mas somente há poucos anos vem se consolidando com o desenvolvimento dos computadores e o auxílio de novas teorias nas áreas da física, biologia, astronomia, matemática e outras.
Os fractais receberam este nome no início dos anos 80 por Mandelbrot, considerado o "Pai dos fractais". Existem duas características muito freqüentes nesta geometria a auto-semelhança e complexidade infinita.
Distante do rigor e do formalismo matemático, pode-se definir Fractais, como nos ensinam alguns estudiosos da área, objetos que apresentam auto-semelhança e complexidade infinita, ou seja, têm sempre cópias aproximadas de si mesmo em seu interior.
Em MENEZES (2003), encontramos que existem dois tipos de fractais: os geométricos (determinísticos) e os não-lineares (ou aleatórios). Os fractais geométricos ou determinísticos são gerados a partir de reproduções exatas de si mesmo em menor escala. Apesar de suas características especiais, os objetos fractais descritos determinísticos não permitem descrever inteira ou adequadamente as formas existentes na natureza. Já os fractais aleatórios, raramente exibem auto-semelhança exata, contudo quase sempre apresentam a chamada auto-semelhança estatística. Esta nova classe recebeu a denominação de fractais não-determinísticos e diferem dos anteriores por incluir certo grau de aleatoriedade no cálculo dos novos pontos.
Vamos aprender mais sobre fractais.
Professor apresente o vídeo, "Fractais" a seguir aos alunos e promova posterior discussão, verificando se perceberam se nestes há a auto-semelhança, se necessário retorne e pause em determinados trechos.
Disponível em: http://www.youtube.com/watch?v=WpJIp6xfUFQ
O que diferencia a Geometria de Fractais da Euclidiana?
Euclides, matemático grego, fixou seus estudos e pesquisa em provar, matematicamente, que as formas da natureza podiam ser reduzidas a formas geométricas simples, como cubos e esferas. Concentrado nas formas não considerou a dimensão presente nas formas da natureza, como no grão de areia que havia analisado anteriormente (um grão de areia apresenta três dimensões largura, altura e profundidade) enquanto que, visualmente a superfície da praia é plana, ou seja possui apenas duas dimensões.
Beroit Mandelbrot considerou as dimensões, descrevendo a ideia de Euclides matematicamente, surgindo a denominação de Fractais:
A palavra fractal do adjectivo em latim fractus o verbo latino correspondente Frangere significa “quebrar”: e para além de significar “quebrado” ou “partido” fractus também significa “irregular”. Os dois significados estão preservados em fragmento.
Semelhança e Iteração
Como construir um fractal?
Existem softwares que podem ser utilizados para construção de fractais, como podemos verificar no artigo de Rinaldi e Menezes, que é referenciado nos Recursos complementares.
Vamos optar aqui, por apresentar uma breve análise, de um dos fractais mais conhecidos, Floco de Neve de Koch.
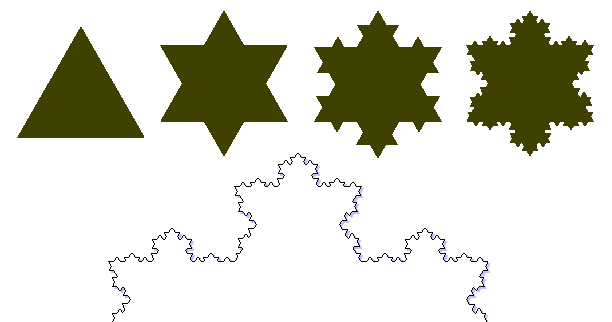
Imagem disponível em: http://www.educ.fc.ul.pt/icm/icm99/icm43/exempl_f.htm
Observando, a imagem anterior, em papel quadriculado, concluimos que:
1º : O número de lados é quatro vezes maior que o anterior.
2º : O comprimento dos lados é 1/3 do anterior.
3º : O perímetro vai aumentando à medida que aumentam as iterações*.
Colocando numa tabela, temos:
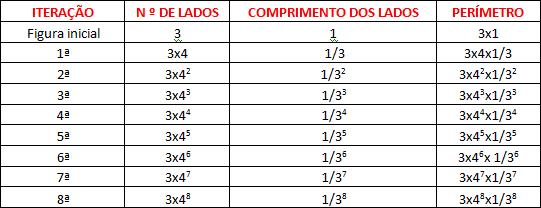
Disponível em: http://web.educom.pt/~pr2003/webquest/fractais/susana.pdf
* Iteração: processo de repetição - repetição de uma fórmula com realimentação. Para fazer um fractal escolhemos uma figura geométrica, como por exemplo, um triângulo e marcamos os pontos médios e em seguida ligamo-los; daí resultam (neste caso) três triângulos semelhantes. Em cada uma dessas três marcam-se e juntam-se novamente os pontos médios e vai-se repetindo quantas vezes se quiser. No fim cada uma das iterações todos os triângulos existentes são semelhantes entre si e ao original.

Agora é com os alunos:
Atividades em duplas:
A auto-semelhança é a propriedade que os fractais têm de as suas iterações ou gerações serem semelhantes entre si e para com o original. Um exemplo desta propriedade é o famoso triângulo de Sierpinski. Na natureza há o exemplo da couve-flor: quando se observa um “ramo” verifica-se que este é semelhante à couve-flor original.
- Em duplas, no laboratório de informática, solicite aos alunos que pesquisem:
- sobre o triângulo de Sierpinski e construam uma tabela similar a construída para o "Floco de Neve".
- outros fractais, no mínimo 3, e destes escolham 1 para refazer a tabela anterior
- Em sala de aula, ainda em duplas, encontrem a propriedade de auto-semelhança no fractal "Floco de Neve" em dois dos fractais pesquisados e, registrem, por meio de desenho a semelhança encontrada.
Atividade individual:
- O que diferencia a Geometria dos Fractais do que ocorre quando construímos caleidoscópios, como o apresentado no recurso a seguir?
- Alguma das propriedades dos Fractais (Iteração e Semelhança) podem ser aplicadas ou estão presentes na construção de caleidoscópios? Descreva em uma lauda suas conclusões.
Recursos Educacionais
| Nome | Tipo |
|---|---|
| Gaiola Prismática | Vídeo |
Recursos Complementares
- Artigo: Fractais: Uma nova visão da natureza, de Osame Kinouchi. Disponível em: http://www.ceticismoaberto.com/ciencia/kinouchi_fractais.htm. Acesso em 02 de abr. 2009.
- Artigo: Geometria fractal: análise de softwares gráficos educacionais. Por, Rinaldi, Ricardo Mendonça e Menezes, Marizilda dos Santos. Disponível em: http://www.degraf.ufpr.br/artigos_graphica/GEOMETRIAFRACTALANALISE.pdf
- Artigo: Formas geométricas e estruturas fractais na cultura africana e afrodescendentes , Por, Menezes, M. S., Cunha, JR, H. A. In: De Preto a Afrodescendente: trajetos de pesquisa sobre o negro, cultura negra e relações étnico-raciais no Brasil ed.São Carlos: EduFSCar Editora da Universidade Federal de São Carlos, 2003, p. 307-320.
- Glossário - Fractais. Disponível em: http://inforum.insite.com.br/fractais/glossarium/.Acesso em 18 de abr. 2009. - WebQuest - A magia dos fractais . Disponível em: http://web.educom.pt/~pr2003/webquest/fractais/index.htm
Avaliação
Quatro estrelas 2 classificações
- Cinco estrelas 1/2 - 50%
- Quatro estrelas 0/2 - 0%
- Três estrelas 1/2 - 50%
- Duas estrelas 0/2 - 0%
- Uma estrela 0/2 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
sandra, faculdade de filosofia ciencias e letras fundação santo andre , São Paulo - disse:
sandracristinadamata@hotmail.com15/06/2010
Cinco estrelasmuito bom o trabalho desenvolvido
-
carlos , unema t , Mato Grosso - disse:
cafsmt@bol.com.br24/03/2010
Três estrelasmelhorar nas explicaçoes teoricas.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


 Gaiola Prismática
Gaiola Prismática