Conhecer e utilizar o plano de Argand Gauss para números complexos, o módulo, o argumento e a forma trigonométrica desses números.

Duas aulas de 50 minutos cada.

O conjunto dos números reais, equações de 2º grau e alguns conceitos ligados a números complexos, sendo estes: a forma algébrica, o conjugado, as operações com esses números e as potências de i.

Sala de aula:

Para iniciar a aula, o professor pode propor aos seus alunos uma leitura dinâmica do texto “História dos números complexos” presente no endereço eletrônico:
http://www.ime.usp.br/~martha/caem/complexos.pdf.
Proponha a atividade de forma que todos leiam trechos do texto e participem. Você pode enfatizar trechos do texto que considere mais relevantes ao que será proposto durante a aula.
Em seguida, peça aos seus alunos que montem em seus cadernos um plano cartesiano e que representem valores para números complexos.

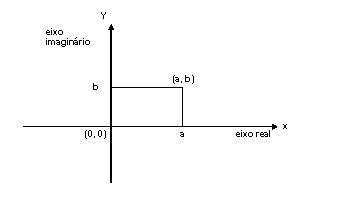
Você pode guiá-los através das perguntas:
1. Conforme visto no texto, como representamos a parte real de um número complexo? E a parte imaginária?
2. Como representamos um número quando temos apenas a parte real?
3. E quando temos apenas a parte imaginária?
4. Como faríamos para encontrar a distância do centro até um ponto no plano dos números reais? Podemos utilizar o mesmo procedimento para os números complexos?
Em seguida, explique aos alunos como representamos o afixo (ponto) de um número complexo, como calculamos o módulo (distancia entre o centro do plano e o afixo) e o argumento (ângulo) de um número complexo e como o representamos na forma trigonométrica.
Os seguintes endereços eletrônicos podem auxiliar o professor com teoria sobre números complexos: http://www.educ.fc.ul.pt/docentes/opombo/seminario/euler/numeroscomplexos.htm e http://www.desenredo.com.br/Matematica/NumerosComplexos4.htm.
Proponha aos alunos que determinem o módulo e o argumento principal, coloque na forma trigonométrica e dê a representação gráfica dos seguintes números complexos:
4; 1 + i √3; 3i, – 5; – 2i; – 5 – 5i; 2 – 2i;
 

Laboratório de Informática:

Leve os alunos ao laboratório de informática e peça a eles que abram o recurso “Complex number”, disponível no endereço eletrônico:
http://objetoseducacionais2.mec.gov.br/handle/mec/9080.
 

O “Complex number”, mostra os valores da parte real “Re(z)” e da imaginaria “Im(z)”, calcula o módulo “Abs(z)” e o argumento “Arg(z)” do número complexo. O plano mostra a posição das coordenadas que compõem o número complexo, mostra o módulo do número através da linha verde e o seu argumento através da parte acinzentada do plano.
Com este recurso, o professor pode analisar com seus alunos o plano cartesiano para números complexos. Peça a eles que confiram os cálculos feitos na atividade em sala de aula através do recurso e, depois, proponha outra atividade. Peça a eles que montem alguns números complexos a partir da manipulação do recurso, que anotem e troquem com seus colegas para que estes encontrem os números no recurso.
Em seguida, monte com seus alunos um jogo como o de batalha naval, mas para números complexos. Você pode montar um tabuleiro a partir do papel quadriculado ou então reproduzir o tabuleiro conforme o modelo abaixo:

Regras:
1. Cada jogador deve ter um tabuleiro.
2. Em seu tabuleiro, sem que o seu oponente veja, o jogador posiciona sua esquadra composta por:
• 1 porta-aviões (4 marcas X em posições contínuas numa reta horizontal ou vertical);
• 2 submarinos (3 marcas O em posições contínuas numa reta horizontal ou vertical);
• 3 destroyers (2 marcas r em posições contínuas numa reta horizontal ou vertical);
• 4 fragatas (1 marca #);
3. A seguir alternadamente, cada jogador tem direito a "dar um tiro" falando uma posição de um número complexo com sua parte real e imaginária. Por exemplo: 3 – i;
4. Se o tiro atingir algum dos navios do adversário este diz "acertou" e especifica o tipo de navio e o jogador tem direito a novo tiro até errar. No caso do tiro não acertar nenhum navio o adversário diz "Água" e é sua vez de jogar.
5. O jogo termina quando uma das frotas for totalmente atingida e o vencedor é o jogador que conseguir afundar todos os navios de seu adversário.

Validando o conceito:

Após o jogo e ainda no laboratório de informática, peça aos alunos que façam uma pesquisa sobre aplicações de números complexos e que redijam um texto sobre as aplicações pelas quais mais se interessaram. Ao final, peça a eles que entreguem o texto a você.
Para observar se os alunos aprenderam o professor pode propor uma atividade com resolução de problemas, como os que seguem:
1. Um prefeito mandou construir uma praça de forma triangular em um bairro da cidade que administra. Sabemos que essa praça estará na posição associada aos números complexos 2, -1 + i √3 e -1 - i √3. Represente esse praça no plano dos números complexos.

Resposta: Basta representar os números complexos no plano cartesiano de Argand-Gauss e unir esses pontos formando um triângulo.

2. Em um terreno circular deve ser construído um campo de futebol que esteja no centro do terreno e que intercepte as bordas apenas nos pontos 3, 3i, -3, -3i. Qual será a forma do campo de futebol?

Resposta: Será da forma de um losango.

3. Um triangulo eqüilátero, inscrito em uma circunferência de centro na origem, tem como um de seus vértices o ponto do plano associado ao número complexo √3 + i.
a) Que números complexos estão associados aos outros dois vértices do mesmo triangulo? Faça o desenho desse triângulo.
b) Qual a medida do lado desse triangulo?

Resposta: (a) Como temos apenas a medida de um dos vértices do triangulo, devemos encontrar seu módulo e, por conseqüência, o raio da circunferência circunscrita (que será 2). Encontrando as bissetrizes dos ângulos do triângulo eqüilátero, dividimos a circunferência em três ângulos iguais, com 120º cada ângulo. Os outros dois vértices do triângulo eqüilátero inscrito na circunferência serão encontrados a partir do módulo de √3 – i e do ângulo de 120º, conforme mostra a ilustração. Esses vértices serão √3 – i e 2i.

(b) Observando os pontos (√3, -1) e (- √3, -1) e, levando em consideração que no triângulo eqüilátero a bissetriz de um ângulo divide o lado oposto em dois segmentos iguais, teremos cada um desses segmentos com a medida √3. E, portanto, o lado do triângulo eqüilátero será 2√3.

4. Um ciclista contorna uma pista circular que contem o ponto 3 + 3i. Em certo momento ele pára, completando ¾ de uma volta na pista.
a) Represente geometricamente no plano de Argand-Gauss o trajeto do ciclista.
b) Em que ponto do plano ele parou, supondo que ele saiu do ponto 3?
c) A que distância ele se encontra do centro da pista circular?
d) Escreva na forma trigonométrica o ponto de parada do ciclista.

Resposta: (a) a representação do trajeto do ciclista pode ser feita da seguinte forma:

(b) Saindo do ponto 3√2 e pedalando ¾ da volta completa, o ciclista parou no ponto -3√2i.
(c) Para calcular a distância do ciclista até o centro da pista é necessário encontrar o módulo do número complexo z = 3 + 3i, ou simplesmente observar que a medida do inicio do trajeto já fornece o raio da circunferência e, portanto, a distância procurada.
(d) Sabendo que a módulo de -3√2i = 3√2 e que cos 0/3√2 = 0 e sen (-3√2)/3√2 = - 1, então θ = 3π/2. Logo, z = 3√2 (cos 3π/2 + i sen 3π/2).
 

5. (UFRRJ-2000) Em um jogo de sinuca, uma mesa está localizada com centro na origem do plano complexo, conforme mostra a figura abaixo. Após uma tacada do centro 0, a bola preta segue na direção de Z = 1 + i, bate em A, indo em seguida até B e parando, conforme demonstra a figura abaixo. Encontre o ponto Z1 = a + bi, onde a bola branca teria parado se a tacada tivesse sido dada, com a mesma intensidade, na direção e sentido do conjugado de Z.

Resposta: Z1 = 1-3i
Para encontrar o resultado precisa-se calcular:
módulo de Z = √2; cos θ = √2/2; sen θ = √2/2. Então θ = π/4.

Para encontrar o ponto do plano dos complexos em que a bola branca iria parar, basta calcular as distâncias, seguindo o seguinte raciocínio:

OP1 = AP1 = 2                                 OP1 = A’P1 = 2                 B’ = 1 – 3i
AP2 = BP2 = 1                     A’P3 = B’P3 = 1

Dicas e sugestões:

O professor encontra exercícios resolvidos no endereço eletrônico: http://www.somatematica.com.br/emedio2.php.
 

Régua e compasso para resolver os problemas propostos.

Durante as atividades o professor pode observar se o aluno consegue representar graficamente, no plano cartesiano, um número complexo e identificar as suas partes real e imaginária, seu conjugado e seu módulo. Na atividade proposta através da pesquisa, pode-se observar se além de saber trabalhar com números complexos no plano de Argand-Gauss, os alunos também percebem a utilidade desse conceito em situações reais.