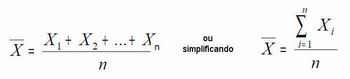Portal do Governo Brasileiro
Início do Conteúdo
VISUALIZAR CLASE
 
Medidas de Tendência Central: média, mediana e moda

 

29/06/2010

Autor y Coautor(es)
Eguimara Selma Branco
imagem do usuário

CURITIBA - PR SECRETARIA ESTADUAL DE EDUCAÇÃO

Eziquiel Menta, Gilian Cristina Barros

Estructura Curricular
Modalidad / Nivel de Enseñanza Disciplina Tema
Ensino Médio Matemática Números e operações
Ensino Médio Matemática Análise de dados e probabilidade
Educação de Jovens e Adultos - 2º ciclo Matemática Estatística, probabilidade e combinatória
Datos de la Clase
O que o aluno poderá aprender com esta aula

- Representar e analisar dados em tabelas e gráficos.

- Interpretar e resolver situações-problema que envolvam média aritmética, moda e mediana.

Duração das atividades
2 aulas - 50 minutos
Conhecimentos prévios trabalhados pelo professor com o aluno

Conhecimentos de matemática básica e interpretação de tabelas.

Estratégias e recursos da aula

Professor chame um número ímpar de alunos em pé até a frente da sala de aula e organize-os de forma crescente de altura.   

Pergunte ao restante da sala, qual a altura mediana desse grupo de alunos? Provavelmente eles irão responder que o aluno que se encontra no meio representa a "altura mediana".   

Agora professor, repita a atividade chamando um grupo par de alunos. Novamente pergunte ao restante da sala, qual a altura mediana desse grupo de alunos. Conduza o questionamento para que os alunos percebam que dessa vez, a altura mediana encontrar-se-á entre os dois estudantes que estão no meio.   

Convide novamente um grupo de alunos até a frente da sala professor, mas observe desta vez que alguns alunos tenham a mesma altura.

Converse com os alunos para que percebam que nesses casos, quando temos um mesmo valor (de altura), para mais do que um aluno, este valor designa-se por moda. No caso da moda, destaque que é possível que tenhamos mais de uma moda em uma amostra.

Chamamos de amostra, nosso grupo de análise, no caso os alunos que estão na frente da sala.   

E se nesse grupo precisarmos definir a altura média dos alunos? Como deveremos proceder? Instigue os alunos e fazerem conjecturas.

Para encontrar a média, será necessário saber as alturas de todos os alunos. De posse desses valores, devem somá-lo e então dividir pelo número de estudantes da amostra (que estão em pé a frente da sala).   

Atividade 1

Após essa vivência professor, solicite aos alunos que elaborem (com suas próprias palavras) uma definição para mediana, moda e média em seus cadernos.

Aula expositiva  

A partir das definições dos alunos, o professor deve conduzir a aula apresentando os conceitos e, na sequência propondo situações problemas (conforme segue) para verificar suas aprendizagens em relação ao tema de estudo.   

As medidas de tendência central (ou de posição) servem para destacar as características de cada distribuição, isoladamente ou em confronto com outras. São elas: média aritmética, mediana e moda.  

No caso, a média aritmética é a medida de tendência central mais utilizada, além de ser fácil de calcular, tem uma interpretação familiar e propriedades estatísticas que a tornam muito útil nas comparações entre populações e outras situações que envolvem inferências. Se os dados são de uma amostra, a média é representada pela letra x , se os dados são de uma população, a média é representada pela letra grega μ . Para uma amostra com n observações, a fórmula para a média da amostra é:

Atividade 2

Problema 1

 A tabela abaixo apresenta o consumo mensal de água de uma família durante 6 meses.

meses

consumo (m3)

janeiro

12

fevereiro

13,8

março

12,5

abril

13

maio

11,6

junho

10,3

Obs. Problema adaptado questão SAEB 2001

Pergunta-se, qual a média do consumo dessa família?   

Resolução           

         12 + 13,8 + 12,5 + 13 + 11,6 + 10,3
X = ------------------------------------------------
                                  6

X =  12, 2 m3    

Problema 2

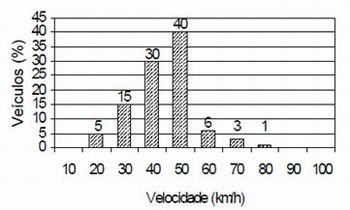
Imaginem uma cidade, onde um sistema de radar é programado para registrar automaticamente a velocidade de todos os veículos trafegando por uma avenida, onde passam em média 300 veículos por hora, sendo 55 km/h a máxima velocidade permitida. Um levantamento estatístico dos registros do radar permitiu a elaboração da distribuição percentual de veículos de acordo com sua velocidade aproximada, conforme apresenta o gráfico a seguir:

Pergunta-se, qual a velocidade média dos veículos que trafegam nessa avenida?

Obs. Problema adaptado Questão ENEM 1999

Resolução    

Nesse caso, podemos usar Vm para Velocidade Média ao invés de X. Porém, não basta somar as velocidades ou o número de veículos.

Professor, para resolver esse problema, é preciso provocar os alunos. Eles precisam perceber que quando há uma média aritmética simples todos os valores possuem um mesmo peso, situação diferente na média ponderada, que para cada valor deve-se levar em conta o valor do seu peso. Aqui no caso número de veículos x velocidade.

           20 x 5 + 30 x 15 + 40 x 30 + 50 x 40 + 60 x 6 + 70 x 3 + 80 x 1
Vm = ----------------------------------------------------------------------------
                                                            100
Vm = 44 km/h

-----

Retomando o conteúdo de medidas de tendência central, a mediana (md) é o valor, em uma série ordenada de dados, que divide a série em dois subgrupos de igual tamanho, ou seja, é um valor tal que tenha igual quantidade de valores menores e maiores do que ele. Ao contrário da média, a mediana não leva em conta todos os valores no seu cálculo, e não é afetada por valores extremos. Com os dados dispostos em ordem crescente a mediana será:

a. O valor do meio, para um número ímpar de observações.

b. A média dos dois valores centrais, para um número par de observações.  

Atividade 3   

Determine a mediana dos pesos de 7 estudantes, sendo:

58, 84, 91, 72, 68, 87, 78.   

Resolução       

Dispondo os pesos em ordem crescente, temos:   

58 68 72 78 84 87 91   

Onde a mediana será o número 78.

-----

E por fim, no conteúdo de medidas de tendência central a moda (mo) é o valor de dados que ocorre com maior freqüência, é uma importante medida de posição para os dados qualitativos. Quando dois valores ocorrem com a mesma maior freqüência, cada um é uma moda, e o conjunto de dados é bimodal. Quando mais de dois valores ocorrem com a mesma maior freqüência, cada um é uma moda, e o conjunto de dados é multimodal (ou polimodal). Quando nenhum valor se repete, dizemos que a amostra é amodal.  

Atividade 4

Qual a moda na seguinte amostra   2, 2, 3, 3, 5, 8, 8, 8, 12, 14

Resolução   

A amostra será o número 8

Atividade 5   

Em uma residência, os gastos de eletricidade são dispostos de acordo com a tabela abaixo:

Meses

jan

fev

mar

abr

mai

jun

Custo

(em €)   

35

21        

32       

 24       

33       

35     

Pede-se:

 a) média
 b) mediana
 c) moda

Resolução  

a) média

35 + 21 + 32 + 24  +  33 + 35  -->  180/6 = 30 €

b) mediana

Dispondo em ordem crescente temos

21 24 32 33 35 35 onde a mediana será 32 + 33 = 65/2 = 32,5 €

c) moda

O valor que ocorre com frequência é o 35 €

Para finalizar essa aula, o professor pode levar os alunos no laboratório de informática para que acessem o recurso Probabilidade: a matemática ao acaso (disponível em: http://objetoseducacionais2.mec.gov.br/handle/mec/1643), que desenvolve os conceitos de probabilidades, seleção de amostras e as características de uma pesquisa confiável. Esse recurso aborda ainda, conceitos de probabilidades simples e condicional; elementos de amostragem e estimativas; medidas de posição: média, mediana e moda; medidas de dispersão. 

Probabilidade: a matemática ao acaso 

PATRAO, M; LUCAS,S. Estatística – outra visão. Disponível em: http://www.educ.fc.ul.pt/icm/icm99/icm46/capa.html, acesso em 01 de junho de 2010.    

AGUIAR, R.G. Medidas de tendência central. Disponível em: http://www.engenhariaambiental.unir.br/admin/prof/arq/3.pdf, acesso em 01 de junho de 2010. 

Recursos Educacionais
Nome Tipo
Probabilidade: a matemática ao acaso Animação/simulação
Probabilidade: a matemática ao acaso Animação/simulação
Recursos Complementares

Alea - Acção Local Estatística Aplicada. Disponível em: http://alea-estp.ine.pt/, acesso em 01 de junho de 2010.  

Estatística Descritiva. Disponível em: http://www.educ.fc.ul.pt/icm/icm2003/icm24/index.html, acesso em 01 de junho de 2010. 

Média, Moda e Mediana. Disponível em: http://www.youtube.com/watch?v=SyWbYOtAIYc, acesso em 06 de junho de 2010. 

Avaliação

A avaliação deverá ser diagnóstica, processual e continua, ou seja, realizada ao longo de todas as aulas.

Critérios a serem observados:

  1. Participação na atividade inicial, discutiu a questão? colaborou com os colegas? contribuiu?
  2. Desenvolvimento e realização das atividades? Participou? Raciocínio adequado?
  3. O aluno foi argumentativo? Sua produção foi pertinente?
  4. Participação no desenvolvimento do contexto geral da aula.

Opinión de quien visitó

Quatro estrelas 22 calificaciones

  • Cinco estrelas 15/22 - 68,18%
  • Quatro estrelas 6/22 - 27,27%
  • Três estrelas 1/22 - 4,55%
  • Duas estrelas 0/22 - 0%
  • Uma estrela 0/22 - 0%

Denuncia opiniones o materiales indebidos!

Opiniones

Sem classificação.
INFORMAR ERRORES
¿Encontraste algún error? Descríbelo aquí y colabora para que las informaciones del Portal estén siempre correctas.
CONTACTO
Deja tu mensaje al Portal. Dudas, críticas y sugerencias siempre son bienvenidas.