06/07/2010
Cláudio Carlos Dias, João Carlos Vieira Sampaio, Marlusa Benedetti da Rosa
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Geometria |
| Ensino Médio | Matemática | Números e operações |
O que o aluno poderá aprender com esta aula
Esta aula se insere em um bloco de três aulas que denominamos “Ladrilhamentos do plano: geometria e arte de mãos dadas”, pertinentes ao primeiro módulo do Matem@tica na Pr@tica, um curso de especialização em matemática inserido no Plano de Ações Articuladas do MEC. Este bloco de aulas pretende organizar um ambiente provocador de aprendizagem e explorar as potencialidades pedagógicas das construções geométricas. Nosso objetivo geral é abordar conteúdos como polígonos regulares, seus ângulos internos, entre outros, de maneira que os alunos compreendam a importância do que estão estudando. Propomos uma atividade experimental como desencadeadora do processo, pois acreditamos que esse tipo de atividade possibilita momentos de reflexão e cooperação entre os alunos, além do aspecto lúdico e motivador que um experimento permite desenvolver. Caso você tenha interesse em conhecer o bloco como um todo, as aulas estão organizadas na seguinte sequência: 1- “A arte no plano: confeccionando ladrilhos e construindo ladrilhamentos”; 2- “Ladrilhamento do plano: ângulos internos e ladrilhos de três em três”; 3- “Ladrilhando o plano: mais de três ladrilhos por vez”.
Nesta aula, o aluno poderá aprender sobre polígonos regulares, seus ângulos internos e a relação que existe entre eles em um ladrilhamento, a partir de observações feitas em uma experiência prática de construção de ladrilhamentos. Esses conceitos serão abordados de forma integrada para que o aluno perceba como cada um deles é uma ferramenta importante e necessária para o entendimento de questões geométricas.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Polígonos convexos, polígonos regulares, medidas dos ângulos internos de um polígono regular, noções de dependência de variáveis, propriedades de desigualdades de números reais.
Recomendamos que esta aula seja realizada após a aula “A arte no plano: confeccionando ladrilhos e construindo ladrilhamentos”, onde a experiência prática já foi realizada e a construção dos ladrilhamentos começou a ser desenvolvida e analisada através de três regras, denominadas regras de bom comportamento.
Estratégias e recursos da aula
Estratégias
- Aula experimental com sugestão de roteiro no final.
- Aula expositiva para a problematização da atividade prática e o desenvolvimento dos conceitos matemáticos.
Recursos
- Roteiro para a realização do experimento “Mãos na massa: construindo ladrilhos e descobrindo ladrilhamentos” preenchido na Aula 1: "A arte no plano: confeccionando ladrilhos e construindo ladrilhamentos".
- Estudo Dirigido sobre o experimento realizado na Aula 1: "A arte no plano: confeccionando ladrilhos e construindo ladrilhamentos".
- Roteiro para nortear o desenvolvimento geométrico e algébrico dos ladrilhamentos analisados, “Ladrilhamentos (k,ℓ,m): analisando ladrilhos de três em três”.
Atividades
Esta aula está dividida em três momentos.
No primeiro momento, o professor deve retomar o que foi realizado na aula anterior ("A arte no plano: confeccionando ladrilhos e construindo ladrilhamentos") para situar os alunos e dar continuidade ao processo de construção dos ladrilhamentos iniciado.
No segundo momento, o professor irá estimular os alunos a relacionarem os ladrilhamentos construídos com elementos básicos da geometria.
Por fim, no terceiro momento da aula, o professor irá analisar essa relação, junto com a turma, utilizando argumentos geométricos e algébricos como uma ferramenta matemática para definir quais ladrilhamentos, com três ladrilhos concorrendo em cada vértice, podem ladrilhar um plano.
Lembramos que a ideia de realizar as aulas "A arte no plano: confeccionando ladrilhos e construindo ladrilhamentos" e "Ladrilhamentos do plano: ângulos internos e ladrilhos de três em três" é uma sugestão. No entanto, se você ainda não tiver realizado a aula "A arte no plano: confeccionando ladrilhos e construindo ladrilhamentos" com sua turma, o roteiro do experimento, bem como o estudo associado a ele, podem ser encontrados no Portal dos Professores. Se esse for o seu caso, esteja atento, pois o tempo estimado para esta aula "Ladrilhamento do plano: ângulos internos e ladrilhos de três em três" terá que ser maior.
Primeiro momento - Relembrando o experimento da aula “A arte no plano: confeccionando ladrilhos e construindo ladrilhamentos”
A primeira atividade desta aula consiste em uma recapitulação da atividade experimental realizada na aula "A arte no plano: confeccionando ladrilhos e construindo ladrilhamentos", bem como das discussões realizadas a partir da construção dos ladrilhamentos. Para essa recapitulação, sugerimos que o professor peça aos alunos que peguem o roteiro que receberam na aula "A arte no plano: confeccionando ladrilhos e construindo ladrilhamentos" e que relembrem todas as etapas realizadas no experimento. Depois, o professor deve solicitar que os alunos observem as perguntas do roteiro que responderam e corrigiram.
Quando os alunos tiverem feito isso, o professor deve retomar as questões lembrando o que foi discutido. É importante que o professor comente pausadamente as questões da etapa 3 do roteiro discutido na primeira aula desse bloco, relembrando e dando ênfase às três regras de bom comportamento estudadas e analisadas nos ladrilhamentos construídos.
Segundo momento – Relacionando os ladrilhamentos com elementos básicos da geometria
O professor pode começar esse momento da aula fazendo o aluno relembrar que somente alguns ladrilhamentos atenderam as regras de bom comportamento e pode questioná-los da seguinte forma: “Qual é a relação das regras de bom comportamento com os ângulos internos dos ladrilhos construídos?”
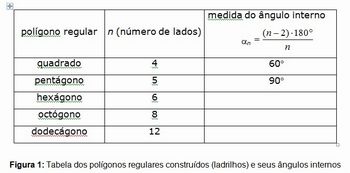
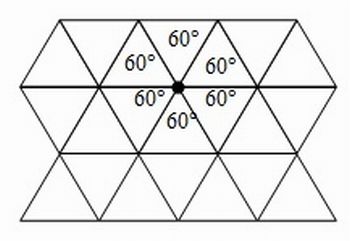
Permita que os alunos reflitam sobre a questão e levantem hipóteses. Nesse momento, é importante escutá-los − o professor pode inclusive anotar as hipóteses que surgirem na lousa. Para facilitar a percepção dos seus alunos, você pode fazer uma tabela com os polígonos que foram construídos nas etapas 1 e 2 do roteiro da aula anterior (N.P: inserir link) e pedir para que sua classe calcule qual é o valor do ângulo interno correspondente a cada ladrilho. Observe a Figura 1:
É importante que o professor oriente os alunos para que eles percebam que, a partir desse momento, estão dando um passo importante na aula, pois irão descobrir quais são os pressupostos matemáticos que estão por trás dos ladrilhamentos possíveis, ou seja, daqueles que atendem às “regras de bom comportamento”.
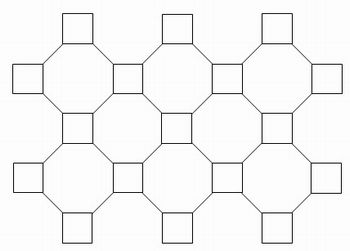
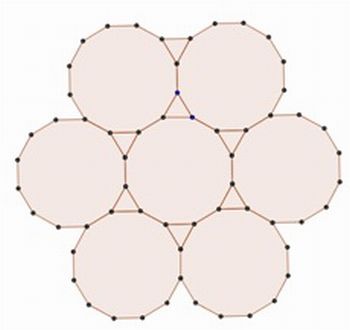
Inicialmente, o professor deve escolher um dos ladrilhamentos construídos na aula anterior, como no exemplo da Figura 2. Nesta figura está representado um ladrilhamento semirregular formado por dois octógonos e um quadrado ao redor de cada vértice.
Figura 2: Ladrilhamento formado por dois tipos de ladrilhos: ladrilhos com quatro lados e com oito lados.
Primeiramente, escolha um ladrilhamento possível e mostre por que as regras de bom comportamento foram atendidas. Depois, escolha um ladrilhamento em que pelo menos uma das regras não é atendida.
Para que um ladrilhamento possa ser considerado “bem-comportado”, a primeira regra diz que os polígonos que o constituem precisam ser regulares, ou seja, é necessário que eles possuam todos os lados e ângulos internos iguais. Enfatize que essa regra nunca será quebrada, pois os moldes feitos na etapa 1 da aula anterior eram todos de polígonos regulares. Além disso, a segunda regra define que a interseção entre os polígonos deve ser sempre um lado ou um vértice. Garantidas essas condições, a soma dos ângulos internos adjacentes a cada vértice será igual a 360º, para que não existam sobreposição nem espaços vazios entre eles. Por fim, para que a terceira regra seja atendida, a distribuição de ladrilhos ao redor de cada um dos vértices do ladrilhamento deverá ser sempre a mesma. Mostre para os alunos que, às vezes, pode acontecer de a primeira e a segunda regra serem atendidas, mas a terceira não.
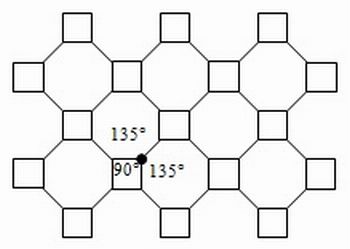
No exemplo da Figura 2, temos dois octógonos regulares e um quadrado em torno de cada vértice. A soma dos ângulos internos dos ladrilhos que se posicionam em torno de cada vértice é precisamente 360°.
135º + 135º + 90º = 360º
Logo, ele atende as três regras de bom comportamento, pois é formado por polígonos regulares, não há vazios nem sobreposições entre os ladrilhos (ou seja, a soma dos ângulos internos adjacentes a cada vértice é igual a 360º), e a distribuição de ladrilhos ao redor de cada vértice do ladrilhamento é sempre a mesma.
Terceiro Momento – Analisando ladrilhamentos formados por três polígonos ao redor de cada vértice
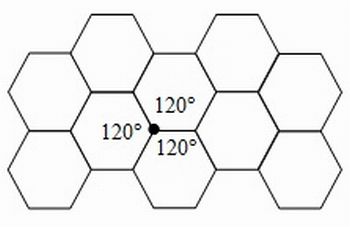
Para restringir o estudo dos diversos tipos de ladrilhamentos bem-comportados, comece mostrando para seus alunos que um vértice admite no máximo seis ângulos de 60º adjacentes a ele, ou seja, seis triângulos equiláteros, e no mínimo 3 polígonos regulares, como sugerido nos exemplos da Figura 3 a seguir:
Figura 3: Na figura da esquerda, note que ao redor de cada vértice temos 6 × 60° = 360°; na figura central, temos que 3 × 120° = 360°; no figura da direita, a soma dos ângulos internos adjacentes ao vértice é igual a 2 x 135° + 90° = 360°. Assim, podemos concluir que teremos no mínimo três polígonos regulares, uma vez que, com dois polígonos regulares, não é possível constituir um ladrilhamento. E ainda que, quando consideramos seis polígonos regulares ao redor de um mesmo vértice, se pelo menos um deles não é um triangulo equilátero, a soma doa ângulos internos seria maior do que 360°.
Diante disso, conduza sua turma a descobrir geometricamente os ladrilhamentos do plano constituídos de três polígonos adjacentes a cada vértice.
A estratégia é descobrir quais são os polígonos que constituem esse padrão de ladrilhamento. Opte por começar pelo caso mais simples, ou seja, aquele onde um dos ladrilhos é um triângulo, mais precisamente um ladrilhamento de padrão (3,ℓ,m), isto é, um ladrilhamento que tem um triângulo, um ℓ-ágono regular (polígono regular de ℓ lados) e um m-ágono regular (polígono regular de m lados).
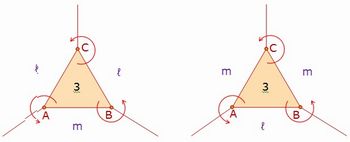
Desenhe o triângulo equilátero de vértices A, B, C e a disposição dos outros ladrilhos em torno dele, conforme ilustrado na Figura 4:
Figura 4: Seguindo a orientação dada pelas setas e comparando, observamos que os tipos dos vértices A e B são equivalentes.
Na Figura 4, ao realizarmos um percurso circular em torno do vértice A, no sentido anti-horário, identificamos esse vértice como sendo do tipo (3,ℓ,m). Se o percurso circular for feito no sentido horário, então vemos que o mesmo vértice tem o tipo (3,m,ℓ). Por esse motivo, em um contexto geral, consideramos como equivalentes vértices dos tipos (3,ℓ,m) e (3,m,ℓ).
Agora faça com que os alunos percebam que o vértice A é do tipo (3,m,ℓ), o vértice B é do tipo (3,ℓ,m) e o vértice C é do tipo (3,ℓ,ℓ) ou (3,m,m), dependendo de qual é o polígono adjacente ao lado AC do triângulo. E, como todos os vértices têm que ser de um mesmo tipo, para que a terceira regra de bom comportamento seja atendida, então ℓ = m. Ou seja, o ladrilhamento é de padrão (3,m,m). Assim, vemos que os padrões (3,ℓ,ℓ) e (3,m,m) passam a ser um só.
Relembre que, para que o ladrilhamento seja bem-comportado, a soma das medidas dos ângulos dos polígonos que concorrem em um mesmo vértice tem que ser igual à medida do ângulo de uma volta completa, isto é, 360º. Relembre também que, se um polígono regular tem n lados, então cada ângulo interno an é dado pela igualdade:
an = 180º (n-2) / n
Utilizando a expressão acima e voltando ao ladrilhamento de padrão (3,m,m), deveremos ter: a3+am+am=360o , ou seja, 60o+2 am=360o e, portanto, am=150o
Usando a fórmula anterior, conclua que m = 12. Por isso, o ladrilhamento é de padrão (3,12,12) – triângulo-dodecágono-dodecágono – e se encontra ilustrado na Figura 5.
Figura 5: Ladrilhamento de padrão (3,12,12)
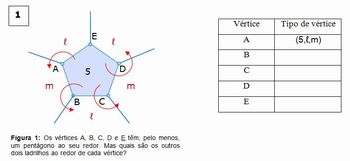
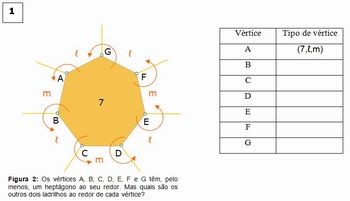
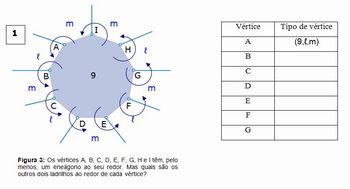
Convide os alunos a imitarem o método anterior para concluir que não existem ladrilhamentos de padrões (5,ℓ,m), (7, ℓ,m) e (9,ℓ,m).
Se o ladrilhamento tem padrão (k,ℓ,m), com pelo menos um dos valores k,ℓ,m sendo ímpar, então podemos assumir que o valor ímpar seja o valor de k. Além disso, em todos os casos em que k = 3, 5, 7 ou 9 podemos deduzir que necessariamente ℓ = m. Usando a equação da soma dos ângulos internos adjacentes a cada vértice,ak+am+am=360o , podemos concluir que para todo os casos em que k é ímpar, a única solução possível é aquela em que k = 3 e m = 12. Assim, o único ladrilhamento bem-comportado de padrão (k,ℓ,m), com k ímpar, é (3,12,12).
Você pode dividir a turma em grupos e orientar esse estudo seguindo a etapa 1 do roteiro “Ladrilhamentos (k,ℓ,m): analisando ladrilhos de três em três”, disponível no final. Durante a realização deste tipo de atividade, é interessante que cada aluno responda seu próprio material, pois ele servirá mais tarde de fonte de consulta. Além disso, o preenchimento do roteiro mantém a atenção de todos na atividade.
Não se esqueça de orientar os alunos para que leiam as instruções de cada etapa e que registrem os dados no roteiro. Reafirme a importância do debate entre os membros do grupo sobre as respostas de cada questão. Se você achar que seus alunos não possuem autonomia para iniciarem sozinhos o desenvolvimento matemático, explique o procedimento antes que eles comecem a fazer o trabalho.
Tendo estudado ladrilhamentos de padrão (k,ℓ,m) em que pelo menos um dos ladrilhos tenha um número ímpar de lados, para finalizar esta aula, resta, portanto, estudar os ladrilhamentos de padrões (k,ℓ,m) que façam uso somente de polígonos regulares, com números pares de lados. Mais uma vez, comece pelo estudo de ladrilhamentos que admitem o polígono regular que possui o menor número par de lados: o quadrado.
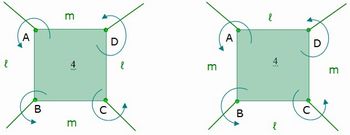
Para manter um raciocínio análogo ao anterior, desenhe o quadrado de vértices A, B, C e D e a disposição dos outros ladrilhos em torno dele, conforme ilustrado na Figura 6:
Figura 6: Seguindo a orientação dada pelas setas, os vértices A, B, C e D possuem tipos equivalentes em ambas as figuras.
Novamente, faça com que os alunos vejam que, seguindo a orientação das setas, o vértice A é do tipo (4,m,ℓ), o vértice B é do tipo (4,ℓ,m), o vértice C é do tipo (4,m,ℓ) e o vértice D é do tipo (4,ℓ,m). Note que nesse caso não é preciso que tenhamos ℓ = m.
Relembre que a soma das medidas dos ângulos dos polígonos adjacentes a um mesmo vértice tem que ser igual a 360º para atender a segunda regra de bom comportamento. Considere que, nesse ladrilhamento, essa soma deverá ser feita da seguinte forma:
a4+aℓ+am=360o
Como a4 = 90°, ficamos com a equação aℓ + am = 270° .
Para descobrir quais são os polígonos que compõem o vértice desse ladrilhamento, use a equação que define a medida dos ângulos internos de um polígono regular qualquer, aℓ ou am :
aℓ = 180º (ℓ-2) / ℓ = 180º ( 1 -2/ℓ )
am = 180º (m-2) / m = 180º ( 1 -2/m )
Ora, se a soma dos ângulos internos do ℓ-ágono e do m-ágono concorrentes em um vértice deve ser 270º, então mostre para sua turma que:
180º ( 1 -2/ℓ )+180º ( 1 -2/m )=270º
ou, equivalentemente,
2/ℓ + 2/m = 1/2
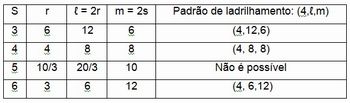
Como ℓ e m são inteiros pares, ambos são múltiplos de 2. Assim ℓ = 2r e m = 2s, para certos inteiros positivos r e s. Nossa última equação envolvendo ℓ e m transforma-se então na equação
1/r + 1/s = 1/2
Isolando a variável r chegaremos a
r = 2s / (s-2) = ( 2(s-2) + 2) / (s-2) = 2 + 2 / (s-2)
É necessário ressaltar que, para que o denonimador permaneça sempre positivo, devemos ter s>2. Como r é um número inteiro, então s-2 deverá ser um divisor de 4, logo s atinge seu valor máximo quando s-2=4 , ou seja, s=6. Assim, concluímos que 2<s<7.
Pronto! Agora ficou fácil definir possíveis valores de ℓ e m. Usando a igualdade r = 2s / (s-2), podemos construir a seguinte tabela:
Por fim, convide os alunos a imitarem o método algébrico explicado acima, para pesquisar os ladrilhamentos de padrões (6,ℓ,m) e (8,ℓ,m). Utilize a etapa 2 do roteiro “Ladrilhamentos (k,ℓ,m): analisando ladrilhos de três em três” para conduzir esse estudo.
Faça os alunos observarem que, se um ladrilhamento de padrão (k,ℓ,m), com k,ℓ,m todos pares, não contém nenhum quadrado, então ele é o ladrilhamento regular (6,6,6). Além disso, é impossível a existência de um ladrilhamento de padrão (k,ℓ,m) com k,ℓ,m todos pares que não contenha quadrados nem hexágonos.
Roteiro " Ladrilhamentos (k,ℓ,m): analisando ladrilhos de três em três "
Identifique sua instituição:
Professores envolvidos:
Disciplinas: Aluno(a):_________________________________Turma:______Grupo:______
Ladrilhamentos (k,ℓ,m) : analisando ladrilhos de três em três
Introdução:
Analisaremos geometricamente os padrões de ladrilhamentos (5,ℓ,m), (7,ℓ,m) e (9,ℓ,m) e algebricamente os padrões (6,ℓ,m) e (8, ℓ,m).
Procedimento:
Etapa 1- Padrões (5,ℓ,m), (7,ℓ,m), (9,ℓ,m) em xeque
Para desenvolver essa atividade, siga o seguinte passo a passo:
- Observe as figuras e preencha as tabelas relativas a cada uma delas.
- Descubra geometricamente quais são os polígonos ℓ e m, caso existam.
- Analise o estudo feito no item 2 e responda a pergunta que virá a seguir.
CASO (5,ℓ,m)
CASO (7,ℓ,m)
CASO (9,ℓ,m)
Etapa 2 - Padrões (6,ℓ,m) e (8,ℓ,m) em foco
Havendo um ladrilhamento de padrão (6,ℓ,m) ou (8,ℓ,m) e considerando as regras de bom comportamento, sabemos que a soma dos ângulos internos dos polígonos ao redor de cada vértice deve ser igual a 360º.
Logo, temos as seguintes expressões matemáticas:
- a6 + aℓ + am = 360°
- a8 + aℓ + am = 360°
Utilize o desenvolvimento algébrico análogo ao ensinado durante a aula para responder a questão a seguir:
Existe algum ladrilhamento bem-comportado de padrão (6,ℓ,m) ou (8,ℓ,m)? Caso exista, diga se ele é regular ou semirregular.
Recursos Complementares
[1] Software livre de desenho geométrico: www.geogebra.org.
[2] http://matematica.incubadora.fapesp.br/portal/textos/matematicaladrilhos/ladrilhamentos.pdf.
[3] Revista do professor de Matemática Nº 40 e Nº70 – ISSN 0102-4981.
Avaliação
A avaliação desta aula pode ser feita através da análise das respostas às perguntas feitas pelo professor. O professor pode avaliar o que os alunos aprenderam na aula anterior no momento de recapitular a aula "A arte no plano: confeccionando ladrilhos e construindo ladrilhamentos". Além disso, o professor pode avaliar o acompanhamento e o envolvimento dos alunos nas discussões. Pode ainda avaliar os alunos por meio das respostas, dúvidas e questões que surgirem na realização do roteiro “Ladrilhamentos (k,ℓ,m): analisando ladrilhos de três em três”.
Cinco estrelas 2 classificações
- Cinco estrelas 2/2 - 100%
- Quatro estrelas 0/2 - 0%
- Três estrelas 0/2 - 0%
- Duas estrelas 0/2 - 0%
- Uma estrela 0/2 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
DIonice ferreira da Silva, IFRN , Rio Grande do Norte - disse:
dionice_te@yahoo.com.br13/12/2014
Cinco estrelasMuito interessante, fiz para 9 ano claro que buscando trabalhar ladrilhamento . Entretanto abordei de um jeito mais fácil para que eles entendesse a classificação quanto os lados e medidas dos ângulos.
-
Yasmin Oliveira, Plinio , São Paulo - disse:
Naopossocolocardescupa@hotmail.com02/09/2014
Cinco estrelasparabéns pela pagina gostei muito e me ajudou!!!! queria que voces relatacem sobre a apostila do 7 ano de matematica para aprender mais....grata! Coloquem aqui na pagina sempre vou vir se vcs me responderam!!!!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus