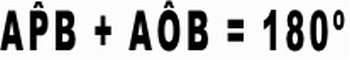Reconhecer e representar ângulo circunscrito.

Construam retas tangentes à circunferências e vice-versa com base nas suas propriedades.

Resolvam problemas gráficos aplicando as propriedades de tangência.    

Circunferência, ângulo inscrito, ângulo central e ângulo de segmento.

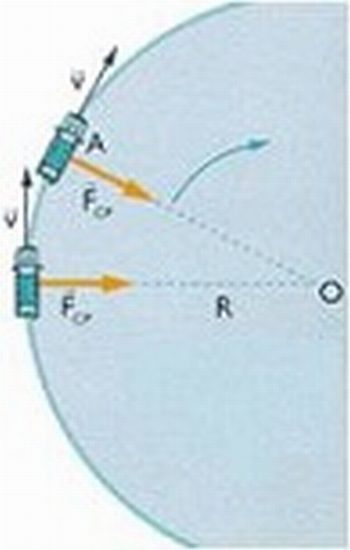
"Quem dirige um carro deve saber que nem todas as curvas podem ser feitas a uma certa velocidade. Isto porque o veículo não consegue continuar "colado" na pista e sai pela tangente."

http://ciencianotransito.blogspot.com/2009/11/centripeta-forca-presente-nas-curvas.html  

Como motivação, coloque no quadro a frase acima e discuta com os alunos o que quer dizer “sair pela tangente”.

 Desenhe no quadro uma circunferência e uma reta tangente a ela. Explore as propriedades envolvidas.

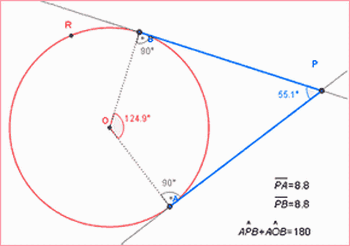
 Defina ângulo circunscrito e enuncie a  seguinte propriedade: Se os dois lados de um ângulo de vértice P são tangentes a um círculo nos pontos A e B, então: (a) a medida do ângulo P é

 igual a 180º menos a medida do arco menor determinado por A e B; (b) PA = PB.

 Se possuir um computador ligado a um projetor, explore a propriedade com o Applet: http://ava.ead.ftc.br/conteudo/circuito1/Circuito_Novo/Periodo_02/matematica/03-fundamentos_da_geometria/bloco2/tema3/applets-tema3/propo-11-100.ht   e estimule os alunos a perceberem que como a figura AOBP é um quadrilátero, a soma dos ângulos internos é 360º e como, pela propriedade da tangência, os ângulos PAO e PBO são retos, temos

ATIVIDADE 1: NO LABORATÓRIO DE INFORMÁTICA - EM DUPLAS

Peça que os alunos acessem o site http://www.dm.ufscar.br/~caetano/SiteDG/ICSilvia/RetaTangente.htm  

e observem a construção geométrica do seguinte exercício:

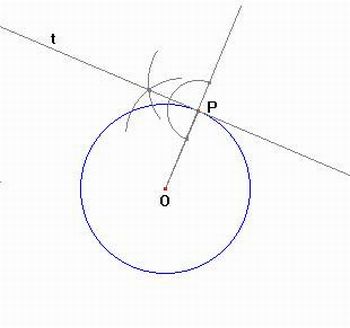
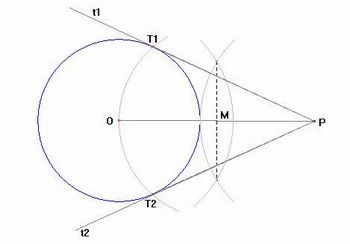
Dado um círculo de centro O e um ponto P, traçar a reta tangente à circunferência que passa por P.     

Eles devem registrar, em seus cadernos, um esboço da resolução e as etapas de construção, justificando-as pelas propriedades de tangência. É importante que ao analisarem a construção geométrica, eles percebam a relação entre ângulo inscrito e ângulo central. Para isso, eles devem solicitar sua ajuda. Seria interessante que você não dê a resposta e sim estimule-os a procurarem propriedades conhecidas.

A seguir, solicite uma pesquisa sobre outros tipos de tangência, incluindo tangência entre circunferências, e sua aplicação na construção de espirais.

ATIVIDADE 2

Em sala de aula, com o auxílio dos materiais de Desenho Geométrico (compasso e par de esquadros), os alunos devem resolver o primeiro exercício apresentado no laboratório de informática, usando os registros feitos nos cadernos. A seguir, proponha a resolução de outro exercício, que pode ser encontrado no site:

  http://pcc2100.pcc.usp.br/COL/exerciciosDG.html  

ATIVIDADE 3

A partir da pesquisa realizada pelos alunos, discuta com os alunos sobre a aplicação de tangência na construção de concordâncias e sua aplicação prática.

Arcos da Lapa,  Rio de Janeiro

 http://www.fashionbubbles.com/wp-content/uploads/2009/01/arcos_da_lapa.jpg

Catedral de Amiens, França

http://upload.wikimedia.org/wikipedia/commons/thumb/0/0e/Amiens_cathedral_031.JPG/240px-Amiens_cathedral_031.JPG 

Escada Em espiral do Vaticano

http://www.fotosphotos.com/images/arch02.jpg 

Proponha como trabalho pratico a confecção de um sino de vento. Você encontra instruções de como fazer no link abaixo:

http://viniluzzi.wordpress.com/2009/07/26/mtas-coisas/ 

Apostila de Desenho Geométrico:

http://www.scribd.com/doc/271620/apostila-de-desenho-geometrico 

Avalie a aula pelos registros feitos pelas discussões feitas com os alunos e pelos registros das atividades.