30/09/2010
Eziquiel Menta
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Geometria |
| Educação de Jovens e Adultos - 2º ciclo | Matemática | Grandezas e medidas |
| Ensino Médio | Matemática | Números e operações |
O que o aluno poderá aprender com esta aula
§ Identificar as aplicações dos fractais na matemática.
§ Aplicar as propriedades dos fractais em situações matemáticas.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Conhecimentos de geometria e matemática.
Estratégias e recursos da aula
Para começar essa aula, o professor pode passar aos alunos o vídeo Fractais na Natureza, disponível em: http://www.youtube.com/watch?v=DwsoxSN-8Xg, em 02 de agosto de 2010.
Durante a apresentação do vídeo, o professor pode fazer pausas e propor reflexões a respeito das diversas imagens e situações que o vídeo apresenta. Lembrando que os fractais estão em toda parte, podem ser brilhantes, estranhos e diferentes...
Sugestão de encaminhamentos durante o vídeo:
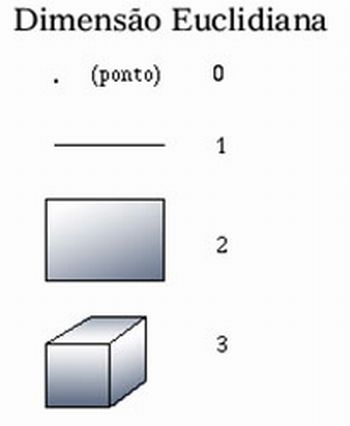
Na geometria clássica, o conceito de dimensão usado é o euclidiano, e esse conhecimento é algo muito antigo. Nesta dimensão, os objetos são relacionados ao espaço no qual estão inseridos. Assim, retas e curvas têm dimensão 1; plano, dimensão 2; espaço, dimensão 3 e, por indução, pode ampliar-se sucessivamente até n dimensões. Salienta-se que as dimensões euclidianas são números inteiros. Essa noção permeou a matemática por muitos e muitos anos. Alguns matemáticos até observavam algumas disparidades, mas nenhum deles ousou contrariar o que foi postulado por Euclides.
Fonte: http://marte.dpi.inpe.br/col/dpi.inpe.br/lise/2001/09.19.12.25/doc/0811.818.082.pdf
Até que, um matemático francês, Mandelbrot, afirmou que "Há alguma razão para a geometria não descrever o formato das nuvens, das montanhas, das árvores ou a sinuosidade dos rios? Nuvens não são esferas, montanhas não são cones, continentes não são círculos, um latido não é contínuo, e nem o raio viaja em linha reta...” (MANDELBROT,1983)
Pois percebeu que muitos fenômenos e formas encontradas na natureza não poderiam ser explicados nos moldes da matemática convencional, sendo para isso necessário uma nova teoria que desse conta dessas diferentes formas geométricas. Tanto o padrão de formação de nuvens quanto o padrão de crescimento e disposição de galhos e folhas em uma árvore podem ser recriados por meio de regras simples de construçãao geométrica, mas que ao serem executadas são capazes de gerar estruturas de complexidade admirável: os fractais.
Afinal, o que são fractais???
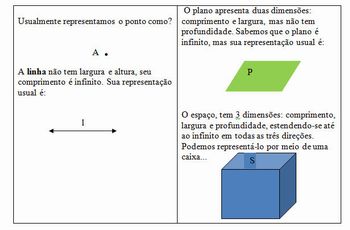
| A maioria da matemática que estudamos hoje na escola é um conhecimento muito antigo. Por exemplo, a geometria foi organizada em torno de 300 a.C. por um matemático chamado Euclides. Para ele o mundo só poderia ser representado por formas conforme mostra a imagem... |
|
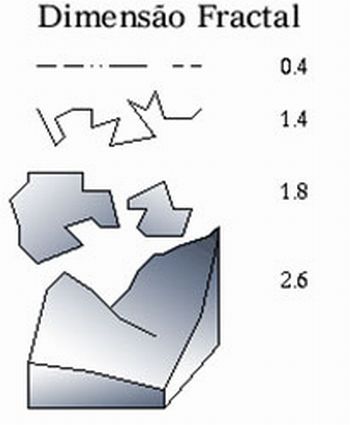
| Porém, a maioria dos objetos na natureza não é formada por linhas e/ou curvas, quadrados ou triângulos, mas por figuras geométricas bem mais complicadas. Mandelbrot, no ínicio dos anos 80, chamou de fractais (verbo frangere, que significa quebrar, fracturar, irregular), a classificação de certos objetos que não continham uma dimensão inteira, podendo ter dimensão fracionada. Embora esses “monstros matemáticos” já existissem há muito tempo, ninguém lhes havia atribuído nenhum nome. Veja como fica a representação do mundo a partir da dimensão fractal... |
Fonte: http://www.insite.com.br/fractarte/artigos/dimensionalidade.gif
Vale lembrar que uma das contribuições para a reformulação da geometria, foi o surgimento da tecnologia e dos softwares que permitiram a construção de situações imaginárias que se repetiam...
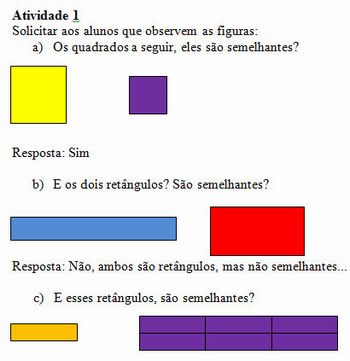
Resposta: Na geometria, dizemos que duas figuras são semelhantes se elas possuírem a mesma forma.
Observe atentamente o retângulo roxo, ele é 2 vezes mais largo que o retângulo laranja e 3 vezes mais comprido. Os lados correspondentes são proporcionais (ângulos correspondentes também são da mesma medida), portanto, dizemos que essas figuras são auto-semelhantes.
Muitas figuras são auto-semelhantes. Observe o triângulo a seguir.
Aqui, o professor pode propor que os alunos desenvolvam outras figuras semelhantes.
Continuando...
Para ser um fractal, as formas geométricas precisam apresentar determinadas características, a auto-semelhança é uma dessas características.
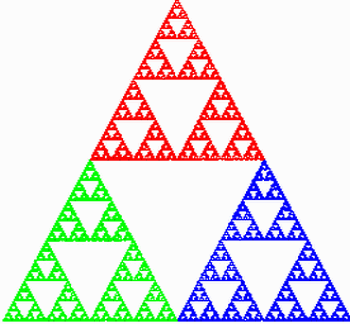
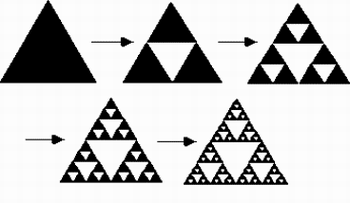
Agora observe a seguinte figura chamada Triangulo de Sierpinski:
Fonte: http://www.terra.es/personal/davinci9/leuka/triang1.gif
Seu contorno é de um triângulo equilátero. Agora olhe para dentro de todos os outros triângulos. Há um número infinito de triângulos cada vez menores no interior, correto? Cada um desses triângulos é semelhantes entre si e ao triângulo original. Esta é uma representação de auto-semelhança na geometria fractal. Auto-semelhança é uma das importantes propriedades dos objetos fractais.
Atividade 2
Professor converse com os alunos, sempre questionando... Explique que na matemática, alguns objetos matemáticos são abstratos, ou seja, são imagináveis. Esses conceitos polêmicos envolvem muita filosofia e dedução matemática. Como exemplo pode citar o ponto, na vida real, o ponto não existe em representação. Não podemos pegar um ponto, pois ele não tem dimensões, nem comprimento, nem largura, nem altura. Mas todos sabemos como é um ponto. Por que imaginamos como ele seja, já abstraimos essa ideia. Dá mesma forma, imaginamos como seja a reta e o plano.
Clique sobre a imagem a seguir para ver a orientação ampliada.
Assim como os objetos até aqui representados, também os fractais possuem seu nível de abstração. Observe:
Vamos organizar essas informações. Preencha o quadro com as respostas dos alunos.
| Figura |
Dimensão |
Cópias |
| Segmento de linha |
1 |
2 = 21 |
| Quadrado |
2 |
4 = 22 |
| Cubo |
3 |
8 = 23 |
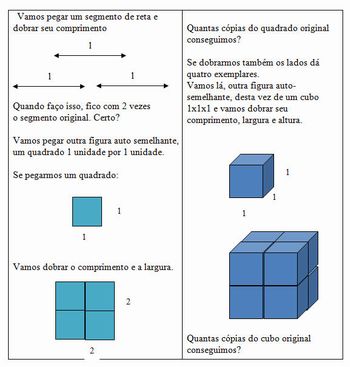
Observe que na medida em que dobramos os lados de cada figura, escrevemos as cópias com uma potência de 2.
Perceba que neste padrão, a dimensão é o expoente. Vamos então acrescentar mais uma linha a nossa tabela.
| Figura |
Dimensão |
Cópias |
| Segmento de linha |
1 |
2 = 21 |
| Quadrado |
2 |
4 = 22 |
| Cubo |
3 |
8 = 23 |
| Duplicação da Semelhança |
d |
n = 2d |
Agora, voltemos ao Triângulo de Sierpinski, quando você dobra o comprimento dos lados, tem outro Sierpinski semelhante ao primeiro, certo?
Fonte: http://www.terra.es/personal/davinci9/leuka/triang1.gif
Vamos pensar. Se atribuirmos que um triângulo de Sierpinski tem 1 unidade de medida de lado, ao dobrar o comprimento dos lados, quantas cópias do triângulo original teremos?
Lembre-se de desconsiderar os triângulos que são espaços vazios, não podemos contá-los. Dobrar os lados nos dá três cópias, para 3 = 2d, onde d = a dimensão. Mas espere, 2 = 21 e 4 = 22, assim que número poderia ser isso? Tem que estar em algum lugar entre 1 e 2, certo?
Assim, acrescentamos mais uma linha a tabela anterior...
| Figura |
Dimensão |
Cópias |
| Segmento de linha |
1 |
2 = 21 |
| Triângulo de Sierpinski |
? |
3 = 2? |
| Quadrado |
2 |
4 = 22 |
| Cubo |
3 |
8 = 23 |
| Duplicação da Semelhança |
d |
n = 2d |
Portanto, a dimensão do Triângulo de Sierpinski é entre 1 e 2. Por isso, dizemos que fractais podem ter dimensão fracionária. A dimensionalidade é outra característica dos fractais.
Atividade 3
Todos os fractais são formados por iteração. Mas, o que isso quer dizer? Fazer um fractal de uma figura geométrica conhecida (triângulo ou segmento de linha) significa fazê-lo novamente e novamente... e novamente.
Na verdade, você tem que fazê-lo infinitas vezes. Vamos tentar!!
Acompanhe os passos:
Fonte: http://www.terra.es/personal/davinci9/leuka/triang2.gif
Primeiro Passo - Desenhe um triângulo equilátero com lados de comprimento 2. Ligue os pontos médios de cada lado. Quantos triângulos equiláteros que você tem agora? Corte o triângulo no centro.
Segundo Passo - Dentro de cada triângulo eqüilátero, desenhe outros 4 triângulos, faça pelos pontos médios dos lados e corte os triângulos dos centros, como antes. Observe os três pequenos triângulos que também precisam ser cortadas em cada um dos três triângulos – teremos mais 3 buracos.
Terceiro Passo - Siga o mesmo procedimento de antes, certificando-se de seguir o padrão de corte.
Quarto Passo - Para este, você precisará mais precisão. Siga o padrão anterior para completar a quarta etapa do Triângulo de Sierpinski. Use a sua criatividade artística, pode usar cores e/ou sombra. Se sua figura está como a última da figura indicada, então você está correto!
Assim, descobrimos mais uma das características dos fractais, o fato de serem gerados por um padrão de repetição recorrente ou iterativo.
Além de se apresentarem como formas geométricas, os fractais podem também ser representados matematicamente. Porém, para ser um fractal, precisam apresentar as características conforme vimos: auto-semelhança, dimensionalidade e processo iterativo.
Visualizar as caracteristicas fractais doTriângulo de Sierpinski por meio do vídeo que mostra o zoom deste triângulo. Disponível em: http://www.youtube.com/watch?v=QsMvoui5WlQ, acesso em acesso em 02 de agosto de 2010.
Atividade 4
Para finalizar essa aula, o professor pode levar a turma ao laboratório de informática, onde poderão desenvolver alguns fractais a partir do software educacional Fractal Explorer, disponível em: http://objetoseducacionais2.mec.gov.br/handle/mec/3591, observando as propriedades estudadas na aula (no caso da escola não dispor de laboratório, o professor pode projetar aos alunos diferentes fractais elaborados a partir do software).
Sugestão Interdisciplinar
Para essa aula, convide os professores da disciplina de Ciências para trabalhar os efeitos da música fractal na saúde. Da mesma forma, os professores de Artes poderão discorrer sobre as manifestações artisticas a partir da geometria fractal.
Referências
Estimativa da dimensão fractal de nuvens em imagem de satélites meteorológicos. Disponível em: http://marte.dpi.inpe.br/col/dpi.inpe.br/lise/2001/09.19.12.25/doc/0811.818.082.pdf, acesso em 10 de setembro de 2010.
Recursos Complementares
- O Mundo dos Fractais. Disponível em: http://www.educ.fc.ul.pt/icm/icm99/icm14/index.htm, acesso em 02 de agosto de 2010.
- Exposição de Fractais. Grupo Fractarte. Disponível em: http://www.fractarte.com.br/index.php, acesso em 02 de agosto de 2010.
- Geometria Fractal: arte ou ciência. Disponível em: http://www.youtube.com/watch?v=q-61Ew_g6rA, acesso em 02 de agosto de 2010.
- Música Fractal. Disponível em: http://www.youtube.com/watch?v=B28_1EXilUI, acesso em 02 de agosto de 2010.
- Introdução à Geometria Euclidiana. Disponível em: http://pessoal.sercomtel.com.br/matematica/fundam/geometria/geo-basico.htm, acesso em 02 de agosto de 2010.
Avaliação
A avaliação deverá ser diagnóstica, processual e continua, ou seja, realizada ao longo de todas as aulas.
Critérios a serem observados:
- Participação na atividade inicial.
- Desenvolvimento e realização das atividades durante os questionamentos? Participou? Raciocínio adequado? O aluno foi argumentativo?
- Participação no desenvolvimento do contexto geral da aula.
- Na atividade do software. Participou? Produziu?
Sem estrelas 0 classificações
- Cinco estrelas 0/0 - 0%
- Quatro estrelas 0/0 - 0%
- Três estrelas 0/0 - 0%
- Duas estrelas 0/0 - 0%
- Uma estrela 0/0 - 0%
Denuncie opiniões ou materiais indevidos!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus




 Fractal Explorer
Fractal Explorer