22/10/2010
Edson Luis Nunes, Daniel Rodrigues Ventura, José Ângelo de Faria
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Educação de Jovens e Adultos - 1º ciclo | Estudo da Sociedade e da Natureza | Seres humanos e o meio ambiente |
| Ensino Médio | Física | Som, imagem e informação |
O que o aluno poderá aprender com esta aula
--Saber identificar a influência das características físicas das cordas nos modos de vibração.
--Conhecer as variáveis que quantificam essas características.
--Saber a relação entre essas variáveis.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Ondulatória (aspectos gerais), velocidade de propagação de ondas em cordas tensas e modos de vibração de cordas sonoras.
Estratégias e recursos da aula
Leve para sala de aula 4 cordas de sisal (ou seja, de mesmo material), 3 delas com 4 metros cada, e bem diferentes uma da outra. Uma deve ser bem fina. A outra de calibre intermediário e a última bem grossa. Mas, a quarta corda deve ser grossa igual a mais grossa delas porém possuir 5 metros de comprimento. Leve também uma trena e uma balança capaz de fazer medidas de massas de até 30 kg (ou então pese cada uma das cordas e forneça essa informação para eles). Faça então uma breve revisão sobre Propagação de ondas em cordas tensas e Modos de vibração de cordas sonoras, utilizando-se de perguntas e respostas. Esta revisão deve contemplar as Fórmulas 1 e 2. Prossiga então com a parte prática.
(Figura 1: Dedução da fórmula de frequência - Figura de autoria pessoal)
Atividade 1:
Amarre as 4 cordas nas grades das janelas, sendo as 3 de mesmo comprimento numa mesma janela e a maior em outra janela. Peça a 4 alunos que façam as cordas vibrarem no modo fundamental (primeiro harmônico). Agora peça aos demais alunos, observadores do processo, que comparem se há diferença no esforço que cada um dos 4 colegas faz. Eles dirão que sim. Pergunte então o porque. Se alguém responder certo parabenize-o. Caso isso não aconteça o professor deve pedir que observem as dimensões de cada corda, que 3 delas, apesar de possuírem o mesmo comprimento e serem de mesmo material, são de diâmetros bem diferentes. E a última, além de grossa é maior que as demais. Neste momento alguém já responderá que para agitar a corda maior e as mais grossas o esforço feito é maior que o esforço feito para agitar as mais finas que elas, e assim sucessivamente. Se necessário, mais detalhes sobre os harmônicos podem ser obtidos pelo professor na aula http://portaldoprofessor.mec.gov.br/verAula.html?aula=22280.
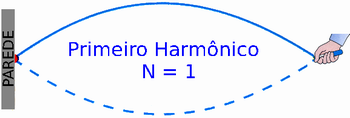
(Figura 2: Harmônico fundamental ou primeiro harmônico - Figura de autoria pessoal)
Atividade 2:
Bom, agora eles já possuem um norte para seguirem: as características físicas de cada corda. Então peça para que façam grupos de 5 pessoas e discutam qual seria a provável relação matemática entre a frequência de vibração f e as seguintes variáveis: comprimento L, diâmetro D, força tensora F e densidade absoluta μ. Deixe que discutam por no mínimo uns 10 minutos. Analise as respostas dos grupos. É bem provável que algum grupo chegará a alguma conclusão razoável, tal como: f é diretamente proporcional a F e inversamente proporcional D, L e μ.
Prossiga então com a parte teórica da aula. Diga que é aproximadamente isso, mas que a relação correta entre essas variáveis é dada pela Fórmula 3 apresentada na Figura 1. O professor, neste momento, usando o quadro, deve então fazer a dedução apresentada na Figura 1, onde se parte das Fórmulas 1 e 2 e chega-se à Fórmula 3, para que eles entendam a relação matemática exata entre as variáveis que descrevem as características físicas das cordas.
Atividade 3:
Peça agora, usando-se a mesma formação de grupos, para pesarem as cordas, medir seus comprimentos e determinar seus diâmetros e densidades absolutas. Usando essas informações eles devem montar uma tabela com o valor (calculado por eles) da força tensora F que deve ser aplicada em cada uma das cordas para que elas vibrem com o primeiro, segundo, terceiro e quarto harmônicos. Todos os alunos dos grupos devem anotar essa tabela nos seus cadernos. Terminados os cálculos parta para as conclusões finais da aula, a seguir.
Agora desfaçam os grupos e encerre a aula sintetizando o conhecimento adquirido. Pergunte a eles o que acontece com a frequência de vibração de uma corda quando se aumenta o seu comprimento ou a sua densidade absoluta, de acordo com o que eles observaram e calcularam. Certamente eles dirão, com facilidade, que a frequência diminui. E o que acontece quando se aumenta a força tensora da corda? Eles responderão, também facilmente, que a frequência aumenta.
Diga a eles que é este o processo que se utiliza para afinação de instrumentos de corda. Por exemplo, se eles observarem alguém afinando um violão verá que o que se faz é alterar a força tensora na corda para que esta atinja a frequência correta. O mesmo é válido para pianos, harpas, etc.
Recursos Complementares
Aprenda mais sobre cordas sonoras - frequências naturais de vibração em função de suas características físicas:
Cola da Web: http://www.coladaweb.com/fisica/ondas/ondas
UFS: http://www.fisica.ufs.br/CorpoDocente/egsantana/ondas/estacionarias/estacionarias.html
USP: http://www.eca.usp.br/prof/iazzetta/tutor/acustica/propagacao/vel_prop.html
NEWTON, V.B; HELOU, R.D.; GUALTER, J.B. Tópicos de Física 2 – Termologia, Ondulatória e Óptica. São Paulo: Editora Saraiva, Vol. 2, 448p., 18a Ed., 2007.
Avaliação
Elabore questões teóricas onde se pede apenas o que acontece com uma variável quando se varia outra. Mas elabore também questões que envolvam cálculos das frequências de vibração para várias cordas com características físicas diferentes.
Sem estrelas 0 classificações
- Cinco estrelas 0/0 - 0%
- Quatro estrelas 0/0 - 0%
- Três estrelas 0/0 - 0%
- Duas estrelas 0/0 - 0%
- Uma estrela 0/0 - 0%
Denuncie opiniões ou materiais indevidos!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus