25/10/2010
Edson Luis Nunes, José Marcelo Gomes, Daniel Rodrigues Ventura.
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Educação de Jovens e Adultos - 2º ciclo | Ciências Naturais | Visões de mundo |
| Ensino Médio | Física | Movimento, variações e conservações |
O que o aluno poderá aprender com esta aula
· Relacionar força com a mudança de direção da velocidade.
· Aplicar a segunda Lei de Newton em um movimento circular.
· Determinar a força resultante atuante em um móvel ao efetuar uma curva.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
· Leis de Newton, Movimento Circular Uniforme, Movimento Uniformemente Variado.
Estratégias e recursos da aula
http://i.ytimg.com/vi/7bFm4jJ8IAs/0.jpg
Sugerimos que o professor no início de sua aula apresente as figuras acima, Figura 01 e Figura 02 e argumente o tipo de trajetórias exercidas pelos móveis, aviões na Figura 01 e moto na Figura 02. O que é comum nas duas figuras é exatamente o tipo de trajetória descrita pelos móveis mostrada através das fotos, ou seja, em ambas os móveis descrevem trajetória curvas, no plano vertical, Figura 01 e no plano horizontal, Figura 02. O professor deve argumentar que quando a trajetória descrita pelo móvel é uma circunferência ou um arco da circunferência seu movimento naquele instante é um movimento circular. Se no momento em que o móvel executa a curva o módulo de sua velocidade não varia, seu movimento é circular uniforme e neste caso a força resultante que atua nele é a força centrípeta responsável pela variação da direção da velocidade.
Atividade I
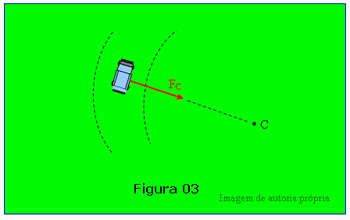
Depois o professor deverá mostrar a Figura 03 para os alunos, essa figura corresponde a um automóvel em movimento numa curva circular sendo a via plana e horizontal.
Repasse essas informações e Pergunte para que a turma responda oralmente: quais as forças que atuam no veículo no instante mostrado, segundo o esquema? Pergunte também qual a força resultante supondo que o módulo da velocidade permanece constante, durante o tempo em que o veículo realiza a curva?
· As forças que atuam no veículo no instante mostrado são: seu peso p, força de reação normal FN do solo sobre o veículo e a força de atrito fatr entre o asfalto e os pneus.
· A força resultante é a soma dessas forças; uma vez que a força de reação normal e o peso se anulam, porque elas tem mesma intensidade, mesma direção (vertical) e sentidos opostos, a resultante é igual a força de atrito. Em um MCU a força resultante equivale a força centrípeta, portanto a força centrípeta é igual a força de atrito (FC = fatr), FC representada na Figura 03.
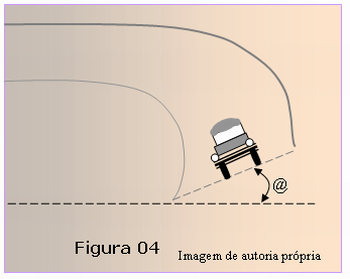
Após análise da Figura 03 o professor poderá mostrar a Figura 04 que também ilustra o momento em que um automóvel está percorrendo uma curva horizontal, porém a pista é inclinada de um ângulo @ conforme mostrado na figura.
Peça aos alunos que, desconsiderando o atrito entre os pneus e o solo, faça o diagrama de forças que atuam no carro. Depois utilizando o método do paralelogramo encontre o vetor resultante dessas forças. Pergunte para eles que força é essa.
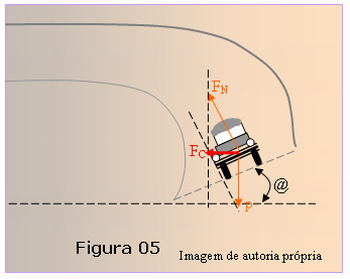
As respostas envolvendo as questões anteriores estão respondidas na Figura 05. Nela, há um esquema do diagramas de forças atuantes no carro, reação normal do solo sobre o carro, FN e o peso do carro, p. Também nesta figura está representada a soma das forças FN e p que é a força centrípeta FC, responsável pela mudança de direção da velocidade.
Atividade II
Após explicações das forças atuando no veículo da Figura 05 o professor poderá apresentar a Figura 06 que ilustra um pêndulo simples girando numa trajetória circular num plano horizontal cujo centro da trajetória está na vertical do ponto de equilíbrio do pêndulo. Peça aos alunos que usando uma folha de papel ou no próprio caderno façam o diagrama de forças que atuam no pêndulo e usando o método do paralelogramo determinar geometricamente a resultante dessas forças. Pergunte a eles; o que se pode concluir dessa força resultante considerando que o movimento do pêndulo seja circular e uniforme?
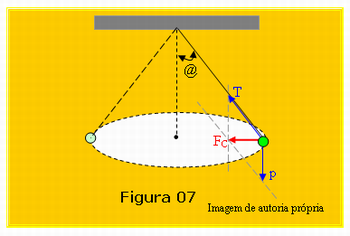
Após esperar alguns minutos para os alunos resolverem o problema, o professor então deverá apresentar a resolução do exercício mostrando a Figura 07. Nela está representado o diagrama de forças no pêndulo, T é a força de tração no fio e p é o peso do pêndulo. A soma usando o método do paralelogramo também se encontra nesta figura. O professor ainda deve explicar para a turma que a força resultante da soma de T e p, é a força centrípeta FC, uma vez que em um MCU a força resultante é a força centrípeta.
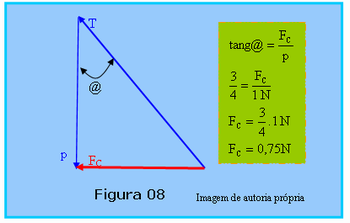
Peça aos alunos que mais uma vez faça a soma dos vetores T e p obtendo geometricamente a resultante, desta vez pelo método do polígono. Depois calcule o valor da Resultante, força centrípeta, considerando os seguintes valores: p = 1 N, cos@ = 0,8; sen@=0,6 e tan@ = 3/4.
A maneira mais simples para solucionar essa questão está sintetizada na Figura 08; o professor então deve mostrar essa figura aos alunos e lembrá-los que num triângulo retângulo a tangente de um ângulo é equivalente ao quociente do cateto oposto pelo cateto adjacente ao ângulo.
Atividade III
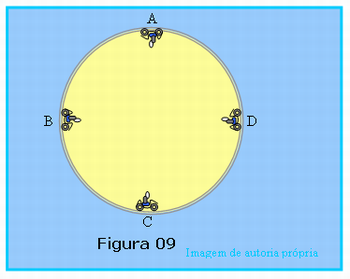
Em seguida o professor deverá apresentar para os alunos a Figura 09, projetando essa figura numa tela, ou poderá fazer um esquema semelhante no próprio quadro da sala de aulas. Essa figura esquematiza um motociclista girando dentro de um globo, portanto, numa trajetória circular, em um plano vertical, destacando-se 4 posições, momentos quando ele passa pelos pontos A, B, C e D. Após explicação da figura, distribua os alunos em equipes de no máximo 4 membros e peça aos alunos que nos pontos mostrados A, B, C e D, desconsidere a existência da força de atrito e represente as outras forças que atuam no conjunto moto e motociclista em cada um desses pontos. Considere que em cada ponto, inclusive em A, a velocidade é suficiente para fazer com que os pneus exercem pressão sobre a superfície de contato.
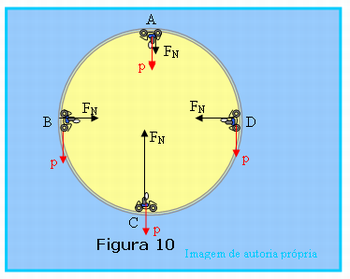
Depois que os alunos resolveram ou tentaram resolver o exercício, o professor então deverá explicar para a turma que sem atrito não há força dos freios nem do motor, restando a força peso, sempre presente nos corpos próximo a Terra e a força de reação normal da superfície sobre a qual os pneus apóiam. Depois, mostrar a Figura 10 em que nos pontos A, B, C e D, estão representadas as forças peso e reação normal. Observe que nos pontos B e D a resultante não é a força centrípeta porque nesses pontos além da força centrípeta responsável pela alteração da direção da velocidade, no ponto B a velocidade está aumentando e no ponto D a velocidade está diminuindo.
Depois, com as equipes ainda formadas o professor deverá perguntar como uma aeronave consegue fazer uma curva plana em MCU. Que força ou quais as forças é(são) responsável(responsáveis) pela força centrípeta no instante em que executa uma curva plana no ar em MCU?
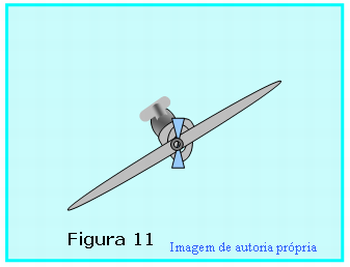
Depois de ouvir algumas respostas o professor deverá mostrar a Figura 11 que ilustra o instante em que um avião se inclina para efetuar uma curva plana em MCU, ou desenhar no quadro um esquema equivalente a ele. Peça aos alunos que representem graficamente as forças que atuam no avião e encontre geometricamente a resultante dessas forças.
Para correção do exercício o professor poderá mostrar a Figura 11 e explicar que além da força peso do avião, ele comprime o ar sobre o qual está apoiado, o ar então exerce no avião uma força de reação, representada nesta figura. A soma da força peso e reação normal do ar sobre o avião resultam na força centrípeta FC também representada esquematicamente na Figura 12.
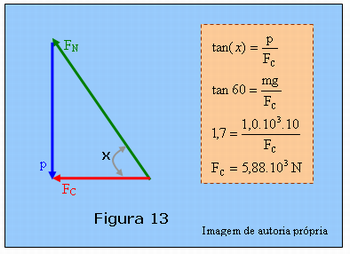
Para finalizar o professor poderá ainda propor o seguinte problema: Na Figura 12 suponha que a massa do avião seja de 1,0 tonelada incluindo a massa do piloto, x = 60 graus, qual o valor da força que faz com que o avião faça a curva plana e qual o raio da curva? Use g = 10 m/s2 e tan60 = 1,7.
Obs. Solução na Figura 13, abaixo.
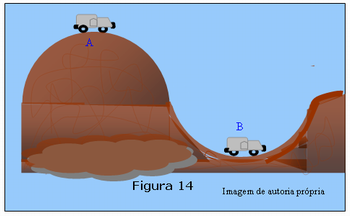
A Figura 14, abaixo é referente a um exercício proposto no espaço de avaliação.
Recursos Complementares
Sugerimos que o professor assista ao filme que se encontra no endereço abaixo e se for possível apresentar esse filme para a turma explicando porque tal acontecimento é possível. É um experimento sobre um rotor em miniatura, que imita aquele rotor que algumas vezes são encontrados em parques de diversão. O rotor consiste de um grande cilindro aberto com fundo móvel em que as pessoas ficam de pé recostadas na parede interna do cilindro. Este é colocado para girar e quando atinge certa velocidade seu fundo é deslocado para baixo ficando as pessoas suspensas com as costas grudadas na parede do cilindro. A força que comprime a pessoa na parede tem módulo igual a força centrípeta cujo valor varia com a velocidade de rotação do cilindro, velocidade angular w, FC = mw2R, em que m é a massa da pessoa e R o raio do cilindro. A força de atrito que vai equilibrar o peso é fatr = u.FC, u é o coeficiente de atrito entre a pessoa e a parede do cilindro. A partir de um determinado valor da velocidade, a força de atrito iguala ao peso da pessoa mantendo-a em equilíbrio vertical.
Mago da Física - ROTOR Miniatura: 4 min e 36 s
http://www.youtube.com/watch?v=XB3a4--GwHg
Avaliação
Os exercícios do texto são suficientes para avaliar a assimilação do conteúdo durante a aula pelos alunos, mas o professor ainda poderá elaborar exercícios para que os alunos resolvam em equipes ou individualmente, como exemplo segue o exercício abaixo.
Na Figura 14 do texto, traçar os vetores correspondentes às forças que atuam no veículo nos pontos A e B quando o veículo passa por uma lombada e por uma depressão da estrada respectivamente, considerando a velocidade do veículo constante e desprezando o atrito entre pneus e solo.
Quatro estrelas 1 classificações
- Cinco estrelas 0/1 - 0%
- Quatro estrelas 1/1 - 100%
- Três estrelas 0/1 - 0%
- Duas estrelas 0/1 - 0%
- Uma estrela 0/1 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Sandra Enoch, Portugal - disse:
sandra_enoch@yahoo.com24/11/2010
Quatro estrelasGostei. Simples e clara. Fique em paz SE
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus