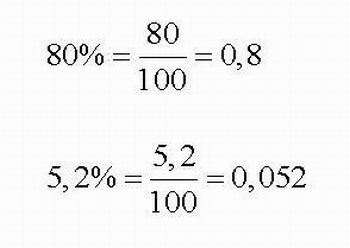13/10/2010
Edite Resende Vieira, Fernando Celso Villar Marinho, Jackson Lopes, Raquel Cupolillo Simões de Sousa, Rita Maria Cardoso Meirelles, Victor Cesar Paixão Santos
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Análise de dados e probabilidade |
O que o aluno poderá aprender com esta aula
Conceitos de razão centesimal, porcentual e decimal;
Transformar números racionais em taxas percentuais e vice e versa;
Ler e interpretar taxas percentuais.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Reconhecimento e operação com frações.
Números decimais (escrita e operações).
Porcentagem (noções e transformações).
Estratégias e recursos da aula
A compreensão e o reconhecimento das taxas percentuais é algo muito importante no estudo da matemática financeira, assim como apresentar ao aluno o uso da notação decimal, pois em alguns momentos sua utilização poderá facilitar cálculos e o estabelecimento de conjecturas. Esse estudo também será importante para dar inicio ao estudo dos juros simples e compostos.
Atividade 1
Essa atividade exploratória tem por objetivo principal estimular o desenvolvimento da habilidade de pesquisa e síntese dos alunos.
Sugira que os alunos em grupo, pesquisem inicialmente em alguns sites do tipo:
Cada grupo fará a pesquisa num endereço diferente e você, professor, irá propor alguns questionamentos como estes:
- Como transformar uma fração em um número escrito na notação decimal?
- É sempre possível escrever um número decimal na forma de fração decimal?
- O que é número misto?
- Como a porcentagem 325% pode ser escrita na forma de número misto?
Depois, distribua entre os alunos cartolinas e peça para eles utilizarem a criatividade para preparar um resumo sobre o que entenderam e socializar o resultado com os demais colegas de classe. Neste momento o professor anotará os aspectos negativos e positivos e as conclusões coincidentes, que se estiverem corretas, deverão ser reforçadas.
Atividade 2
Solicite aos alunos que registrem as informações referentes a taxas percentuais presentes no vídeo. Com os registros estimule a discussão acerca do que seria a porcentagem.
Obs: É possível e esperado que os alunos digam que é uma parte ou uma quantidade de algo. Sendo assim, o que eles precisam saber é que estão corretos, porém a porcentagem é a fração que indica esta quantidade, mas escrita na forma de fração equivalente com o denominador 100.
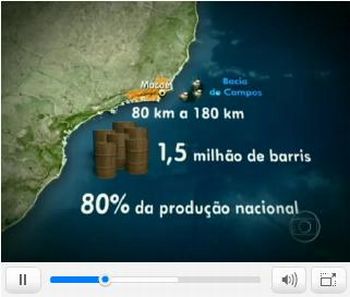
Exiba o vídeo com a reportagem "Nova proposta para pré-sal desagrada produtores" exibida no dia 11/03/2010, no Jornal Nacional (TV Globo), como motivação para abordar o conteúdo em questão e promover uma discussão acerca do percentual que caberia a um determinado estado ou município.
Imagem Inicial Imagem em destaque
Destaque o seguinte trecho da reportagem: " A extração média diária na Bacia de Campos é de 1,5 milhão de barris, 80% da produção nacional. "
Solicite aos alunos para escreverem a quantidade 1,5 milhão utilizando apenas numerais. Essa "tradução" nem sempre é fácil para eles!
Introduza a notação para forma porcentual, ou seja, apresente ao aluno que a fração de denominador 100 pode ser escrita de outra forma: anotando-se o numerador da razão seguido do símbolo % (por cento).
Os exemplos que seguem, servem para ilustrar esta situação:
Obs.: Diga aos alunos que a fração também pode ser chamada de razão centesimal, razão porcentual, índice ou taxa porcentual.
Peça aos alunos que reescrevam as seguintes razões não centesimais na forma centesimal:
a) 4 em cada 10
b) 7 em cada 10
Atividade 3
Seguindo com as transformações e com as várias formas de apresentar uma taxa percentual, também é importante apresentar a passagem da razão porcentual para a forma decimal. Sendo assim, a forma unitária da razão b/100 é o número decimal que obtemos ao dividir b por 100.
Exemplos:
Quando tratamos do estudo de taxas percentuais é importante chamar a atenção dos alunos quanto ao período ao qual a taxa está sendo aplicada. Por exemplo, é possível realizar aplicações por um mês a taxa de 0,5% a.m. ( ao mês ) ou aplicar a mesma quantia a taxa de 0,15% a.t. ( ao trimestre ), porém dependendo da forma de tributação (juros simples ou compostos) o rendimento pode variar. Ressalte e apresente, também, as seguintes nomenclaturas:
a.m.: ao mês
a.t.: ao trimestre
a.s.: ao semestre
a.p.: ao período
a.a.: ao ano
Atividade 4
Neste momento de identificação de taxas percentuais, é válido apresentar o conceito de taxas negativas. Exiba a imagem abaixo onde aparecem taxas com sinal negativo. Estimule os alunos a argumentarem sobre o que eles acreditam representar estas taxas, na esperança de que percebam que o sinal negativo significa decréscimo de um determinado valor.
Peça aos alunos que determinem quanto estava custando o dólar (em reais) antes do decréscimo?
Seja D o valor do dólar antes do decréscimo de 0,31%. Sendo assim,
D x ( 1 - 0,31% ) = 1,7
D x ( 1 - 0,0031) = 1,7
D = 1,7053
Atividade 5
Proponha aos alunos que analisem a seguinte situação e identifiquem a taxa de decréscimo aplicada:
“Um automóvel que foi adquirido por R$ 30 000,00, está sendo vendido a R$ 25 000,00. Calcule o percentual de depreciação no valor de venda do veículo.”
Se o bem foi adquirido por R$ 30 000,00 e vendido por R$ 25 000,00, houve prejuízo de R$ 5 000,00 na transação. Sendo assim, 5000 : 30 000 = 0,17 = 17% , ou seja, a depreciação no valor do bem foi de 17%.
Atividade 6
Dando continuidade ao estudo das taxas, porém visando ao inicio do estudo dos juros, apresente o conceito de fator de correção propondo o problema abaixo
" Calcule o preço de uma mercadoria que sofreu um aumento de 15%. "
Para tal, o aluno deverá multiplicar o preço original por 1,15, já que P + 15% de P = P + 0,15P = (1 + 0,15) x P = 1,15 x P.
Neste caso, a taxa percentual é de 15%, que é frequentemente representada por i = 0,15, e o fator 1 + i = 1,15.
http://www.projetofundao.ufrj.br/matematica/images/stories/matfin.jpg
Aproveite a situação-problema da atividade 5 para trabalhar também o fator de correção que, dependendo do caso será de aumento ou de desconto:
Atividade 7
Jogo do Fator de Correção
Divida a turma em dois grupos e os organize em duas filas indianas (um a frente do outro). Você será o juiz. Cada grupo deverá fazer uma afirmação correspondente a um aumento ou um desconto e o grupo oponente terá que dizer qual o fator de correção. Após algumas rodadas peça para eles dizerem o Fator de Correção e o grupo adversário terá que advinhar a afirmação correspondente.
Por exemplo:
| Afirmação |
Fator de Correção |
| Aumento de 15% |
(1+0,15)=1,15 |
| Desconto de 20% |
(1-0,20)=0,8 |
Cada resposta certa corresponde a um ponto para o grupo que respondeu corretamente. Respostas erradas dão ponto para o grupo adversário. As perguntas e respostas devem ser rápidas.
Aproveite esta atividade para avaliar os alunos.
Recursos Complementares
Acesso aos links:
Grupo de Matemática Financeira - Projeto Fundão
http://www.projetofundao.ufrj.br/matematica/index.php?option=com_content&task=view&id=6&Itemid=18
Avaliação
Dividir a turma em dois grupos — meninos x meninas — para que calculem o percentual de meninos e o percentual de meninas na turma. Após o cálculo do percentual, peça que calculem o quanto deveria diminuir em determinado grupo (em percentual) para que os dois grupos ficassem iguais.
Outra opção é aproveitar a atividade 6 para avaliar o desempenho dos alunos.
Quatro estrelas 2 classificações
- Cinco estrelas 1/2 - 50%
- Quatro estrelas 1/2 - 50%
- Três estrelas 0/2 - 0%
- Duas estrelas 0/2 - 0%
- Uma estrela 0/2 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Aldo Silva, Escola Movimento , Pernambuco - disse:
aldofirefighter@gmail.com27/10/2011
Cinco estrelasMuito bom e didático.
-
Indiara Nunes, U F Sta Maria-Pólo de Cachoeira do Sul , Rio Grande do Sul - disse:
indiaranunes631@gmail.com13/10/2010
Quatro estrelasAcredito que esta aula é muito atrativa pois nela são oferecidas várias opções de aprendizado,com enfase nas frações,no que elas realmente representam,para só então serem abordados de maneira bastante proveitosa conteúdos referentes à probabilidade.Os vídeos foram escolhidos com o intuito claro de fazer com que uma aula bastante cansativa se transforme em momento de apreensão prazeirosa do comhecimento.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus