24/10/2010
Fernando Celso Villar Marinho, Rita Maria Cardoso Meirelles, Jackson Lopes, Raquel Cupolillo Simões de Sousa, Edite Resende Vieira, Armando Tramontano
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Álgebra |
O que o aluno poderá aprender com esta aula
- Identificar a imagem de uma função através de seu gráfico;
- Obter a imagem de uma função composta a partir da análise dos gráficos de suas funções componentes;
- Elaborar uma estrutura de passos seqüenciais para obtenção do elemento imagem em uma composição de funções.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
- Identificar o plano cartesiano e seus eixos como representações gráficas de conjuntos;
- Reconhecer a função como uma relação particular entre dois conjuntos;
- Manipular algebricamente a composição de funções.
Estratégias e recursos da aula
Caro professor, a proposta aqui apresentada é baseada em atividade disponível no site do Projeto Novas Tecnologias no Ensino (http://www.dmm.im.ufrj.br/projeto/projetoc/precalculo/index.htm) utilizando a ferramenta Descartes, desenvolvida pelo Proyecto Descartes (http://descartes.cnice.mec.es). Este aplicativo e suas atividades são regulados pela licença de uso “Creative Commons” (http://creativecommons.org/licenses/by-nc-sa/2.5/es/deed.pt).
Esta aula deverá ser realizada em um Laboratório de Informática. As atividades exploratórias podem ser feitas em duplas ou trios e, neste caso, deve ser estimulado o diálogo entre os componentes de cada grupo, o que tende a promover uma construção coletiva do conhecimento, a partir das observações e trocas de experiências entre os colegas.
Sempre que possível, cabe debater com toda a turma o que cada grupo pôde observar. Isto pode servir ao professor, inclusive, como um dos critérios para aferir o real aprendizado dos alunos, a título de avaliação diagnóstica da turma e de cada indivíduo.
Atividade 01 - Operando com Funções
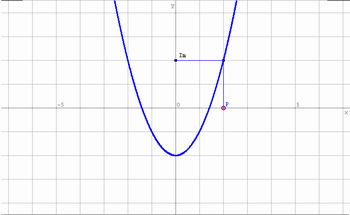
Utilize o recurso da ferramenta Descartes em http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/ComposicaoDeFuncoesAtravesDaAnaliseGrafica01.html para explorar com os alunos as conseqüências das operações com funções em termos gráficos. Observe:
Inicialmente, mostre aos alunos utilizando o gráfico acima que, para cada valor no eixo x, temos um correspondente no eixo y, relacionado ao gráfico da função. Informe a eles que o conjunto de pontos do eixo y que possuem um correspondente no eixo x é o que chamamos “Conjunto Imagem” da função. Este conceito de imagem é importante no processo de composição de funções, dado que em uma composição o Domínio da segunda função deve estar contido no Conjunto Imagem da primeira.
Faça os alunos notarem, utilizando o recurso relacionado no início desta seção, que a coordenada y do gráfico da função f(x) + g(x) é a soma das coordenadas y de f(x) e g(x), para um mesmo x. Formalmente falando, para cada x0, temos que uma função h(x) = f(x) + g(x) satisfaz h(x0) = f(x0) + g(x0).
O segundo passo desta atividade mostra dois exemplos bem interessantes.
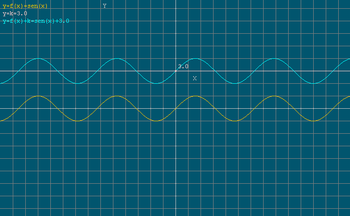
No primeiro, vamos somar uma função constante à função sen(x). Quando somamos uma função f a uma função constante g, o gráfico da f é simplesmente deslocado verticalmente. Neste caso particular, onde a função f é sen(x), este gráfico passa a “envolver” o gráfico da função constante. Observe:
Isto ocorre devido ao fato de que o seno varia de -1 a 1. Assim, ao somar o seno a uma função constante, tudo que estamos fazendo é somar um número (fixo, neste caso) ao seno; e, dependendo do valor de x considerado, a constante pode ser acrescida de até uma unidade, decrescida de até uma unidade, ou nada ocorrerá (caso em que o seno é zero). Com isto, o gráfico do seno não pode “se afastar” do gráfico da função constante.
Se realizarmos o mesmo procedimento, agora utilizando uma função do primeiro grau, ao invés de uma função constante, o efeito será o mesmo:
É importante mostrar aos alunos que, neste caso, o gráfico de x + sen(x) tem a oscilação característica do seno, no entanto em torno da reta descrita por y = x. Isto ocorre devido ao fator somado ao seno para cada valor x0, analogamente ao que ocorrera para a função constante.
Para Reflexão da Turma
Note ainda que este comportamento não é compartilhado por funções de graus superiores, cujo valor é rapidamente muito superior ao do seno, de modo que este interfere muito pouco em seus gráficos. Desafie a turma a justificar o motivo que faz com que o gráfico do seno não se comporte do mesmo modo com funções de graus maiores ou iguais a 2.
Atividade 02 - Composição de Funções em Biologia
Leve os alunos a analisarem o seguinte problema (adaptado do originalmente publicado em http://www.dmm.im.ufrj.br/projeto/projetoc/precalculo/sala/Atividades/capitulos/comp12.html):
“Um biólogo está analisando a população de uma espécie de peixe nas águas de um canal. Ele está interessado em estudar a variação da reprodução destes animais durante 10 semanas. Por estudos de laboratório, ele sabe que a temperatura da água influi na reprodução desta espécie. A Tabela 1 nos mostra como se dá essa dependência.
| ºC |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
| Crias |
1.3 |
1.5 |
1.7 |
2.0 |
2.3 |
2.6 |
2.9 |
2.8 |
2.7 |
2.6 |
2.4 |
2.3 |
2.2 |
2.0 |
1.8 |
1.5 |
1.1 |
(Tabela 1: Temperatura da Agua em ºC e Média de Crias por Fêmea e Dia)
Durante 10 semanas, o biólogo mediu a temperatura média da água do canal. A Tabela 2 nos mostra os resultados obtidos.
| Semana |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| ºC |
13 |
14 |
15 |
17 |
20 |
18 |
21 |
25 |
22 |
18 |
(Tabela 2: Semana e Temperatura da Água em ºC)
Combinando as duas tabelas, o biólogo pode averiguar o número médio de crias, por fêmea e dia, no canal, durante essas dez semanas e decidir qual o melhor momento . Para isso, basta organizar os dados coletados nas duas tabelas. Faça uma nova tabela, que considere a semana e a média de crias por fêmea e dia, para descobrir quais foram as três semanas mais favoráveis à reprodução desse peixe.”
OBS.: A solução encontra-se no final desta aula.
Na página citada como referência há uma tabela adicional, que pode ser preenchida com as respostas e verificada. Em um laboratório de informática, é possível fazer com que os alunos realizem a tarefa e escrevam seus resultados na tela, clicando a seguir no botão "Comprovar", onde poderão verificar se suas respostas estão corretas.
Este é um bom momento para incentivar os alunos a procurarem outros casos cotidianos que envolvam este tipo de operação composta; por exemplo: “Quanto foi gasto por um aluno com lanche em cada semana de aula, em função do biscoito/bolacha comprado e sabendo que cada tipo deles possui um preço diferente?”
Atividade 03 - Compondo Funções a Partir de Gráficos
As atividades anteriores devem auxiliar o aluno a compreender o efeito que operações com funções podem ter do ponto de vista gráfico, e ainda estabelecer um processo intuitivo acerca da composição como uma “seqüência de passos encadeados”, onde o segundo passo depende diretamente do resultado do primeiro, e assim por diante.
Em seguida, os alunos devem estar prontos a interagir com uma atividade que visa conduzir a turma a construir um procedimento de composição de funções a partir dos gráficos das funções componentes.
Utilize o recurso da ferramenta Descartes em http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/ComposicaoDeFuncoesAtravesDaAnaliseGrafica02.html para percorrer o procedimento de composição de funções a partir de seus gráficos.
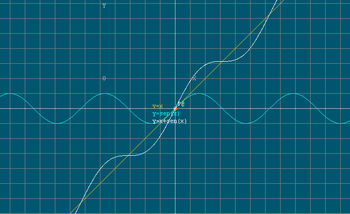
Nele, são consideradas as funções f(x) = x2 e g(x) = 2x + 1. São definidos 6 passos para encontrar a função composta graficamente, além de um 7º passo que visa encontrar a expressão algébrica da composta e compará-la com o resultado obtido graficamente. Os passos, resumidos aqui, são:
Preparação: Traçar o gráfico das duas funções. Para obter h(x) = g(f(x)), temos que traçar o gráfico de g(x) e de f(x).
- Traçar o gráfico auxiliar de y = x. Ele será bastante útil, uma vez que serve para “transferir” as coordenadas de um eixo a outro. Por exemplo, ao termos um ponto de ordenada 3 sobre o gráfico de f(x), podemos encontrar no eixo x o ponto de abscissa 3 facilmente, fazendo a imagem inversa do ponto (0,3) em relação a y = x, donde obtemos (3,0).
- Usando y = x encontramos no eixo das abscissas o correspondente ao valor de f(x). Este será o valor a ser inserido na função g.
- Usando o valor encontrado, utilizar o gráfico de g(x) para obter a sua imagem, isto é, o valor de g(f(x)).
- Este ponto é um ponto do gráfico de h(x) = gof(x).
- Para traçar o gráfico da gof, é possível modificar o valor do parâmetro x, e teremos uma família de pontos marcados na cena. Todos os pontos marcados pertencem ao gráfico de h(x).
- Encontre a expressão algébrica para a função gof e verifique se o gráfico obtido condiz com a expressão encontrada algebricamente.
Composição de Funções em Biologia: semana 1 = 1.5, semana 2 = 1.7, semana 3 = 2.0, semana 4 = 2.6, semana 5 = 2.7, semana 6 = 2.9, semana 7 = 2.6, semana 8 = 2.0, semana 9 = 2.4, semana 10 = 2.9.
Recursos Complementares
DESCARTES. Página do Projeto. http://descartes.cnice.mec.es/
SANTOS, A.R. (coord.) Introdução às Funções Reais. Projeto Novas Tecnologias no Ensino. Instituto de Matemática, UFRJ. http://www.dmm.im.ufrj.br/projeto/projetoc/precalculo/index.htm
SEGADAS, C. et al. Desalgebrizando o Estudo de Funções Compostas. Anais do IX Encontro Nacional de Educação Matemática. Disponível em http://www.sbem.com.br/files/ix_enem/Minicurso/Trabalhos/MC03626583740T.doc
Avaliação
A avaliação, de caráter diagnóstico e objetivando o desenvolvimento do aluno, pode ser executada ao longo da atividade, em observância aos seguintes pontos:
- Participação ativa do aluno na parte da aula em que ele deve buscar no cotidiano exemplos de composição de funções;
- Verificação de aprendizado através de observação pelo professor dos experimentos realizados em cada etapa da aula. O professor deve inferir (se necessário através de perguntas à classe) se os grupos de fato compreenderam o que lhes foi solicitado em cada etapa, pois cada fase da atividade depende logicamente de um correto entendimento da etapa anterior.
Sem estrelas 0 classificações
- Cinco estrelas 0/0 - 0%
- Quatro estrelas 0/0 - 0%
- Três estrelas 0/0 - 0%
- Duas estrelas 0/0 - 0%
- Uma estrela 0/0 - 0%
Denuncie opiniões ou materiais indevidos!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus