06/12/2010
Rita Maria Cardoso Meirelles, Fernando Celso Villar Marinho, Jackson Lopes, Raquel Cupolillo Simões de Sousa, Edite Resende Vieira, Armando Tramontano
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Fundamental Final | Matemática | Números e operações |
| Ensino Fundamental Inicial | Matemática | Números e operações |
| Educação de Jovens e Adultos - 1º ciclo | Matemática | Números e operações |
O que o aluno poderá aprender com esta aula
- Relacionar a multiplicação de dois números inteiros à adição de parcelas repetidas;
- Relacionar operações de crédito e débito financeiro aos números inteiros;
- Estabelecer comparação entre a multiplicação de inteiros e o deslocamento sobre a reta numérica;
- Analisar a “regra de sinais” através dos padrões provenientes da interpretação da multiplicação como soma de parcelas repetidas.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
- Identificação dos números inteiros;
- Operação de soma de números inteiros;
- Multiplicação de números naturais.
Estratégias e recursos da aula
Caro professor: o processo de aprendizagem dos fundamentos da multiplicação entre números inteiros e suas propriedades representam um ponto de grande dificuldade por parte de muitos alunos do Ensino Fundamental. Por este motivo, consideramos importante a reflexão sobre alternativas para o ensino de alguns assuntos-chave para a construção de conhecimentos, habilidades e competências acerca das operações fundamentais com números inteiros. Em particular, esta aula tem por objetivo tratar da multiplicação destes.
Esta aula é composta de três momentos, onde poderão ter contato com atividades que os conduzirão até a conhecida "regra de sinais".
No primeiro, os alunos chegarão a ela a partir do processo que define a multiplicação: a soma de parcelas iguais. No segundo, eles serão levados a refletir sobre o significado dos sinais em operações de débito e crédito. No terceiro, eles terão acesso a um processo gráfico, utilizando a reta numérica dos inteiros, que permite chegar visualmente até a "regra".
Todas podem ser realizadas em sala de aula, com auxílio de um data-show para a terceira parte. Nesta terceira parte - que também pode ser realizada em um ambiente de laboratório de informática, possibilitando a exploração por parte dos alunos -, foi utilizado o mathlet Descartes - aplicativo que roda diretamente no navegador web, está disponível em http://descartes.cnice.mec.es e é regido pela licença "Creative Commons" (http://creativecommons.org/licenses/by-nc-sa/2.5/es/deed.pt).
Atividade 01
Adição de Parcelas Iguais
O processo de multiplicação nada mais é do que uma especialização de um processo já conhecido dos alunos aos quais esta aula se destina: a soma de dois ou mais números inteiros. Neste caso específico, estamos falando na soma de parcelas iguais. Tendo contato com a multiplicação através desta soma, o estudante pode compreender – ou estabelecer uma conexão que os levará a compreender – algumas regras consideradas "complicadas" por parte dos alunos de Matemática.
Reserve cerca de 15 minutos da aula para esta atividade. Inicialmente, introduza com a turma o tema "multiplicação" recordando a multiplicação de números naturais. Estão incluídas aí as idéias sobre "o que é a multiplicação de dois números" e a notação necessária:
- Multiplicar dois números nada mais é do que, dado o primeiro número, somá-lo repetidas vezes (quantidade esta dada pelo segundo número);
- Usamos a notação A x B para indicar a "multiplicação de A por B", isto é, A + A + A + ... + A, onde A é somado B vezes. Exemplo: 3 x 4 = 3 + 3 + 3 + 3 (quatro vezes).
Agora considere a soma, já conhecida pelos alunos, “2 + 2 + 2 = 6”; ela representa, como vimos, a multiplicação “2 x 3 = 6”.
Partindo deste exemplo, a tabela abaixo mostra que, uma vez que a multiplicação “2 x 4” consiste em, simplesmente, adicionar mais um fator "2" à soma, e que a multiplicação “2 x 2” consiste em retirar um fator "2" da mesma soma, podemos estabelecer uma relação entre a seqüência de somas/subtrações e a seqüência dos produtos (na verdade um esboço de tabuada):
| 2 x 5 |
8 + 2 = 10 |
| 2 x 4 |
6 + 2 = 8 |
| 2 x 3 |
6 |
| 2 x 2 |
6 - 2 = 4 |
| 2 x 1 |
4 - 2 = 2 |
(Tabela 1)
Leve os alunos a notarem que, a cada "2" incluído ou retirado, o resultado da multiplicação é acrescido ou decrescido de duas unidades.
Observe que, se continuarmos esta seqüência de modo decrescente, obtemos:
| 2 x 1 |
2 |
| 2 x 0 |
2 - 2 = 0 |
| 2 x (-1) |
0 - 2 = -2 |
| 2 x (-2) |
-2 - 2 = -4 |
| 2 x (-3) |
-4 - 2 = -6 |
(Tabela 2)
Com isto podemos observar que (+2) x (-3) = (-6), o que fornece aos alunos um indício de que ao multiplicarmos um número positivo por um número negativo, teremos como resultado um número negativo.
Dado que, na multiplicação, a ordem dos fatores não altera o produto, podemos escrever (+2) x (-3) = (-3) x (+2), e realizar o mesmo procedimento descrito anteriormente: uma progressão decrescente do fator multiplicador. Veja:
| (-3) x 2 |
-6 |
| (-3) x 1 |
-6 - (-3) = -6 + 3 = -3 |
| (-3) x 0 |
-3 - (-3) = -3 + 3 = 0 |
| (-3) x (-1) |
0 - (-3) = 0 + 3 = 3 |
| (-3) x (-2) |
3 - (-3) = 3 + 3 = 6 |
(Tabela 3)
Desta forma, observamos que (-3) x (-2) = (+6), o que fornece aos alunos um indício de que ao multiplicarmos um número negativo por outro número negativo, teremos como resultado um número positivo.
Com os exemplos expostos acima, o aluno será conduzido à conhecida "regra de sinais":
| (+) x (+) |
(+) |
| (+) x (-) |
(-) |
| (-) x (+) |
(-) |
| (-) x (-) |
(+) |
(Tabela 4)
Atividade 02
Débito x Crédito
Nesta atividade, os alunos terão contato com operações financeiras de débito e crédito, no âmbito do saldo de uma conta-corrente. Com isto, poderão perceber relações entre os sinais (+ e -) e as alterações que o saldo de uma conta sofre por intervenção de saques, depósitos, compras, etc.
Reserve de 20 a 25 minutos para esta atividade. Peça que os alunos se dividam em 3 grupos, que representarão as seguintes "pessoas": Comprador, Vendedor e Banco. Depois, entregue para cada grupo uma folha de papel com uma linha dividindo-a em duas colunas onde constem as expressões "Crédito/Entrada" e "Débito/Saída", respectivamente. Um modelo pode ser baixado em http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/MultiplicandoInteiros-DebitoCredito.pdf
Peça que cada um escreva no espaço "Saldo Inicial" o valor de R$ 10.000. A seguir, dê-lhes algumas operações para executar, sempre lembrando de expressá-las utilizando números inteiros; por exemplo:
- O Comprador adquire R$ 50 em mercadorias do Vendedor;
- O Vendedor pega R$ 200 no Banco;
- O Comprador faz uma dívida de R$ 150 com o Banco;
- O Comprador paga a dívida ao Banco em 3 x de R$ 60;
- O Vendedor paga R$ 150 ao Banco, quitando parte de sua dívida;
- O Comprador faz três saques de R$ 50 junto ao Banco;
- (crie outras situações e operações para os alunos).
Proponha situações que envolvam cada "personagem" pelo menos 10 vezes, para ter um volume de operações a executar. Ao final, peça que os grupos façam o cálculo para obter o saldo final de cada um (Comprador, Vendedor e Banco), levando em conta o sinal apropriado (+ e -). Ocorrências que tenham multiplicação devem entrar no "extrato" de uma vez só (por exemplo, deve ir para o extrato "3 x 60 = 180" e não três lançamentos de "60").
Leve os alunos a descobrirem quando usamos o sinal (+) para representar uma operação e quando usamos o sinal (-). Mostre a eles ainda que, ao fazermos um pagamento do Comprador ao Vendedor, temos um crédito em um deles e um débito no outro, e que cada um corresponde a um sinal distinto, de modo que nenhum dinheiro "desapareça" durante a transação.
Faça ainda com que os alunos percebam que, por exemplo ao realizar 3 saques de R$ 50, a operação que estamos executando sobre o Banco é 3 x (-50), e não -3 x 50; embora o resultado de ambas seja o mesmo, a natureza da operação é diferente. Leve isso em consideração também no momento de avaliar os registros dos alunos.
Em alguns casos você pode inserir um valor correspondente a juros nos cálculos (como no exemplo, em que o Comprador faz uma dívida de R$ 150 mas paga R$ 180 ao Banco). No entanto, não se preocupe em calcular juros exatos ou percentuais de juros, pois este não é o foco principal da atividade. Caso julgue apropriado, você pode na seqüência a esta aula trabalhar com os temas "Porcentagem" e "Juros", e retornar a esta atividade como exemplo motivador.
Como critério de avaliação, você pode pedir que cada aluno faça um novo "extrato", individualmente. Agora ele próprio deve definir o saldo inicial (não necessariamente iguais) dos três personagens, elaborar os eventos, transcrevê-los, representar as operações aritméticas, efetuá-las e calcular o saldo final. Dê aos alunos cerca de 5 minutos, com cada personagem tendo 5 ocorrências associadas a ele.
Atividade 03
A Reta Numérica dos Inteiros
Nesta atividade, temos outra analogia que pode ser criada no intuito de exprimir a relação entre os sinais de uma multiplicação e o sinal do produto: pensar a multiplicação como um deslocamento sobre uma reta numérica. As "regras do jogo" são bem simples:
- O tamanho do deslocamento é igual ao produto dos dois números sem o sinal;
- Multiplicar por (+) mantem o sentido do deslocamento;
- Multiplicar por (-) produz um deslocamento em sentido contrário.
Isto pode ser analisado no recurso utilizando o mathlet Descartes em http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/MultiplicandoNumerosInteiros01.html.
Reserve cerca de 10 minutos para esta atividade. Peça aos alunos que experimentem, utilizando o recurso com diferentes valores, e vejam o que ocorre em cada caso. Um resumo dos casos existentes podem ser vistos a seguir.
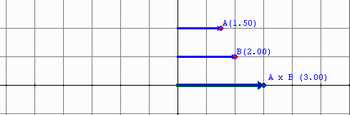
Ao realizar uma multiplicação A x B para valores positivos de A, os alunos podem observar duas situações distintas:
1ª) Quando B é igualmente positivo, o deslocamento é realizado no mesmo sentido que o deslocamento referente ao valor A; portanto, o produto é positivo. Veja:
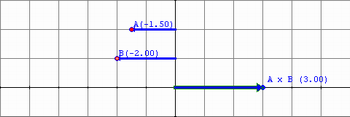
2ª) Quando B é negativo, o deslocamento é realizado no sentido contrário ao deslocamento referente ao valor A. Como A é positivo, esse deslocamento torna o produto negativo. Observe:
Já quando temos valores negativos de A, os alunos podem ver que o deslocamento original é realizado no sentido contrário ao citado anteriormente. Deste modo, as situações relacionadas acima terão sinais distintos:
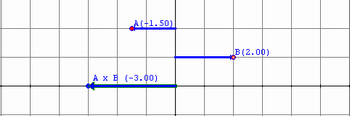
3ª) Quando B é positivo, o deslocamento é realizado no mesmo sentido de A; sendo A negativo, o produto é negativo. Por exemplo:
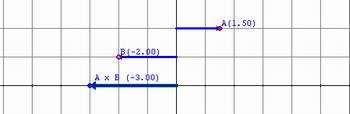
4ª) Quando B é negativo, o deslocamento é realizado no sentido contrário ao de A; sendo A negativo, o produto torna-se positivo. Assim:
Como é possível observar, o sinal de menos em B sempre altera o sinal do produto em relação ao sinal de A. Por isso temos que (-) x (-) = (+), por exemplo.
Observação
Cabe citar que estas abordagens não excluem de forma alguma quaisquer outras abordagens que você, professor, possa vir a utilizar. São, na verdade, novas perspectivas e possibilidades para o ensino do processo multiplicativo de números inteiros e da "regra de sinais".
Recursos Complementares
DESCARTES. Página do Projeto. http://descartes.cnice.mec.es/
Avaliação
A avaliação deve ser diagnóstica e permear toda a atividade.
O professor pode, ao longo das atividades ou de modo complementar, solicitar aos alunos que:
- dêem exemplos concretos de operações de multiplicação de números inteiros;
- desenhem em seus cadernos a reta numérica dos inteiros e realizem operações de multiplicação usando a idéia de deslocamento, como na Atividade 03;
- produzam uma nova simulação de movimentação de conta-corrente, nos moldes do observado na Atividade 02, escrevendo um extrato especificando o saldo inicial, os créditos e débitos e o saldo atualizado. Neste modelo de avaliação, leve em conta os registros dos alunos, se expressaram corretamente as operações aritméticas realizadas e se encontraram os resultados desejados.
Cinco estrelas 1 classificações
- Cinco estrelas 1/1 - 100%
- Quatro estrelas 0/1 - 0%
- Três estrelas 0/1 - 0%
- Duas estrelas 0/1 - 0%
- Uma estrela 0/1 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Arilza, SEEDUC , Rio de Janeiro - disse:
arilzavieira@gmail.com28/04/2015
Cinco estrelasMuito bem exemplificado comparando produto com soma, bem como demonstrando geometricamente
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus