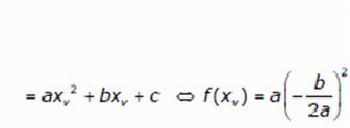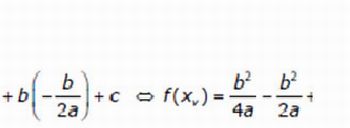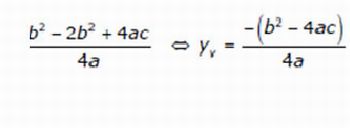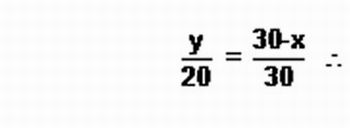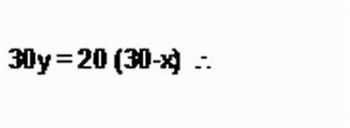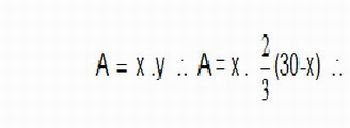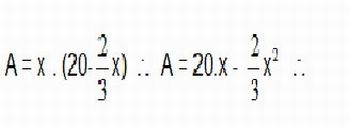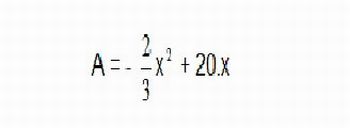09/11/2010
Armando Tramontano; Edite Resende Vieira; Fernando Celso Villar Marinho; Rita Maria Cardoso Meirelles; Victor Paixão
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Tecnologia para a matemática |
| Ensino Médio | Matemática | Álgebra |
O que o aluno poderá aprender com esta aula
Pesquisar e analisar onde a função quadrática pode ser aplicada no cotidiano;
Relacionar área de um triângulo com a função quadrática;
Trabalhar os conceitos de vértice e sinal da função;
Relacionar o sinal do delta com o número de raízes.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Função Quadrática – Estudo do foco, diretriz e eixo de simetria.
Função Quadrática – Conceito de vértice
Semelhança de triângulos
Intervalos reais
Estratégias e recursos da aula
Caro Professor, apresentaremos agora uma sugestão de sequência didática. Adaptá-las à realidade da sua escola e ao perfil de sua turma é o ponto de partida para a realização de um ótimo trabalho.
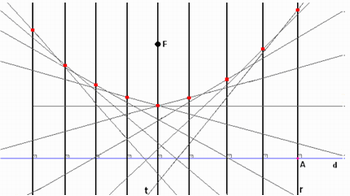
Atividade 1: Construção da Parábola Através da Dobradura
Nesta etapa os alunos irão trabalhar em grupos em sala de aula e irão verificar a formação da parábola a partir da reta diretriz e do foco. Esta atividade foi adaptada de [MACH 2007 apud SATO, 2004: p. 32]. É muito importante que a turma já tenha trabalhado os conceitos supracitados.
Pedir para a turma trazer uma folha de papel-manteiga e proceder da seguinte forma:
- Trace uma reta diretriz d.
- Marque um ponto F fora dessa reta, o mesmo será o foco da parábola;
- Tome um ponto P` da reta d;
- Trace uma reta perpendicular r, à reta diretriz passando pelo ponto P`;
- Dobre a folha fazendo sobrepor o ponto P` ao ponto F (foco);
- Trace uma reta t coincidindo com a dobra feita;
- Marque o ponto de interseção de t com r;
- Repita o processo, tomando outros pontos sobre a reta d;
- Ligue os pontos de interseção das dobras com as perpendiculares que passam pelos pontos considerados sobre a reta d;
Figura 1: Construção a parábola através do método da dobradura
Fonte: http://www.mat.uel.br/matessencial/superior/pde/mirtes-parabolas-curvas-preciosas.pdf
Atividade 2: Construção de um refletor de raios luminosos
A turma, após terminar a construção através de dobradura, continuará em sala de aula e nos mesmos grupos, receberá orientações para a contrução de um refletor de raios luminosos, cuja seção transversal tem o formato de uma parábola. Tomando apenas esta seção, enfatize o fato de que os raios de luz irão incidir paralelamente ao eixo de simetria desta, comprovando uma das propriedades das parábolas que são utilizadas nas antenas parabólicas. Esta atividade foi retirada de [MACH 2007]. Incentive a turma a descobrir tal propriedade.
Figura 2: Refletores construídos [MACH, 2007]
Fonte: http://www.mat.uel.br/matessencial/superior/pde/mirtes-parabolas-curvas-preciosas.pdf
Para realizar esta construção acesse o link abaixo:
Disponível: http://www.mat.uel.br/matessencial/superior/pde/mirtes-atividade1-proposta.pdf
Acesso: 12/09/2010
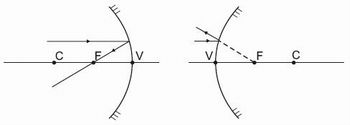
Professor, estabeleça previamente um planejamento com a equipe de Física da sua escola para trabalharem em parceria, onde seja proposto um trabalho em grupo, relacionando o conteúdo matemático com o conteúdo de Física, em Óptica, ao se trabalhar com a incidência de raios e propriedades de espelhos esféricos.
Figura 3: Propriedades de espelhos esféricos
Fonte: http://75.125.35.18/~moatha/farroupilha/downloads/optica-3.pdf
Atividade 3: Estratégias para a obtenção do vértice da função quadrática
Professor, a turma fará este desenvolvimento no caderno, em sala. Resgate o procedimento para a obtenção do vértice da parábola através da forma canônica, porém agora peça para a turma executar o processo descrito. Assim, temos que o xv pode ser obtido:
- calculando o ponto médio das raízes, isto é, se considerarmos m e n como raízes teremos que xv=(m+n)/2;
- observando que as translações horizontais e verticais tomando a função x2 como ponto de partida, são de –b/(2a) para a abscissa que é o xv e de f(-b/(2a)) para o yv do vértice, respectivamente, temos
Figura 4: Dedução da ordenada do vértice - Imagem da autora
Ressalte o fato de que b2-4ac também pode ser representado pela letra grega delta e chamado de discriminante.
Encaminhe sua turma para o laboratório de informática, pois para a execução das atividades 4, 5 e 6 é necessário ter recursos que viabilizem a exibição das atividades, tais como a projeção através de data show e a utilização dos computadores. Este último é de grande importância pois permite que os alunos assumam uma postura investigativa diante dos desafios propostos.
Professor, nesta aula você poderá utilizar outra ferramenta para facilitar o entendimento da sua turma, trata-se do software Nippe Descartes, cujas atividades propostas promovem a interação com o objeto de estudo.
Atividade 4: Máximo ou mínimo da parábola
Neste momento a turma deve concluir que o objetivo deste problema é encontrar a ordenada do ponto de máximo, ou seja, a ordenada do vértice (yv).
O desenvolvimento a seguir foi adaptado de um artigo disponível em :
http://portal.mec.gov.br/seb/arquivos/pdf/EnsMed/expensmat_icap3.pdf
Acesso: 31/08/10
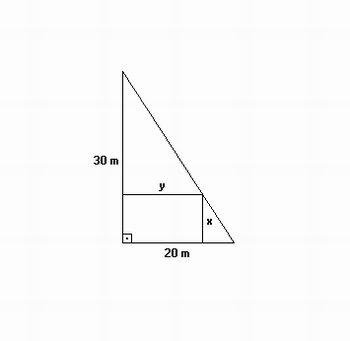
(Fuvest – 1992) Num terreno, na forma de um triângulo retângulo com catetos com medidas 20 e 30 metros, deseja-se construir uma casa retangular de dimensões x e y, como indicado na figura abaixo.
Figura 5: O problema do retângulo inscrito
Fonte: http://portal.mec.gov.br/seb/arquivos/pdf/EnsMed/expensmat_icap3.pdf
a) Exprima y em função de x.
b) Para que valores de x e de y a área ocupada pela casa será máxima?
Comentário: Logo, o vértice não será superado por nenhum outro ponto da parábola e, por este motivo será chamado de ponto de máximo. O y do vértice recebe neste caso o nome de valor máximo. Assim, a ordenada do vértice da parábola pode ter seu valor máximo ou mínimo quando estudamos as funções quadráticas com domínio no eixo horizontal (x).
a) A solução desta atividade pode ser encontrada utilizando a semelhança de triângulos, daí:
Figura 6: Semelhança - Imagem da autora
b) A área da casa á retangular, logo, temos que a mesma é dada por: A = x . y. Porém, como y é dado em função de x, segue:
Figura 7: Modelagem da função quadrática - Imagem da autora
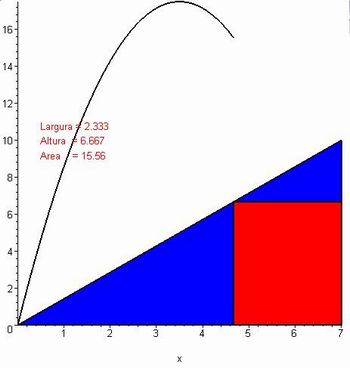
Como o sinal de a= - 2/3 é negativo, temos que a concavidade é voltada para baixo. Uma vez que estamos procurando o ponto cuja área é máxima, precisamos encontrar as coordenadas do vértice. Sendo as raízes 0 e 30, a abscissa do vértice, dada pelo ponto médio destas raízes é 15 e o valor da ordenada correspondente é 10.
Concluímos que a altura e a base do retângulo inscrito de área máxima são a metade, respectivamente, da altura e da base do triângulo.
A solução deste problema também pode ser obtida através de dobradura. Para análise do encaminhamento desta solução, visite o site http://portal.mec.gov.br/seb/arquivos/pdf/EnsMed/expensmat_icap3.pdf.
É importante que os alunos visualizem esta animação após a realização da atividade proposta para a turma observar a conexão entre a área do triângulo e a modelagem de uma função quadrática.
Disponível: http://portaldoprofessor.mec.gov.br/fichaTecnica.html?id=19061
Acesso: 30/08/10
Figura 8: Problema do retângulo inscrito - Imagem da Autora
Atividade 5: Relacionando o delta com o número de raízes
Para realizar esta atividade acesse:http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/FQuadr4.html
a) Calcule o valor de delta de cada uma das funções dadas abaixo.
i) y= (x-4)2 + 2 ii) y=2x2 – 2 iii) y=(x-4)2
iv) y= - (x+3)2 - 1 v) y=(-1/4)(x-1)2 + 1 vi) y= - 4x2
b) Obtenha as raízes destas funções.
c) Represente tais funções no plano cartesiano dado variando os valores de a, m, n e k.
d) O que você pode observar sobre o sinal do delta e o número de raízes?
a) i) delta = -56 ii) delta = 16 iii) delta = 0 iv) delta = -4 v) delta = 1 vi) delta = 0
b) Chamando as raízes de x1 e x2, temos:
i) Esta função não admite raízes, pois não intercepta o eixo x.
ii) As raízes são x1= -1 e x2=1
iii) As raízes são x1=x2=2
iv) Esta função não admite raízes, pois não intercepta o eixo x.
v) As raízes são x1= -1 e x2=3
vi) As raízes são x1=x2=0
Atividade 6: Estudando o sinal da função
Nesta etapa a turma utilizará as informações trabalhadas no momento anterior como base para as conclusões sobre o sinal da função.
Para realizar esta atividade acesse:http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/FQuadr5.html
a) Represente as funções abaixo no plano cartesiano dado variando os valores de a, m, n e k.
i) y= (x-4)2 + 2 ii) y=2x2 – 2 iii) y=(x-4)2 iv) y= - (x+3)2 - 1 v) y=(-1/4)(x-1)2 + 1 vi) y= - 4x2
b) Para cada item, observe no gráfico correspondente os valores de x para os quais: 1) y<0 2). y=0 3). y>0.
Comentário: Enfatize a discussão com a turma para a resolução de cada um dos itens.
A atividade a seguir pode assumir o papel de um desafio ou ainda uma avaliação.
Professor, previamente acesse o link:http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/ExerAula5.pdf .
Tire cópias e distribua para os alunos que estarão em sala de aula.
Atividade 7: Resolução e correção de exercícios
Solicite que os alunos retornem a sala de aula, ocupem seus lugares e a seguir distribua a atividade.
Informe aos alunos que esta atividade tem como objetivos a solidificação do conteúdo abordado.
Figura 9: Imagem da Autora
Permita que eles façam descobertas e respondam aos questionamentos por um tempo aproximado de 15 minutos. Peça, então, que os alunos relatem as suas descobertas e desenvolva no quadro com a participação da turma as soluções encontradas.
Recursos Complementares
Recursos Educacionais
| Nome |
Tipo |
| Visualização de Mathlets gerados pelo software Nippe Descartes |
Software Educacional - Animação |
Recursos Complementares
Software Nippe Descartes
O grupo de pesquisa “Tecnologias no Ensino da Matemática”, vinculado ao Projeto Fundão1, confeccionou diversas atividades utilizando o software Nippe Descartes, um aplicativo desenvolvido em Java que permite uma manipulação ágil e simples de janelas gráficas aplicáveis a qualquer página web. Este grupo reúne-se semanalmente e se propõe a desenvolver aplicações específicas para apresentação de conteúdos do Ensino Médio.
Página do Projeto Fundão: http://www.projetofundao.ufrj.br/matematica/
Para visualizar as atividades o professor deve:
1. Baixar o software Java disponível em: http://www.java.com/pt_BR/download/
2. Baixar o arquivo contendo as atividades.
Site consultado:
- Centro de referência virtual do professor http://crv.educacao.mg.gov.br/sistema_crv/index.asp?id_projeto=27&ID_OBJETO=105673&tipo=ob&cp=B53C97&cb=&n1=&n2=M%F3dulos%20Did%E1ticos&n3=Ensino%20M%E9dio&n4=Matem%E1tica&b=s
Referência Bibliográfica:
[MACH, 2007] MACHADO, Mirtes Tamy Gomes, Parábolas – As curvas preciosas, Programa de desenvolvimento educacional do Pará - 2007.
Disponível : http://www.mat.uel.br/matessencial/superior/pde/mirtes-parabolas-curvas-preciosas.pdf
Veja também as seguintes aulas que complementam este assunto:
- A Geometria na Construção do Conceito de Função Linear
- Telefonia Celular:- Qual operadora escolher? Um Problema para ser Resolvido com a Função Afim
- Procurando uma Estratégia para não Sair no Prejuízo: Estudo de Inequações do 1º grau
- Função Quadrática e suas Aplicações
- Inequações do Segundo Grau e suas Aplicações Práticas
Avaliação
Aplicação de atividades que abordem o tema para a fixação dos conteúdos apresentados. Tal avaliação deve ser feita ao observar as dúvidas dos alunos durante a realização das atividades sugeridas acima onde o professor terá a oportunidade de verificar o nível de entendimento ao circular pelos grupos durante o exercício 1 e também verificar se o processo de construção de gráficos foi apreendido do exercício 2.
Quatro estrelas 2 classificações
- Cinco estrelas 1/2 - 50%
- Quatro estrelas 1/2 - 50%
- Três estrelas 0/2 - 0%
- Duas estrelas 0/2 - 0%
- Uma estrela 0/2 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Serafim, Unisnatos , São Paulo - disse:
serafim@gmail.com.br26/03/2015
Cinco estrelasmuito boa
-
ALDEIR JOSE MOURA DA SILVA, Universidade Potiguar , Rio Grande do Norte - disse:
aldeirj@hotmail.com14/12/2014
Quatro estrelasMuito bom!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus