24/11/2010
Edson Luis Nunes, José Marcelo Gomes, Daniel Rodrigues Ventura.
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Física | Movimento, variações e conservações |
| Educação de Jovens e Adultos - 2º ciclo | Ciências Naturais | Visões de mundo |
O que o aluno poderá aprender com esta aula
· Determinar a velocidade de um satélite em órbita conhecendo sua altura.
· Calcular a velocidade que deve alcançar um satélite para que fique em órbita, a uma determinada altura, ao redor da Terra.
· Calcular a altura de um satélite estacionário a partir da massa e raio da Terra.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Movimento Circular Uniforme, Leis de Newton, Gravitação Universal.
Estratégias e recursos da aula
Sugerimos que o professor inicialmente assista ao vídeo histórico sobre o lançamento do SPUTNIK em 04 de outubro de 1957 pela União Soviética, se possível apresente o vídeo para os alunos e comente sobre a importância deste feito. Esse vídeo pode ser acessado no seguinte endereço:
http://www.youtube.com/watch?v=0_nUX61x3Cc&feature=related
Depois o professor poderá acessar e apresentar para os alunos, um texto com animações, bastante interessante e instrutivo, que mostra os tipos de órbitas dos satélites que traficam ao redor da Terra, e como cada órbita está relacionada com as finalidades que se deseja do satélite. Este texto pode ser acessado no endereço abaixo.
http://geocities.ws/redescefetpi/feitos/satelites/orbita.html
O professor ainda poderá mostrar a Figura 01 que ilustra o lixo deixado no espaço ao redor da Terra. Segundo a Agência Espacial Européia depois do lançamento do Sputnik já teriam sido lançado cerca de 6 mil satélites. Destes, apenas 800 estariam ativos e 45% estariam numa altura de até 32 mil km de altura. Além disso, as diversas naves espaciais ao serem enviadas ao espaço soltam alguns pedaços no céu aumentando ainda mais a sujeira no espaço próximo de nosso Planeta.
http://acertodecontas.blog.br/wp-content/uploads/2008/04/terra-lixo.thumbnail.jpg
Para se colocar um satélite em órbita, ele é levado por meio de foguetes, até a altura desejada, normalmente acima de 150 km para que forças de resistências não perturbe o seu movimento. Ao atingir a altura desejada o satélite então é lançado horizontalmente, também por meio de foguetes, com uma velocidade determinada para permanecer na sua órbita.
Atividade I
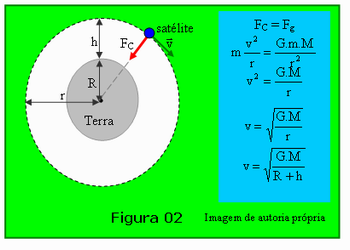
Depois o professor deverá mostrar a Figura 02 que esquematiza o movimento de um satélite em órbita circular ao redor da Terra. Após o satélite ser lançado, a única força que atuará nele será seu peso, isto é a força que a Terra o atrai. Como esta aponta para o centro da Terra, será perpendicular à sua velocidade, o que corresponde a força centrípeta. Portanto a força centrípeta do satélite é igual à força de atração da Terra sobre ele e esta é a única força no satélite.
Ao passar essas informações para a turma, peça a eles para determinar o valor da velocidade “v” do satélite em função da massa da Terra “M”, do raio da Terra “R” e da altura “h” que ele se encontra em órbita.
Para resolver o problema, observando na Figura 02 que o raio da órbita do satélite é r e que r = R + h. Depois considerar que o satélite se encontra em MCU, portanto a força resultante sobre ele é a força centrípeta FC que é devido a força de atração gravitacional da Terra sobre o satélite. Essa força é Fg = G.m.M/r2, G é a constante gravitacional universal e m a massa do satélite. Como a única força que atua no satélite é seu peso, força de atração gravitacional tem-se que ela equivale à força centrípeta, FC = Fg como no quadro à direita na Figura 02. Veja a resolução nesse quadro.
Atividade II
Depois o professor deverá explicar que um satélite geoestacionário é um satélite que se encontra fixo em relação à Terra, portanto sua órbita coincide com o plano equatorial e seu período com o período de rotação da Terra. Com essas considerações forneça os valores da Constante Gravitacional Universal G = 6,67.10-11 N.m/kg, a massa da Terra M = 5,98.1024 kg e o raio da Terra R = 6,37.106 m.
A partir dos valores informados, peça aos alunos que calculem a altura h a partir da superfície da Terra se deve encontrar um satélite estacionário. Como o exercício envolve muitos cálculos para agilizar o professor deverá permitir aos alunos que use calculadora.
Solução:
- Tomando como base o que foi dito no texto acima, tem-se que no satélite a única força que nele atua é a força gravitacional. Tomando como base que FC = Fg, segue desenvolvimento no quadro abaixo.
Depois substituindo na penúltima expressão os respectivos valores das grandezas envolvidas resulta na seguinte igualdade:
· 4.9,8696.r3 = (86400)2.6,67.10-11.5,98.1024
· 39,4784. r3 = 2,9775.1024
· r3 = 7,542.1022
· r3 = 75,42.1021
· r = 4,225.107 m
· r = 42,25.106 m
· Mas, como R + h = r, então h = r – R;
· h = 42,25.106 – 6,37.106
· h = 35,88.106 m
h = 35880 km, que é aproximadamente a altura de um satélite geoestacionário.
Atividade III
Após a correção do exercício anterior o professor poderá propor o seguinte exercício para que os alunos possam aplicar a teoria explicada.
Suponha que um determinado satélite se encontra em órbita circular ao redor da Terra e seu período seja de 3,0 horas. Considerando o raio da órbita de um satélite geoestacionário igual a 42000 km, determine a altura que se deve encontrar esse satélite.
Para resolver este exercício terão que utilizar uma relação que contempla as duas grandezas, período e raio altura dos satélites. Ou indiretamente, que é mais simples, considerando a relação entre os períodos e ao invés de altura diretamente, calcula-se primeiro o raio da órbita, como segue no quadro abaixo. O quadro fornece a resolução do exercício, obtendo uma altura de 4130 km para o hipotético referido satélite.
Recursos Complementares
Sugerimos que o professor assista ao vídeo sobre lançamento da Apollo 11 e se possível mostrar este vídeo aos alunos. Ele é interessante porque mostra o lançamento e acompanha durante o lançamento após contagem regressiva até cerca de 3 minutos indicando a cada segundo o valor da altura alcançada pelo foguete e sua velocidade naquele momento, inclusive mostra o momento em o foguete abandona seu primeiro estágio. Vale a pena conferir, o endereço eletrônico para acessar o vídeo como o respectivo título segue abaixo.
Apollo 11 launch w/ altitude and velocity data
Avaliação
Com objetivo de despertar mais interesse pelo assunto, sugerimos que o professor peça aos alunos para fazerem uma pesquisa sobre plataforma espacial e o que os programas espaciais podem vir a contribuir no futuro.
Sem estrelas 0 classificações
- Cinco estrelas 0/0 - 0%
- Quatro estrelas 0/0 - 0%
- Três estrelas 0/0 - 0%
- Duas estrelas 0/0 - 0%
- Uma estrela 0/0 - 0%
Denuncie opiniões ou materiais indevidos!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus