30/11/2010
Edson Luis Nunes, José Marcelo Gomes, Daniel Rodrigues Ventura.
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Física | Movimento, variações e conservações |
| Educação de Jovens e Adultos - 2º ciclo | Ciências Naturais | Visões de mundo |
O que o aluno poderá aprender com esta aula
· Conceituar trabalho de uma força.
· Determinar o trabalho realizado pela força elástica.
· Avaliar o trabalho realizado por uma força através de um gráfico.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Leis de Newton, Vetores.
Estratégias e recursos da aula
http://eternocondutor.sathyasai.org.br/Jul09/images/Img-07.jpg
Sugerimos que antes de iniciar sua aula, o professor use a Figura 01, que ilustra um homem aparentemente em seu escritório assentado ao lado da mesa, enquanto um garoto está brincando com um aviãozinho de papel. Mostre a gravura para os alunos e pergunte para eles:
Aquelas pessoas estão realizando algum trabalho ou quem está fazendo algum trabalho? Sobre o ponto de vista unicamente da Física no instante representado na figura, as pessoas estão desenvolvendo trabalho ou qual delas está realizando trabalho? Ou podemos afirmar que nenhuma delas está exercendo trabalho de acordo com o conceito de trabalho em Física?
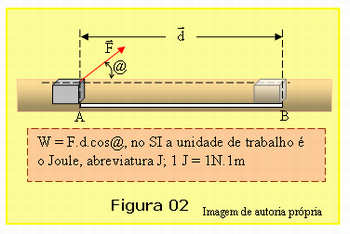
Após analisar as respostas, o professor deverá explicar para a turma o conceito de trabalho de uma força segundo a Física. Para isso pode utilizar a Figura 02 ou fazer um esquema semelhante para auxiliar sua explicação.
Quando uma força constante atua num objeto enquanto este se desloca, se o ângulo entre a direção da força e a direção do deslocamento mantiver sempre o mesmo valor, define-se o trabalho da força F sobre o objeto matematicamente por; W = FDcos(@), em que W é o trabalho realizado pela força, F é a força aplicada, d é o deslocamento do corpo enquanto a força atua e @ é o ângulo entre direção da força e do deslocamento. A unidade de trabalho no Sistema Internacional é o Joule, cuja abreviatura é J. O Joule é o trabalho realizado por uma força de 1 Newton atuando na direção e sentido do deslocamento do corpo quando este se desloca de 1 metro.
Atividade I
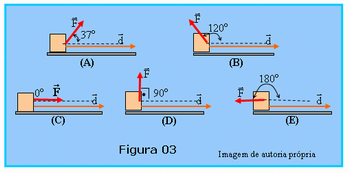
O professor após explicar o conceito de trabalho de uma força constante deverá usar a Figura 03 que ilustra cinco esquemas (A), (B), (C), (D) e (E). Em cada esquema um bloco se desloca horizontalmente de uma distância d enquanto nele atua uma força F cuja direção em relação à d, varia em cada caso.
O professor deverá pedir à turma que nos esquemas da Figura 03, faça F = 10 N, d = 1,0 m e calcule o valor do trabalho W em cada caso.
Deverão encontrar, usando a fórmula de trabalho de uma força, W = F.d.cos@, @ ângulo entre F e d, valor de @ indicado em cada esquema.
Esquema A (@ = 37 graus), cos37 = 0,80.
· W = 10N.1,0m.0,80
· W = 8,0 J
Esquema B (@ = 120 graus), cos120 = -0,87.
· W = 10N.1,0m.(-0,87)
· W = -8,7 J
Esquema C: (@ = 0 grau), cos0 = 1,0.
· W = 10N.1,0m.1,0
· W = 10 J
Esquema D: (@ = 90 graus), cos90 = 0.
· W = 10N.1,0m.(0)
· W = 0
Esquema E: @ = 180 graus), cos180 = -1,0.
· W = 10N.1,0m.(-1,0)
· W = -10 J
Ao resolver o problema acima, o professor então deverá chamar a atenção para os casos particulares ilustrados em cada esquema da Figura 03.
1. No esquema A da figura, o ângulo formado entre a força F e a direção do deslocamento d é um ângulo agudo. Neste caso o trabalho realizado pela força é positivo, quando o trabalho realizado pela força é positivo, denomina-se trabalho mecânico.
2. No esquema B, o ângulo formado entre a força F e a direção do deslocamento d é um ângulo obtuso, entre 90 e 180 graus. Neste caso o trabalho realizado pela força é negativo, quando o trabalho realizado pela força é negativo, denomina-se trabalho resistivo.
3. No esquema C, o ângulo formado entre a força F e a direção do deslocamento d é igual à zero, ou seja, F e d têm mesma direção e mesmo sentido. Neste caso o trabalho realizado pela força é igual ao produto da força pelo deslocamento, W = F.d, o trabalho é positivo, trabalho mecânico.
4. No esquema D, o ângulo formado entre a força F e a direção do deslocamento d é um ângulo reto, 90 graus. Neste caso o trabalho é nulo, pois cos90 é nulo. É um caso particular em que a força não realiza trabalho.
5. No esquema E, o ângulo formado entre a força F e a direção do deslocamento d é um ângulo raso, 180 graus. Neste caso o trabalho realizado pela força é igual ao produto de F e d, porém negativo. W = -F.d, trabalho resistivo.
Atividade II
O professor então deverá explicar que na maioria das vezes que uma força executa um trabalho, seu valor não é constante. Neste caso não é aplicável a fórmula anterior, mas se dispusermos de um gráfico que indica como o valor da força ou de sua componente paralela ao deslocamento varia ao longo do deslocamento, podemos determinar o trabalho por ela realizado, através da área entre a curva representativa e o eixo das abscissas, no gráfico.
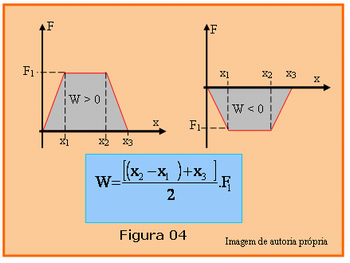
Para facilitar sua explicação ele poderá usar a Figura 04 que corresponde a dois gráficos indicando como o valor de uma força F que atua num corpo qualquer varia em função do deslocamento x. Deve-se salientar que a força F e x, representados no gráfico, possui mesma direção. A área cinza nos gráficos corresponde ao trabalho W exercido pela força F durante o deslocamento x correspondente. No gráfico A, o trabalho é positivo, a força tem mesmo sentido do deslocamento e no gráfico B, o trabalho é negativo, neste caso a força tem sentido contrário ao deslocamento, observe no gráfico que seu sinal é negativo. Na Figura 04 também está indicada a expressão para calcular a área nos dois gráficos, área do trapézio.
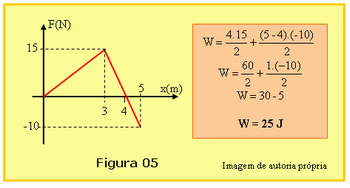
Em seguida o professor poderá usar o gráfico da Figura 05 que fornece a variação da força F em função do deslocamento d, durante um deslocamento de 5,0 m. Sendo a Força paralela ao deslocamento no percurso durante o movimento do corpo, peça para os alunos calcularem o trabalho realizado pela força nesses 5,0 metros. A área entre a representação gráfica e o eixo das abscissas corresponde à área de dois triângulos cujas áreas como sabemos é o semi-produto da base pela altura. O primeiro triângulo, de zero a 4 metros, tem base igual a 4 m e altura igual a 15 N; o outro triângulo de 4 a 5m tem base de 1 m e altura é negativa de (-10) m. O exercício está resolvido no quadro á direita na Figura 05.
Atividade III
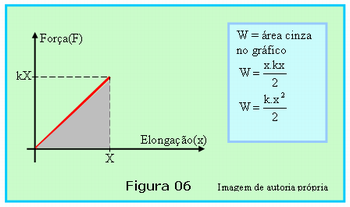
A Figura 06, abaixo, representa o gráfico da F para esticar uma mola de constante elástica k em função da deformação x por ela sofrida.
Oculte o quadro à direita da figura e mostre o gráfico para os alunos, ou então trace o gráfico no quadro da sala de aulas e peça para a turma calcular o trabalho realizado pela força em função da constante elástica k e da deformação X.
A resolução está no quadro à direita da Figura 06.
Agora atribua valores de k igual a 1000 N/m e X igual a 10 cm e peça que calculem o módulo do trabalho realizado pela força elástica da mola, lembrando que a força elástica tem sentido contrário ao deslocamento da mola, portanto o trabalho da mola é resistivo.
Usando a expressão da figura vão encontrar que:
· W = k.X2/2; X = 10 cm = 0,10 m
· W = 1000.(0,10)2/2
· W = 500.0,010 (Unidades do SI)
· W = 5,0 J
Para fechar o conteúdo da aula, o professor poderá elaborar um exercício com a finalidade de revisar as instruções fornecidas durante a aula. Sugerimos o seguinte problema.
Um cilindro de 50 kg é rolado subindo uma rampa de 30 graus de inclinação em relação a horizontal e 20 m de comprimento até atingir o topo, depois o cilindro rola outra rampa para baixo de comprimento também de 20 m, porém inclinada de 53 graus em relação à horizontal. Faça o esquema que representa o movimento e calcule o trabalho efetuado pelo peso do cilindro durante todo o movimento. g = 10 m/s2.
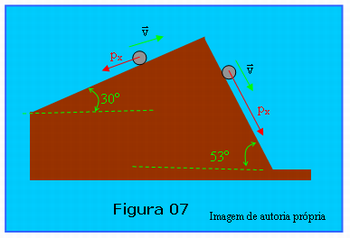
Para explicar a resolução do exercício poderá seguir o esquema representado na Figura 07. Durante a subida a componente do peso paralela à rampa tem sentido contrário à velocidade v, sentido que o corpo se move, portanto o trabalho é negativo; depois na descida, segunda rampa, o sentido da componente do peso paralela à superfície da rampa tem sentido coincidente com o sentido do movimento, neste trecho o trabalho é positivo.
A Figura 07 esquematiza o movimento do cilindro indicando por meio de vetores, a componente de seu peso paralela à rampa e a velocidade do mesmo. Durante a subida, a componente do peso paralela à rampa tem sentido para baixo, ou seja, contrário ao sentido do movimento, portanto na primeira rampa o trabalho é negativo e vale: W1 = -p.sen30.d1. Na descida a componente do peso do cilindro paralela à superfície da rampa tem mesmo sentido de v, mesmo sentido do movimento, portanto o trabalho do peso na segunda rampa é positivo, cujo valor é: W2 = p.sen53.d2. O trabalho total será:
· W = W1 + W2.
· W = -p.sen30o.20 + p.sen53o.20
· W = -m.g.0,50.20 + m.g.0,80.20
· W = -50.10.0,50.20 + 50.10.0,80.20 (em unidades do SI)
· W = -5000 + 8000
· W = 3000
· W = 3,0.103 J
Recursos Complementares
Sugerimos ao professor que assista ao vídeo sobre definição de trabalho de uma força e se possível apresente esse vídeo na sala de aula para os alunos, é bem ilustrativo e didático. Esse vídeo se encontra disponível com o título e endereço a seguir:
Novo Telecurso - Ensino Médio - Física - Aula 14 (1 de 2): 8 min e 6s
Avaliação
Os exercícios desenvolvidos durante a aula já são suficientes para verificação do aprendizado durante a aula, mas o professor ainda poderá elabora outros exercícios deste assunto, como abaixo.
A superfície de um plano inclinado tem comprimento d e altura h. Mostre que o trabalho do peso de um objeto ao descer um plano desde o topo até a parte mais baixa é mgh.
Três estrelas 3 classificações
- Cinco estrelas 1/3 - 33.33%
- Quatro estrelas 1/3 - 33.33%
- Três estrelas 0/3 - 0%
- Duas estrelas 1/3 - 33.33%
- Uma estrela 0/3 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Gildenclecio, Centro Educacional Antônio Honorato. , Bahia - disse:
aliasextra@outlook.com24/06/2014
Quatro estrelasMuito bom, espero que eu consiga usar quando for necessário.
-
Hebe, Oi , São Paulo - disse:
camargohebe@yahoo.com.br29/08/2013
Duas estrelasAchei meio complicado de entender.
-
ELIANE, UNIPAMPA SAO GABRIEL-RS , Rio Grande do Sul - disse:
lita.mota@yahoo.com.br13/02/2013
Cinco estrelasObrigada!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus