30/11/2010
Edson Luis Nunes, José Marcelo Gomes, Daniel Rodrigues Ventura.
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Educação de Jovens e Adultos - 2º ciclo | Ciências Naturais | Visões de mundo |
| Ensino Médio | Física | Movimento, variações e conservações |
O que o aluno poderá aprender com esta aula
· Analisar a situação de equilíbrio de uma partícula.
· Determinar a condição de equilíbrio de uma partícula.
· Resolver problemas envolvendo equilíbrio de partículas.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Leis de Newton, Vetores, soma e decomposição de vetores.
Estratégias e recursos da aula
Sugerimos que inicialmente o professor comente com os alunos sobre o conceito de partícula, em Física.
O termo partícula deriva do latim que significa parte muito pequena, é uma quantidade de matéria que se supõe ocupar um único ponto no espaço. Em Física é comum considerar um corpo como uma partícula, quando este tem dimensões desprezíveis em relação ao sistema em que se encontra, por exemplo, um ônibus percorrendo a estrada do Rio de Janeiro a Belo Horizonte, as dimensões do ônibus podem ser desprezadas em função da distância entre as duas cidades passando a ser considerado um ponto móvel; ou quando seu comportamento pode ser reduzido ao comportamento de uma partícula, por exemplo, uma bola pendurada no teto de uma sala por meio de um barbante.
Depois o professor poderá falar sobre situação de equilíbrio: se uma partícula estiver em equilíbrio, ela estará forçosamente em repouso ou se movendo em linha reta com velocidade constante, isto é, em MRU.
A condição para que uma partícula se encontra em equilíbrio, segundo a primeira e segunda lei de Newton é que a soma das forças que atuam nela, força resultante, seja nula.
Resumindo: Situação de equilíbrio de uma partícula: Repouso ou MRU. Condição de equilíbrio de uma partícula: soma das forças que nela atuam é igual a zero.
Em um corpo extenso, se as linhas de ação de todas as forças que nele atuam concorrem em um único ponto, aplica-se essa mesma condição de equilíbrio, é como se todas as forças fossem aplicadas no ponto de intersecção das linhas de ação. Sendo nula a resultante dessas forças, o corpo estará em equilíbrio. Linha de ação de uma força é a reta que contém a força.
Atividade I
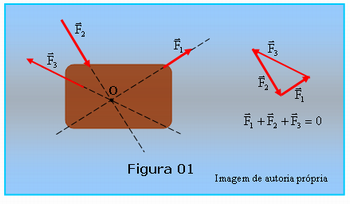
Após essas informações apresente a Figura 01 para a turma. Nessa figura há um esquema de forças coplanares atuando em um corpo extenso. Essas forças concorrem em um único ponto, ponto “O” no esquema. Como a soma dessas forças se anula, veja à esquerda na figura que a soma das três forças pelo método do polígono forma um triângulo, logo a resultante é nula, conclui-se que o corpo se encontra em equilíbrio.
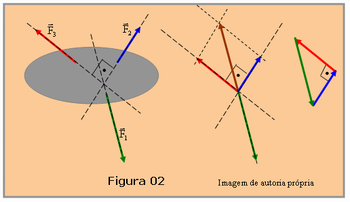
Agora observe a Figura 02 que corresponde ao esquema de três forças atuando numa prancha e considere que estas forças tenham módulos de: F2 = 18 N, F3 = 24 N e F1 = 30 N. Se a soma de três forças é igual a zero, é necessário e suficiente que uma delas seja igual e oposta a soma das outras duas. Apresente o esquema à esquerda na Figura 02 e peça aos alunos que usando as instruções deste parágrafo faça o seguinte:
· Determinar geometricamente a soma das forças F2 e F3 usando a regra do paralelogramo. Compare a resultante obtida com a força F1. “A escolha de F2 e F3 é porque elas formam entre si um ângulo reto, facilitando o resultado minimizando erros ao desenhar”.
· Calcule o módulo da força resultante da soma de F2 e F3 e compare com o módulo de F1.
· Com as respostas obtidas que conclusão pode ser tirada da soma das três forças atuantes na prancha?
· Qual deverá ser o estado de movimento da prancha?
· Se estiver em equilíbrio faça a soma geométrica usando o método do polígono, triangulação neste caso, e mostre como a resultante é nula.
A resolução geométrica da primeira parte do exercício está na Figura 02. Observa-se que a soma das forças F2 e F3 tem mesma direção e sentido oposto à força F1, e possui mesmo módulo, mesmo comprimento, que pode ser conferidos por meio de uma régua. Usando Pitágoras pode-se confirmar que o módulo de F1 equivale ao módulo da resultante R, soma vetorial, de F2 + F3. R = (F2)2 + (F3)2. R = (18)2 + (24)2; R = 324 + 576; R = 900; R = 30 N. Em que os destaques em negritos nas letras F se refere à grandezas vetoriais. A resultante de todas as forças que atuam na prancha é, portanto nula, o que implica em situação de equilíbrio. Ela estará em repouso ou em MRU. A triangulação das três forças está esquematizada à direita na Figura 02, como os vetores força se fecham em um triângulo, a soma das três é nula.
Atividade II
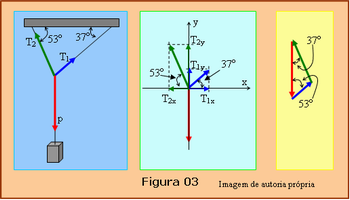
Depois mostre para a turma o quadro à esquerda na Figura 03. Nele há o esquema de um bloco de peso p, vetor em vermelho, pendurado no teto de uma sala por meio de fios inextensíveis. Os ângulos entre a direção de cada fio e a horizontal estão cotados neste esquema 37 e 53 graus respectivamente. As trações nos dois ramos do fio são T1, vetor em azul, e T2, vetor em verde.
Peça aos alunos que utilizando a condição de equilíbrio, calcule os valores das trações T1 e T2 em função de p. Dados para o problema: sen37 = cos53 = 0,6 e cos37 = sen53 = 0,8.
Solução:
Como as três forças se anulam, há pelo menos três maneiras de resolver este problema, como abaixo.
1. Considere o quadro do meio na Figura 03. Decompondo os vetores e usando a condição de equilíbrio de uma partícula, temos:
· Resultante das forças que atuam na partícula nula, isto e, soma das forças na direção x igual a zero e soma das forças na direção y igual a zero. Direção x:
· T1x – T2x = 0
· T1x = T2x
· T1.cos37 = T2..cos53
· T1.0,8 = T2.0,6
· T1 = 0,75T2 Na direção y:
· T1y + T2y – p = 0
· T1y + T2y = p
· T1.sen37 + T2.sen53 = p
· T1.0,6 + T2.0,8 = p
· T1 = 0,75.T2
· 0,75.0,6T2 + 0,8T2 = p
· 1,25.T1 = p
· T2 = p/1,25
· T2 = 0,8p
· T1 = 0,75T2
· T1 = 0,75.0,8p
· T2 = 0,6p
2. Considerando o esquema na direita da figura podemos usar a relação dos senos:
· T1/sen37= T2/sen53 = p/sen90
· T1/0,6 = p/1
· T1 = 0,6p
· T2/0,8 = p/1
· T2 = 0,8p
3. Usando as relações trigonométricas em um triângulo retângulo tem-se:
· Sen37 = T1/p
· T1 = sen37.p
· T1 = 0,6p
· Sen53 = T2/p
· T2 = sen53.p
· T2 = 0,8p
Atividade III
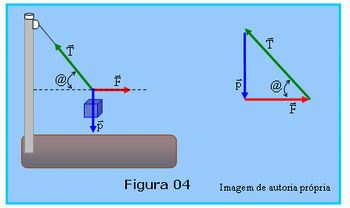
A Figura 04 ilustra um esquema em que um bloco está pendurado numa corda presa a um poste e uma outra corda puxada por uma força F, na direção horizontal. O bloco tem peso p e se encontra em equilíbrio na posição indicada pela figura.
Se o professor dispuser de dois dinamômetros poderá montar o esquema da figura, usando um objeto qualquer de peso conhecido. Os dinamômetros deverão ser presos, um na extremidade superior da corda ligando a corda ao ponto fixo no poste, e o outro no ponto de ação da força F, as leituras desses dinamômetros fornecerão os valores de T e F. Se fizer a montagem, peça aos alunos para medirem o ângulo @ e as respectivas leituras nos dinamômetros. Depois deverão mudar o ângulo @ e observar a alteração das leituras nos dinamômetros.
Independente que faça a montagem, peça aos alunos que considerem o peso do bloco igual a 1000 N, sen@ = 0,64, cos@ = 0,77 e com base no esquema da Figura 04 determine os valores de F e T, usando decomposição das forças nas direções horizontal e vertical e depois usando o esquema à direita.
Pela condição de equilíbrio:
Na horizontal,
· F – Tcos@ = 0
· F = Tcos@
Na vertical,
· Tsen@ - p = 0
· Tsen@ = p
· T.0,64 = 1000
· T = 1563 N
· F = Tcos@
· F = 562,5.0,77
· F = 1203 N
Pela relação no triângulo retângulo,
· sen@ = p/T
· T = p/sen@
· T = 1000/0,64
· T = 1563 N
· cos@ = F/T
· F = T.cos@
· F = 1563.0,77
· F = 1203 N
Recursos Complementares
Sugerimos que o professor acesse e assista ao seguinte vídeo que é uma animação sobre equilíbrio de partículas, com o título e endereço a seguir:
P.O.N.T.O.S: equilíbrio de partículas
http://portaldoprofessor.mec.gov.br/fichaTecnica.html?id=924
Avaliação
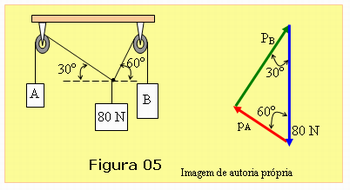
Peça aos alunos que utilizando o esquema da Figura 05 encontre os valores dos pesos pA e pB, dos blocos A e B, para que o sistema fique em equilíbrio na posição mostrada na figura. Dados para o problema: Sen30 = 0,50; sen60 = 0,87 e sen90 = 1,00.
Cinco estrelas 2 classificações
- Cinco estrelas 2/2 - 100%
- Quatro estrelas 0/2 - 0%
- Três estrelas 0/2 - 0%
- Duas estrelas 0/2 - 0%
- Uma estrela 0/2 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Pedrosa, Moriah , São Paulo - disse:
lontevar@uol.com.br08/09/2013
Cinco estrelasTrabalho muito bom!
-
Marcelo, Universidade Federal do Ceará , Ceará - disse:
fmarcelo92@gmail.com22/06/2013
Cinco estrelasConteúdo bem abrangente !
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus