14/01/2011
Clayton Gonçalves Silva, Fernando Celso Villar Marinho, Ivail Muniz Junior, Jackson Lopes, Raquel Cupolillo Simões de Sousa, Rita Maria Cardoso Meirelles
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Tecnologia para a matemática |
| Ensino Médio | Física | Movimento, variações e conservações |
| Ensino Médio | Matemática | Geometria |
O que o aluno poderá aprender com esta aula
Reconhecer o ciclo trigonométrico.
Identificar o seno e o cosseno no ciclo trigonométrico.
Determinar e relacionar os valores do seno e do cosseno dos ângulos de 0, 90, 180, 270 e 360 graus.
Relacionar valores mínimos e máximos, sinal e crescimento/decrescimento do seno e do cosseno.
Identificar a relação trigonométrica fundamental: sen2a + cos2a = 1
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Plano cartesiano
Comprimento da circunferência e de um arco contido na mesma
Medidas de arcos e ângulos em graus e em radianos
Razões trigonométricas no triângulo retângulo
Teorema de Pitágoras
Estratégias e recursos da aula
Professor, considerando que o aluno já aprendeu as razões trigonométricas no triângulo retângulo, inicie a aula recordando o significado da palavra trigonometria, como a seguir:
A palavra Trigonometria é formada por três radicais gregos: tri (três), gonos (ângulos) e metron (medir).
Conte então para os alunos sobre as primeiras aplicações clássicas da trigonometria. Você pode obter essas e outras informações adicionais, acessando o link: http://www.mat.ufrgs.br/~portosil/trigapl.html.
Fale ainda sobre a aplicação da trigonometria como um instrumento potente de cálculo, utilizado na Matemática e, também, em outras áreas, como no estudo de fenômenos físicos, eletricidade, mecânica, dinâmica, música, astronomia, topografia, engenharia entre outros.
O Ciclo Trigonométrico
Para introduzir o conceito de ciclo (círculo) trigonométrico mostre, primeiramente, uma aplicação no contexto da Física, que envolve movimento circular.
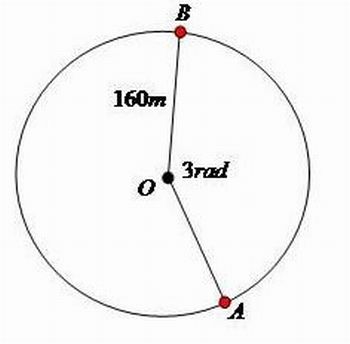
Com o auxílio do Data Show exiba a imagem abaixo e solicite que os alunos observem a figura para, em seguida, determinarem o intervalo de tempo que um móvel gasta para percorrer o arco de circunferência AB, cuja velocidade constante é de 24 m/s.
Nota: Espera-se que o aluno saiba que o intervalo de tempo corresponde à razão entre o espaço percorrido e a velocidade.
Fonte: http://www.brasilescola.com/matematica/arcos-movimento-circular.htm
1. Enfatizar que o percurso AB é feito no sentido anti-horário e que a medida do arco AB é igual ao ângulo central correspondente (3 rad).
2. Que a circunferência que contém o arco AB tem centro em O e raio igual a 160 m.
3. É preciso determinar o espaço percorrido (determinar o comprimento do arco AB).
Obs: Caso necessário, recorde aos alunos que o comprimento de um arco é igual ao produto das medidas do raio pelo arco (em radianos).
Ou seja: e = 160 m x 3 = 480 m
4. Calcular o intervalo de tempo: t = 480/24 = 20 segundos.
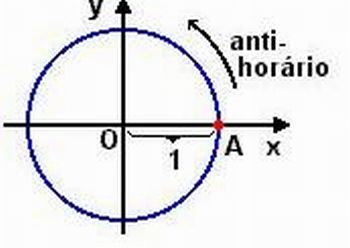
Nota: Antes de introduzir o conceito de ciclo trigonométrico, utilize o Data Show e exiba a imagem a seguir.
Fonte: http://pessoal.sercomtel.com.br/matematica/trigonom/trigo01.htm
Faça algumas considerações para a turma, tais como:
Consideremos uma circunferência no plano cartesiano. Se um ponto está localizado sobre a mesma, simplesmente dizemos que ele pertence à circunferência e que é um ponto fixo na mesma. Se assumirmos que este ponto possa ser deslocado sobre a curva, este ponto receberá o nome de ponto móvel.
Um ponto móvel localizado sobre uma circunferência, partindo de um ponto A pode percorrê-la em dois sentidos opostos. Por convenção, o sentido anti-horário (contrário aos ponteiros de um relógio) é adotado como sentido positivo.
Nota: Professor, como a atividade proposta a seguir, requer manipulação de medidas de ângulos em radianos, e se considerar necessário, faça uma breve revisão sobre o assunto. Você pode acessar o link: http://pessoal.sercomtel.com.br/matematica/trigonom/trigo01.htm e utilizá-lo como fonte de pesquisa.
Encaminhe a turma ao laboratório de informática e permita que os alunos se agrupem em, no máximo, três por computador, de forma a realizar as atividades a seguir.
Atividade 1:
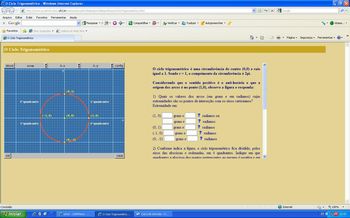
Peça que os alunos acessem o link: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/CicloTrigonometrico.html e iniciem a atividade que tem por objetivo, através da observação, permitir que o aluno reconheça o ciclo trigonométrico e identifique arcos compreendidos no mesmo.
Obs: Permita que a turma a manipule por um tempo de aproximadamente 15 minutos e, em seguida, confira as soluções encontradas, discutindo e elucidando possíveis erros cometidos pelos alunos.
Imagem do autor.
1, Arcos com extremidade no ponto
a) (1, 0): 0º, 0 rad (na origem) ou 360º; 2pi rad (uma volta completa)
b) (0, 1): 90º; pi/2 rad
c) (–1, 0): 180º; pi rad
d) (0, –1): 270º; 3pi/2 rad
2. Abscissas positivas: 1o e 4o quadrantes; abscissas negativas: 2o e 3o quadrantes
Ordenadas positivas: 1o e 2o quadrantes; ordenadas negativas: 3o e 4o quadrantes
3. a) 1o; b) 3o; c) 2o; d) 4o; e) 1o; f) 3o; g) 4o; h) 3o
Professor, antes de apresentar o seno e o cosseno no ciclo trigonométrico, é importante que os alunos revejam as razões trigonométricas no triângulo retângulo.
Sugerimos que essa revisão seja feita a partir do recurso do portal:
que simula as razões trigonométricas associadas a um triângulo retângulo. Solicite que os alunos a manipulem pelo tempo que achar conveniente.
Obs: Finalizada a revisão, é hora de a turma ser apresentada ao seno e ao cosseno no ciclo trigonométrico!
Nas atividades a seguir, o aluno é o foco da aprendizagem, com um papel extremamente ativo nesse processo. O dinamismo da interação do aluno com o programa pode ajudar muito na compreensão da trigonometria no ciclo unitário. É muito importante que o professor acompanhe atentamente a interação do aluno com os aplicativos e com os seus colegas de classe.
Atividade 2:
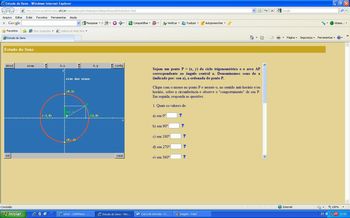
Para que os alunos observem, manipulem, analisem e tirem suas próprias conclusões sobre o “comportamento” do seno no ciclo, peça para acessarem o link: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/EstudoSeno.html e iniciarem a atividade.
Permita a manipulação da mesma por um tempo aproximado de 20 minutos para, em seguida, propiciar relatos das descobertas dos alunos e conferir as soluções encontradas pelos mesmos.
Imagem do autor.
1. a) sen 0º = 0; b) sen 90º = 1; c) sen 180º = 0; d) sen 270º = –1; e) sen 360º = 0
2. valor mínimo = –1 e valor máximo = 1
3. sen a > 0 para 0 < a < 180º
4. sen a < 0 para 180º < a < 360º
5. crescente: 1º e 4º quadrantes; decrescente: 2º e 3º quadrantes
Solicite que os alunos registrem em seus cadernos, um resumo com as descobertas feitas e as soluções encontradas.
Atividade 3:
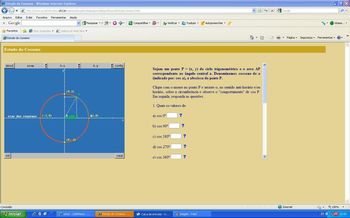
Peça para os alunos acessarem o link: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/EstudoCosseno.html e iniciarem a atividade que aborda o “comportamento” do cosseno no ciclo.
Assim como na atividade anterior, permita a manipulação da mesma por um tempo aproximado de 15 minutos para, em seguida, propiciar relatos das descobertas dos alunos e conferir as soluções encontradas pelos mesmos.
Imagem do autor.
1. a) cos 0º = 1; b) cos 90º = 0; c) cos 180º = –1; d) cos 270º = 0; e) cos 360º = 1
2. valor mínimo = –1 e valor máximo = 1
3. cos a > 0 para –90º < a < 90º
4. cos a < 0 para 90º < a < 270º
5. crescente: 3º e 4º quadrantes; decrescente: 1º e 2º quadrantes
Obs: Mais uma vez solicite que os alunos registrem em seus cadernos, um resumo com as descobertas feitas e as soluções encontradas.
Professor, explorando as atividades desenvolvidas pelos alunos, peça que apliquem o Teorema de Pitágoras no triângulo retângulo cujos catetos são sen a e cos a, e a hipotenusa é igual a 1, como a seguir:
(sen a)2 + (cos a)2 = 1
Ou seja: sen2a + cos2a = 1
Nota: Informe que essa é uma das relações trigonométricas fundamentais.
Ao final da aula espera-se que o aluno saiba aplicar os conhecimentos adquiridos em situações que envolvem seno e cosseno nas diversas áreas de estudo em que se aplicam tais conteúdos.
Recursos Educacionais
| Nome | Tipo |
|---|---|
| Definição das razões trigonométricas | Animação/simulação |
Recursos Complementares
Fontes de pesquisa:
http://educacao.uol.com.br/matematica/ult1705u41.jhtm
http://pt.wikipedia.org/wiki/Trigonometria#Seno
http://pt.wikipedia.org/wiki/Trigonometria#Cosseno
http://www.colegiocatanduvas.com.br/desgeo/trigonometira/index.htm
Projeto Fundão:
O grupo de pesquisa “Tecnologias no Ensino da Matemática”, confeccionou diversas atividades utilizando o software Nippe Descartes, um aplicativo desenvolvido em Java que permite uma manipulação ágil e simples de janelas gráficas aplicáveis a qualquer página web.
Para visualizar as atividades o professor deve:
1. Baixar o software Java disponível em: http://www.java.com/pt_BR/download/
2. Baixar o arquivo contendo as atividades.
Avaliação
Avaliar a participação dos alunos durante as atividades desenvolvidas.
Realização de um trabalho de pesquisa em que a turma, dividida em 5 grupos ou mais, conforme o número de alunos, deverá pesquisar temas interdisciplinares em que a trigonometria é aplicada.
— Determine um prazo para que a mesma seja feita e informe-os de que cada grupo deverá apresentar seu trabalho para o restante da turma, propiciando observações, análise e debate sobre o assunto abordado em cada trabalho.
Cinco estrelas 1 classificações
- Cinco estrelas 1/1 - 100%
- Quatro estrelas 0/1 - 0%
- Três estrelas 0/1 - 0%
- Duas estrelas 0/1 - 0%
- Uma estrela 0/1 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Claudecir, COLÉGIO DR. DORIVAL BRANDÃO DE ANDRADE , Goiás - disse:
claudecircoelho@yahoo.com.br13/03/2011
Cinco estrelasParabéns pelas atividades, realmente assim fica difícil não aprender trigonometria no círculo.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus