12/01/2011
Aparecida Clemilda Porto
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Fundamental Inicial | Matemática | Espaço e forma |
| Educação de Jovens e Adultos - 1º ciclo | Matemática | Geometria |
| Ensino Médio | Matemática | Geometria |
| Educação de Jovens e Adultos - 2º ciclo | Matemática | Grandezas e medidas |
O que o aluno poderá aprender com esta aula
- Classificar os poliedros em pirâmide ou prismas de acordo com suas características.
- Classificar os corpos redondos em esferas, cones e cilindros de acordo com suas características.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
1) Os alunos deverão ter conhecimento dos polígonos e suas características.
2) Saber distinguir corpos redondos de poliedros.
Estratégias e recursos da aula
1ª ATIVIDADE
Nesta atividade, os alunos deverão distinguir os diferentes corpos redondos e poliedros. Para isso, professor, oriente-os, previamente, para providenciar, para a aula seguinte, figuras ou objetos que tenham a forma de diferentes sólidos.
Obs.:
1) O trabalho deverá ser realizado em grupos de 5 alunos.
2) Para o caso de algum aluno não providenciar os objetos que representem algum sólido geométrico (cones, cilindros, prismas de bases diferentes, troncos de sólidos geométricos etc.), o professor dever ter o cuidado de providenciá-los, com antecedência, para serem usados na aula deste conteúdo.
PARTE I: CLASSIFICAÇÃO DOS CORPOS REDONDOS
I) CILINDRO
1) Os grupos deverão organizar os sólidos sobre a mesa do professor.
2) A seguir, o professor deverá pedir ao grupo que retire da mesa os objetos que não correspondem aos corpos redondos. Um aluno por vez deverá retirar um objeto, justificando sua escolha.
NOTA:
A justificativa deve ser aceita por todos do grupo, senão o professor deverá intervir para que cheguem a um acordo. A intervenção deve conter questões como:
“Quais objetos têm superfície esférica?”
“Quais desses corpos não rolam ou giram?”
Com essas perguntas, os alunos retomam o estudo anterior sobre a caracterização dos corpos redondos e dos poliedros.
1) O professor deve, então, entregar ao grupo uma ficha que contenha questões como as listadas a seguir:
(A) Separe as figuras que têm duas bases congruentes.
NOTA:
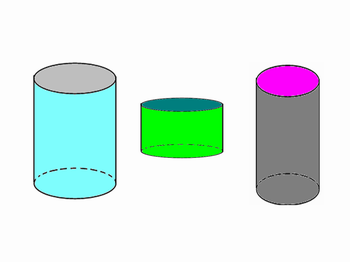
Nesse item, os alunos deverão separar os diversos objetos na forma de: latas, embalagens, etc. que se pareçam com as formas a seguir:
GRUPO DE CILINDROS
(B) Qual é a forma dessas bases?
NOTA:
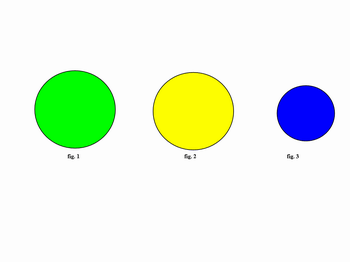
Ao verificar se as bases são círculos, o professor deve questionar se elas são congruentes, pedindo que justifiquem. Se o aluno tiver dúvida, o professor deve ter já pronto dois círculos que, quando sobrepostos, têm todos os pontos em comum. Assim, o aluno retoma a ideia de que duas figuras são congruentes quando possuem todas as medidas iguais. Ele pode mostrar também dois círculos não congruentes, conforme modelo a seguir.
Ao sobrepor a figura 1 com a figura 2, os alunos verão que são congruentes e, ao sobrepor a figura 1 ou figura 2 com a figura 3, eles observarão que não são.
(C) Elas têm a mesma forma? Se tiverem, em que se diferenciam?
NOTA:
Essa questão é para reforçar que todos os corpos redondos apresentados têm bases congruentes circulares, portanto, são parecidas. A diferença entre elas está apenas no tamanho das dimensões (comprimento, largura e altura).
(D) Como se chamam os corpos redondos que vocês separaram?
NOTA:
O professor deve apresentar essas figuras – sólido geométrico (corpo redondo) - que têm duas bases circulares paralelas e congruentes – nomeando-as como cilindros e, em seguida, pedir para que os grupos conceituem cilindros, representando-os por desenhos.
(E) Portanto, cilindro é: ............................................................................................................................................. ............................................................................................................................................. .............................................................................................................................................
II) CONE
1) O professor deve então entregar ao grupo uma ficha que contenha questões como as listadas a seguir:
(A) Separe as figuras que têm apenas uma base.
NOTA:
Nesse item, os alunos deverão separar os diversos objetos na forma de cones: chapéu, casquinha de sorvete (o professor deve providenciá-los com antecedência), latas, embalagens, etc.
NOTA:
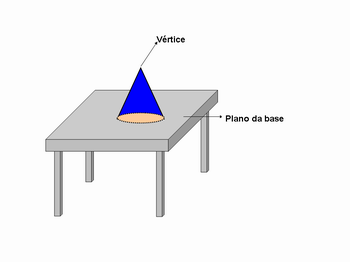
O professor pode apoiar o cone na mesa chamando o tampo da mesa de plano da base e pedir para o aluno apontar o que tem no plano oposto, ( onde fica a ponta do cone). Destacar que a “ponta do cone” é representada por um ponto e dar o nome de “VÉRTICE”, conforme mostrado abaixo.
(B) Elas têm a mesma forma? Se tiverem, em que se diferenciam?
NOTA:
Essa questão é para reforçar que todos os corpos redondos apresentados têm uma base circular, portanto, são parecidas. A diferença entre elas está apenas no tamanho das dimensões (comprimento, largura e altura).
(C) Como se chamam os corpos redondos que vocês separaram?
NOTA:
O professor deve apresentar essas figuras – sólido geométrico (corpo redondo) - que têm uma base circular e um ponto não pertencente ao plano da base chamada de vértice – nomeando-as como cones e, em seguida, pedir aos grupos que conceituem cones, representando-os em diferentes desenhos.
(D) Portanto, cone é:
............................................................................................................................................. ............................................................................................................................................. .............................................................................................................................................
III) ESFERA
O professor deverá entregar uma ficha que contenha as seguintes questões:
(A) Existem corpos geométricos que não têm base? Eles são parecidos com que objetos?
NOTA:
O professor deve mostrar que todos os objetos que têm formato de uma bola, geometricamente, são denominados de esfera. O conceito de esfera deve ser reforçado intuitivamente por meio da visualização de objetos e imagens.
EXEMPLOS DE ESFERAS
(B) Portanto, esfera é:
............................................................................................................................................. ............................................................................................................................................ ............................................................................................................................................
2ª ATIVIDADE - Grupos de 5 alunos
Nessa atividade, os alunos deverão distinguir os diferentes corpos redondos e poliedros. Para isso, o professor deve orientá-los, com antecedência, para que providenciem diferentes sólidos (cones, prismas de bases diferentes, troncos de sólidos geométricos,etc.) para esta aula. Este material deve também ser providenciado pelo professor, caso algum aluno não o tenha em mãos.
PARTE I: CLASSIFICAÇÃO DOS POLIEDROS
I) PRISMAS
1) Os grupos deverão distribuir os poliedros sobre a mesa do professor.
NOTA:
O professor deve retomar com os alunos o conceito de poliedro: “sólido geométrico delimitado por figuras planas não circulares (polígonos)".
1) O professor deve então entregar ao grupo uma ficha que contenha questões como as listadas a seguir:
(A) Separe os objetos que têm duas bases paralelas. Desses, destaque aqueles que têm bases congruentes.
NOTA:
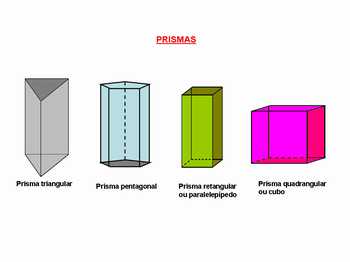
Nesse item, os alunos deverão separar os diversos poliedros na forma de: latas, embalagens, etc. O professor deve providenciar objetos que lembrem prismas para o caso de não haver material suficiente e/ou com bases diferenciadas, na forma de: hexágonos, pentágonos, triângulos etc., conforme desenho abaixo.
(B) Por que os poliedros escolhidos têm bases congruentes? Escolhendo um deles, qual é a forma das bases? ............................................................................................................................................. ............................................................................................................................................. .............................................................................................................................................
NOTA:
1) O professor deve reforçar a noção de congruência por sobreposição, como feito anteriormente com o cilindro, enfatizando agora os diferentes formatos na forma de polígonos.
2) O professor deve também observar que em um mesmo poliedro as bases são iguais, no entanto, em poliedros distintos as bases são de formas diferentes (Hexágonos, triângulos, etc.) ou de tamanhos diferentes.
(C) Escolha três poliedros de formas diferentes e escreva qual é a forma de cada face lateral. ............................................................................................................................................. ............................................................................................................................................. .............................................................................................................................................
NOTA:
O aluno deve observar que todas as faces têm a forma de um quadrilátero, sendo que:
1) se for um cubo a face é quadrada.
2) se for um paralelepípedo a face é um retângulo.
3) se for um poliedro oblíquo (inclinado) a face é um paralelogramo, (é mais difícil encontrar objetos no cotidiano de forma oblíqua, nesse caso, se o professor se interessar, pode providenciar um sólido em acrílico ou de cartolina com essa característica).
(D) Depois dessas observações, o professor apresenta a denominação dessas figuras como sendo PRISMAS. A seguir, orienta os alunos que desenhem alguns desses sólidos e registrem na ficha as características dessas figuras. Algumas dessas características podem ser, por exemplo: “Prismas são poliedros, têm duas bases congruentes paralelas, com faces laterais na forma de quadriláteros”.
(E) O professor deve, nesse momento, classificar esses prismas. Desse modo, deve fazer questionamentos como os especificados a seguir.
NOTA:
Esse trabalho pode ser desenvolvido por meio de fichas que serão entregues, pelo professor, uma a uma, a cada aluno, que em grupo, deve discutir as questões, as quais serão socializadas com toda a turma.
(F) Se todos esses objetos representam um prisma, onde está a diferença entre eles? ............................................................................................................................................. ............................................................................................................................................. .............................................................................................................................................
(G) Como então podemos chamá-los?
............................................................................................................................................. ............................................................................................................................................. .............................................................................................................................................
NOTA:
1) O professor deve explorar a linguagem dos alunos, pedir para que leiam suas frases, valorizar sua fala, e intervindo de modo a fazê-los observar que é a forma da base que nomeia o prisma, como, por exemplo:
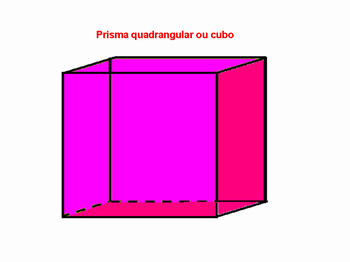
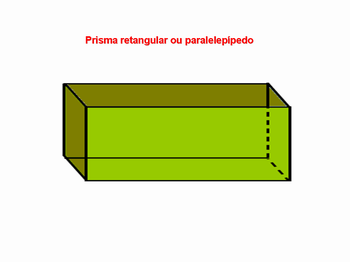
Se o aluno falar que o prisma a seguir é um quadrado, o professor deve intervir falando que quadrado é um polígono, que o poliedro em questão é um prisma de base quadrada ou um prisma quadrangular ou, como um caso especial, é um cubo.
2) O professor deve também destacar o nome “paralelepípedo” para o prisma retangular reto.
II) PIRÂMIDES
1) Os grupos deverão novamente distribuir os poliedros sobre a mesa.
NOTA:
O professor deve retomar com os alunos o conceito de poliedro: “sólido geométrico delimitado por figuras planas não circulares (polígonos)".
2) O professor deve então entregar ao grupo um estudo que contenha questões como as listadas a seguir:
A) Separe os objetos que têm apenas uma base.
NOTA:
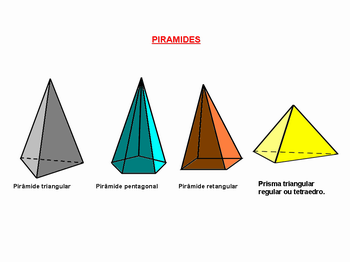
Nesse item, os alunos deverão separar os diversos poliedros na forma de: latas, embalagens etc. O professor deve providenciar objetos que lembrem pirâmide para o caso de não haver material suficiente e/ou com bases diferenciadas, na forma de: hexágonos, pentágonos, triângulos, etc., conforme desenho abaixo. Pirâmide triangular, Pirâmide pentagonal, Pirâmide retangular, Pirâmide triangular regular ou tetraedro.
NOTA:
O professor deve salientar que “esses poliedros não são prismas” porque não possuem duas bases. No entanto, em poliedros distintos as bases são de formas diferentes (Hexágonos, triângulos, etc.) ou de tamanhos diferentes.
C) Entregar fichas para registro das questões destacadas nos itens a seguir:
D) Nesses poliedros, qual a forma das bases?
............................................................................................................................................. ............................................................................................................................................. .............................................................................................................................................
E) Se você escolher três poliedros de formas diferentes, qual é a forma de cada face lateral? ............................................................................................................................................. ............................................................................................................................................. .............................................................................................................................................
NOTA:
O aluno deve observar que independente do poliedro todos os objetos têm faces de forma triangular.
3) Depois dessas observações, o professor deve dizer o nome desses sólidos: PIRÂMIDE. A seguir, pedir aos alunos que desenhem alguns desses sólidos e que registrem na ficha apresentado suas características tais como: “Pirâmides são poliedros que têm apenas uma base e todas as faces laterais na forma de triângulos”. Ao terminarem o registro dessas propriedades, os alunos devem socializar com a turma.
F) O professor deve classificar essas pirâmides. Desse modo fazer os questionamentos a seguir.
NOTA:
Esse trabalho pode ser desenvolvido por meio de fichas que serão entregues, pelo professor, uma a uma, a cada aluno que, em grupo, deve discutir as questões, as quais serão socializadas com toda a turma.
4) Se todos esses objetos representam uma pirâmide, onde está a diferença entre eles? ............................................................................................................................................. ............................................................................................................................................. .............................................................................................................................................
5) Como então podemos chamá-los?
............................................................................................................................................. ............................................................................................................................................. .............................................................................................................................................
NOTA:
1) Como na atividade anterior, o professor deve explorar a linguagem do aluno, pedir para que leiam suas frases e valorizar sua fala.
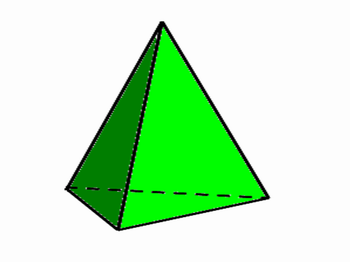
Se o aluno falar que a pirâmide a seguir é um triângulo, o professor deve intervir falando que triângulo é uma figura plana, um polígono. O poliedro em questão é um prisma de base triangular ou pirâmide triangular, conforme o desenho mostrado a seguir:
2) O professor deve também destacar o nome tetraedro, pirâmide de quatro faces na forma de triângulos equiláteros.
6) Pedir para os alunos colarem todas as observações no caderno.
7) Para finalizar a atividade, o professor poderá propor um jogo de memória, confeccionado pelos grupos e conferido pelo professor, o qual deve ser trocado entre eles para ser jogado.
8) Pode-se também desenvolver atividades disponíveis em:
http://www.malhatlantica.pt/saobruno/Ano08/mat/html_solidos/solidos_geometr.htm
Acessado em: 15 de novembro de 2010
Recursos Complementares
O professor poderá ainda realizar diversas atividades e curiosidades disponíveis em:
http://www.pedagogia.com.br/atividade.php?id=106 Acesso em: 15 de novembro de 2010
http://www.malhatlantica.pt/saobruno/Ano08/mat/html_solidos/modelos_poliedr.htm
Acesso em:15 de novembro de 2010
http://www.educ.fc.ul.pt/icm/icm99/icm21/poliedros.htm Acesso em: 15 de novembro de 2010
http://www.slideshare.net/guestb1469170/curiosidades-sobre-as-pirmides-de-giz Acesso em: 15 de novembro de 2010
Avaliação
A avaliação se dará por meio de observação, pelo professor, do desempenho dos alunos e do registro feito por eles a partir das atividades realizadas, verificando ainda se foram capazes de:
- diferenciarem pirâmides de prismas a partir de suas características;
- classificarem os corpos redondos em esferas, cones e cilindros.
Três estrelas 4 classificações
- Cinco estrelas 2/4 - 50%
- Quatro estrelas 1/4 - 25%
- Três estrelas 0/4 - 0%
- Duas estrelas 0/4 - 0%
- Uma estrela 1/4 - 25%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
emanuel, colegio sagrado coraçao de jesus , Tocantins - disse:
emanuelmartins104@gmail.com20/02/2015
Cinco estrelasFoi otimo
-
george correa, intituição do Colégio santo Antonio , Pará - disse:
georgecorrea34@gmail.com11/09/2012
Uma estrelaé até interessante só que não tem muitas gravuras tipo corpos redondos tem mas texto doq gravuras.
-
Geraldo Carvalho, Colegio Abaco , São Paulo - disse:
geraldo.carvalho1974@gmail.com16/08/2012
Quatro estrelasmuito bom,ajudou o meu filho...grato
-
Renata Esperança Rodrigues, Escola Estadual Daniel Ribeiro Moggi , Minas Gerais - disse:
reesrodrigues@hotmail.com02/04/2011
Cinco estrelasGostei da aula, bem interessante
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus