09/12/2010
Edson Luis Nunes, José Marcelo Gomes, Daniel Rodrigues Ventura.
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Física | Movimento, variações e conservações |
| Educação de Jovens e Adultos - 2º ciclo | Ciências Naturais | Visões de mundo |
O que o aluno poderá aprender com esta aula
· Conceituar energia mecânica de um sistema.
· Verificar que num sistema de forças conservativas, a energia mecânica se mantém constante.
· Definir ou conceituar o significado de força conservativa.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Trabalho de uma força, Energia cinética, Energia potencial gravitacional, relação trabalho e energia, força conservativa.
Estratégias e recursos da aula
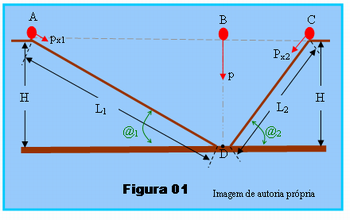
Sugerimos que inicialmente o professor apresente para a turma o esquema que está representado na Figura 01, explicando o que está sendo indicado por esta figura. Ela ilustra um corpo esférico, em três situações, correspondente às posições A, B e C, nessas posições o corpo será abandonado e deverá atingir o ponto D; pela rampa de comprimento L1 ao ser abandonado em A, verticalmente ao ser abandonado em B e pela rampa de comprimento L2 quando abandonado no ponto C. Em cada situação está representada a força resultante no corpo, sendo que nas rampas a resultante corresponde à componente do peso paralela a rampa, pois a outra componente do peso, perpendicular à rampa é anulada pela reação normal da superfície da rampa sobre o peso.
Atividade I
A partir das ilustrações considere m a massa do corpo, sendo g a aceleração da gravidade e despreze quaisquer forças de atrito. Com essas considerações peça aos alunos que individualmente ou em duplas calcule o trabalho realizado pela força de gravidade, peso do corpo, em função de m e g, nas três situações A, B e C indicadas na figura.
Deverão assim resolver o exercício.
Ao ser abandonado em A:
- WA = px.L1; px = p.sen@1 = p.H/L1 = mg.H/L1
- WA = mg.(H/L1).L1
- WA = mgH
Ao ser abandonado em B:
- WB = p.H
- WB = mg.H
Quando abandonado na posição C:
- WC = px.L2; px = p.sen@2 = p.H/L2 = mg.H/L2
- WC = mg.(H/L2).L2
- WC = mgH
Observa-se que nos três casos o trabalho da força peso teve o mesmo valor. O trabalho da força peso quando o corpo se desloca de um nível horizontal para outro é igual ao produto do peso do corpo pela diferença de nível, ou seja, pela distância vertical entre os dois níveis, altura H, independente do caminho pelo qual o corpo foi transportado. Forças com essas propriedades, ou seja, o trabalho por elas realizado depende apenas dos pontos, inicial e final, independente de quais pontos intermediários o corpo passou, são denominadas de forças conservativas. Em mecânica, o peso e a força elástica são exemplos de forças conservativas.
Atividade II
Após explicações acima, o professor deverá argumentar com a turma que quando num sistema todas as forças que nele se manifestam são forças conservativas, a energia mecânica do sistema permanece constante. Deve-se recordar com os alunos que energia mecânica é a soma das energias potencial e cinética. Assim sendo, em um sistema de forças conservativas, Em é constante, ou seja, Ep + EC = constante; Ep é a energia potencial e EC a energia cinética do sistema.
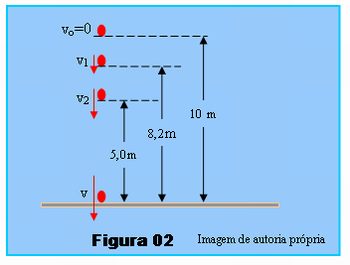
O professor poderá então elaborar um problema em que se manifestam apenas forças conservativas para que seja aplicado o princípio de conservação da energia mecânica. Considere por exemplo o esquema da Figura 02, em que um objeto é abandonado de uma altura de 10 m e peça aos alunos que resolvam individualmente o exercício abaixo.
Considere o esquema da Figura 02 em que um objeto é abandonado de uma altura de 10 metros acima do solo. Desprezando a força de resistência do ar e fazendo g = 10 m/s2, responda:
1. Qual o valor da velocidade v1 que ele passará pelo ponto de 8,2 m de altura?
2. E o valor da velocidade v2 quando estiver a 6,8 m do solo?
3. Com que velocidade, v no esquema, deverá atingir o solo?
Solução do problema:
· A energia mecânica, Em, deverá ter o mesmo valor em um instante qualquer, ou em qualquer posição, uma vez que a única força que atua no objeto é seu peso que é uma força conservativa, logo:
· Epo + ECo = Epx + ECx; Epo é a energia potencial inicial, ECo é a energia cinética inicial, Epx é a energia potencial num ponto x qualquer da trajetória e ECx é a energia cinética em um ponto x qualquer da trajetória.
No ponto a 8,2 m de altura, x = 8,2 m.
- Epo + ECo = Epx + ECx,
- mgH + mvo2/2 = mgx + mv12/2 (dividindo tudo por m)
- gH + vo2/2 = gx + v12/2
- 10.10 + 0 = 10.8,2 + v12/2
- 100 = 82 + v12/2
- 100 - 82 = v12/2
- 18 = v12/2
- 36 = v12
- v1 = 6 m/s
No ponto a 5,0 m de altura, x = 5,0 m.
- Epo + ECo = Epx + ECx,
- Epo mgH + mvo2/2 = mgx + mv22/2 (dividindo por m)
- gH + vo2/2 = gx + v22/2
- 10.10 + 0 = 10.5,0 + v22/2
- 100 = 50 + v22/2
- 100 - 50 = v22/2
- 50 = v22/2
- 100 = v22
- v2 = 10 m/s
3. No momento em que toca o solo, x = 0.
- Epo + ECo = Epx + ECx,
- Epo mgH + mvo2/2 = mgx + mv2/2 (dividindo tudo por m)
- gH + vo2/2 = gx + v2/2
- 10.10 + 0 = 0 + v2/2
- 100 = v2/2
- 200 = v2
- v = 14,1 m/s
Atividade III
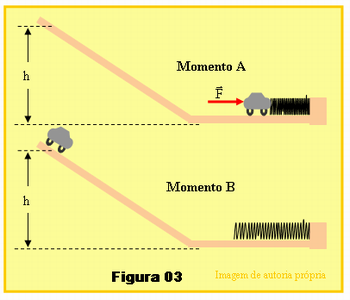
Considere agora a Figura 03 abaixo onde um carrinho é encostado e empurrado por uma força F contra a extremidade de uma mola. A outra extremidade da mola, oposta ao carrinho, está fixada num suporte e a força F empurra o carrinho até que a mola sofra uma deformação x igual a 20 cm, permanecendo parado nesta situação, Momento A, na figura. Em um dado momento o carrinho é solto, a mola se distende empurrando o carrinho que adquire velocidade subindo a rampa até atingir uma altura h, Momento B também indicado na figura. Se o professor conseguir um carrinho e uma mola poderá montar uma rampinha com uma tábua e fazer a montagem da figura. Na prática estará presente o atrito, força dissipativa, mas não tira o mérito do experimento, o professor poderá justificar que se houver variação da energia mecânica é devido a presença do atrito, que é força dissipativa, normalmente transformando parte da energia mecânica em calor, som, etc.
O professor então deverá propor aos alunos que desprezando a existência de quaisquer forças dissipativas, calcule o valor de h. Se o experimento for realizado use os valores obtidos, se não for feito o experimento forneça os seguintes dados: constante elástica da mola igual a 2000 N/m, massa do carrinho igual a 100 gramas, g igual a 10 m/s2.
Pela conservação da energia mecânica:
· Emi = Emf (Energia mecânica inicial é igual a energia mecânica final)
· Epe = Epg (Energia cinética inicial e final é nula, nesses pontos o carrinho se encontra parado).
· K.x2/2 = mgh
· 2000.(0,20)2/2 = 0,100.10.h (Unidades no SI)
· 1000.0,040 = h
· h = 40 m
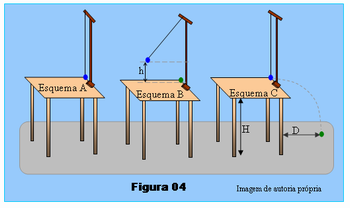
Depois o professor poderá fazer a seguinte montagem representada no esquema da Figura 04, abaixo. Um suporte sobre a mesa e pendurado neste suporte uma esfera, cor azul, através de um fio inextensível, de modo que na posição de equilíbrio fique sobre a mesa, bem próxima a beirada da mesa e também o mais próximo possível da superfície da mesa, contudo sem tocá-la, Esquema A da figura. Pode ser usado, por exemplo, um fio de nylon destes utilizado para pescar e uma bolinha de borracha que deve ser presa ao fio de nylon. A bolinha azul é puxada até atingir certa altura h, acima da posição de equilíbrio, Esquema B da Figura 04, e nessa condição, coloca-se sobre a mesa na posição referente à vertical de equilíbrio da bolinha azul, outra bolinha idêntica a ela, bolinha verde no esquema. Abandona-se então a bolinha azul e deixa que esta colida frontalmente com a bolinha verde. Marque então o ponto onde a bolinha verde toca o piso e marque a distância D, Esquema C; D é a distância horizontal desde a vertical que passa pela beirada da mesa até o ponto onde a bolinha toca o solo. H corresponde à altura da mesa.
Peça aos alunos que meçam as alturas h, H e D usando uma fita métrica ou uma trena; depois considere que quando a bolinha azul colide com a verde, a bolinha verde adquire velocidade igual à velocidade da bolinha azul no momento em que elas se tocam, e com os dados obtidos calculem:
- A velocidade horizontal da bolinha verde.
- A energia cinética inicial da bolinha verde em função de sua massa M.
- A energia potencial gravitacional da bolinha azul em função de sua massa M, relativa ao tampo da mesa no instante correspondente ao Esquema B.
- Compare os resultados obtidos nos itens 2 e 3 e tire sua conclusão.
Para resolver os itens acima, vamos supor que as medidas encontradas sejam h=20 cm = 0,20 m; H = D = 80 cm = 0,80 m. Com estes valores e fazendo g = 10 m/s2 obtém-se:
1. Para achar o tempo de queda da bolinha verde, faz-se necessário determinar o tempo de queda dela, então usando a equação:
- H = g.t2/2
- 0,80 = 10.t2/2 (SI)
- t2 = 0,16
- t = 0,4 s
Na horizontal o movimento é uniforme:
- D = vx.t
- 0,80 = vx.0,40
- vx = 2,0 m/s
2. A energia cinética inicial da bolinha verde:
- ECo = M.(2,0)2/2
- ECo = M.4,0/2
- ECo = 2M
3. A energia potencial da bolinha azul no esquema B:
- Ep = M.g.h
- Ep = M.10.0,20
- Ep = 2M
Verifica-se com esses resultados que a energia potencial inicial da bolinha azul foi totalmente transferida para a bolinha verde, houve conservação da energia mecânica do sistema.
Sugerimos que o professor assista aos vídeos, disponíveis na internet e se for possível repasse esses filmes para que os alunos possam assistir. Estes filmes são de pouca duração, 6 e 8 minutos respectivamente, apresenta excelentes ilustrações, com uma ótima didática e sem dúvida atrai atenção do aluno; Esses podem ser acessados com os seguintes títulos e endereços a seguir:
Novo Telecurso - Ensino Médio - Física - Aula 16 (1 de 2): 6 minutos
http://www.youtube.com/watch?v=DRW7yTRxb14
Novo Telecurso - Ensino Médio - Física - Aula 16 (2 de 2): 8 min e 18 s
Recursos Complementares
Sugerimos que o professor acesse o seguinte vídeo que é um experimento semelhante à montagem sugerida na Figura 04, porém com um material bem mais estruturado o que torna a exposição mais interessante e atrativa. O vídeo se encontra disponível na internet no seguinte endereço:
Mago da Física - Colisões (Um Exemplo Didático e Lúdico): 6 min e 10 s
http://www.youtube.com/watch?v=mrtMQ4MaLDQ
Sugerimos também que o professor acesse e confira o site abaixo que é uma animação simulando o princípio da conservação da energia mecânica, é bem interessante e se encontra disponível no endereço abaixo:
http://portaldoprofessor.mec.gov.br/fichaTecnica.html?id=10342
Avaliação
Os exercícios sugeridos durante a evolução da aula já são suficiente para avaliar se os alunos assimilaram o conteúdo, mas o professor ainda poderá elaborar outros exercícios referentes a esse assunto para que a turma resolva.
Também seria bom pedir que os alunos façam uma pesquisa sobre transformação e conservação da energia em um sistema.
Sem estrelas 0 classificações
- Cinco estrelas 0/0 - 0%
- Quatro estrelas 0/0 - 0%
- Três estrelas 0/0 - 0%
- Duas estrelas 0/0 - 0%
- Uma estrela 0/0 - 0%
Denuncie opiniões ou materiais indevidos!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus