17/12/2010
Edson Luis Nunes, José Marcelo Gomes, Daniel Rodrigues Ventura.
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Educação de Jovens e Adultos - 2º ciclo | Ciências Naturais | Visões de mundo |
| Ensino Médio | Física | Movimento, variações e conservações |
O que o aluno poderá aprender com esta aula
· Analisar o movimento harmônico simples MHS.
· Conceituar um MHS.
· Avaliar a variação da velocidade, da aceleração e da energia em um MHS.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Movimento Periódico, Energia Potencial, Energia Cinética, Vetores, Leis de Newton, Pêndulo simples, Força elástica.
Estratégias e recursos da aula
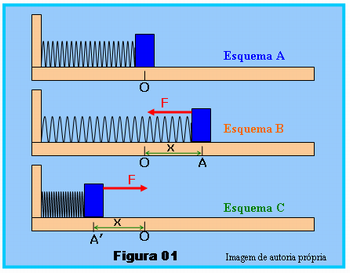
Sugerimos que o professor inicie sua aula apresentando e explicando para a turma a Figura 01, que corresponde ao esquema de uma mola apoiada em um plano horizontal tendo uma de suas extremidades fixa, presa em um ponto onde se encosta, e a outra extremidade acoplada a um bloco que pode oscilar livremente sobre o plano horizontal. Esse sistema possui um ponto de equilíbrio, comprimento natural da mola, ponto O. Quando o bloco preso à mola é afastado do ponto de equilíbrio surge uma força de sentido apontando para o ponto O. A força F que a mola exerce no bloco é F = -kx, em que o sinal negativo indica que F e o deslocamento da mola x tem sentidos opostos, conforme pode ser observado na figura. O peso do bloco e a força de reação da superfície de apoio sobre o bloco não estão representados na figura, estas forças se anulam.
No esquema A da figura, a mola se encontra em posição tal que seu comprimento é o natural não havendo esforço algum sobre ela, posição de equilíbrio, ponto O, no esquema.
No esquema B, a mola é esticada de forma a sofrer uma elongação x, variação em seu comprimento; x = L - Lo, Lo é o comprimento inicial, natural da mola e L seu comprimento final após ser distendida ou comprimida, posição A neste esquema.
No esquema C, a mola é comprimida de forma a sofrer uma compressão x, x = L - Lo como anteriormente, posição A’ no esquema C da figura.
Após comentários da Figura 01 o professor deverá explicar que a força elástica é uma força conservativa e que se no sistema o atrito for nulo, abandonando o bloco na posição A do esquema da figura, ele oscilará preso à mola passando pelo ponto O chegando até A’ e retornando passando novamente no ponto O até atingir A novamente. Nesse movimento quando o móvel passa novamente pelo mesmo ponto repetindo o movimento dizemos que ele executou um ciclo completo. Sem interferência externa, o movimento cíclico se repetirá indefinidamente.
A distância máxima a partir do ponto de equilíbrio O, ou seja, a elongação máxima x, x = A, é denominada de amplitude do movimento. O movimento é um movimento harmônico simples, MHS; é um movimento que oscila periodicamente em torno de um ponto de equilíbrio. O tempo gasto para executar um ciclo completo é denominado de período, normalmente representado pela letra T. O número de ciclos completados na unidade de tempo corresponde à freqüência f do movimento, tem-se que f = 1/T.
Atividade I
O professor após explicações acima deve fornecer valores da constante elástica da mola, da variação do comprimento x, elongação da mola, da massa do bloco e pedir aos alunos que resolvam individualmente numa folha ou caderno, o seguinte exercício.
Na Figura 01 calculem os valores da aceleração do bloco nos pontos A, O e A’. Considere: k = 20 N/m, x = 20 cm e m = 1,0 kg.
Deverão responder, considerando o sentido positivo para a direita:
No ponto A:
- a = F/m; F = -kx.
- a = -k.x/m
- a = -20.0,20/1,0 (Unidade no SI)
- a = -4 m/s2, ou seja, 4 m/s2 para a esquerda.
No ponto O:
- x = 0; F = -kx = 0
- a = 0
No ponto A’:
- a = F/m; F = -kx.
- a = -k.x/m
- a = -20.(-0,20)/1,0 (Unidade no SI)
- a = 4 m/s2, ou seja, 4 m/s2 para a direita.
O professor então deverá expor para os alunos que abandonando inicialmente o bloco no ponto A, este iniciará seu movimento sendo acelerado para a esquerda. A força da mola e em conseqüência a aceleração vai diminuindo com a diminuição de x até quando x se torna nulo no ponto O. Enquanto tiver aceleração no mesmo sentido da velocidade, o valor da velocidade do bloco aumentará até que atinja o ponto O, quando a força elástica se anula, aceleração igual a zero.
Ao passar pelo ponto O, o bloco por inércia continua se movendo para a esquerda, mas após passar pelo ponto O, a mola está sendo comprimida e começa a forçar o bloco em sentido oposto ao seu movimento, fazendo com que sua velocidade diminua até parar no ponto A’ quando o movimento inverte seu sentido. O bloco então é acelerado para a direita e sua velocidade vai aumentando até que a força da mola se anula no ponto O. Por inércia, o bloco continua a mover para a direita, e a mola é esticada forçando o bloco para esquerda, diminuindo sua velocidade e fazendo-o parar no ponto A, quando a velocidade se anula e recomeça todo o ciclo novamente.
O professor deverá esclarecer que o movimento harmônico simples pode ser visto como a projeção ortogonal do movimento circular uniforme sobre uma reta. Considerando o esquema ilustrado na Figura 01, relacionando com um MCU de raio igual a A, através de algumas adequações matemáticas que não serão exploradas nesta aula, obtém-se a seguinte expressão de x em função do tempo: x = A.cos(wt), em que w é a velocidade angular do MCU correspondente, w = 2p.f, sendo p = 3,14 e f a freqüência do movimento; t é o tempo a partir do instante em que o bloco é abandonado na posição A.
Atividade II
Usando a expressão de x em função do tempo por meio de cálculo diferencial, normalmente não usado no ensino médio, encontram-se as seguintes expressões para a velocidade v e para a aceleração a, no MHS: v = -wA.sen(wt) e a = -w2A.cos(wt).
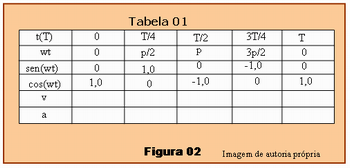
Após essas explicações o professor deverá pedir que os alunos individualmente ou em duplas copiem numa folha a Tabela 01 da Figura 02 abaixo, e preencham as lacunas em branco da tabela, calculando os valores da velocidade v do bloco e da aceleração a, em função de w e A.
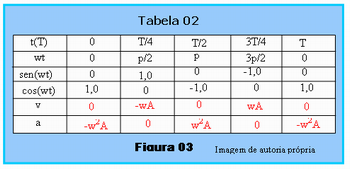
Para resolver o exercício, os alunos deverão substituir os valores de sen(wt) e cos(wt) em cada caso para preencher as lacunas da Tabela 01 na Figura 02. Usando as expressões v = -wA.sen(wt) e a = -w2A.cos(wt), deverão encontrar os seguintes valores, que se encontram preenchidos na tabela 02 da Figura 03.
O professor então deverá pedir aos alunos que com os dados obtidos na Tabela 02 da Figura 03, tracem os gráficos da velocidade (v) em função do tempo t e da aceleração (a) em função de t.
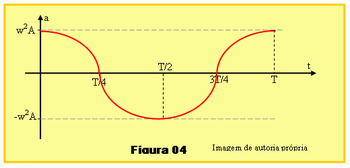
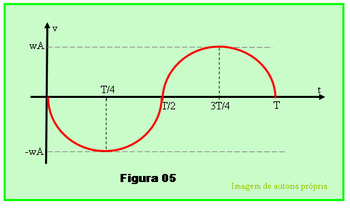
Para explicar e fazer a correção dos gráficos de aXt e vXt referentes a Tabela 02 da Figura 03, o professor poderá utilizar a Figura 04 e a Figura 05, mostrar esses gráficos, e explicar que, como a função da velocidade e da aceleração são funções do seno e do cosseno, o gráfico que representam essas grandezas tem seu aspecto característicos das curvas dessas funções trigonométricas, conforme essas figuras.
Após correção dos gráficos o professor deverá reforçar com os alunos que sobre o bloco atuando apenas a força da mola, a energia mecânica do sistema se conserva. Temos então que em qualquer instante ou em qualquer ponto tem-se: Ep + Ec = Em. Para encontrar o valor da energia mecânica do sistema, Em, podemos determinar seu valor no ponto A: Em = EpA + EcA; EpA = k.A2/2 e EcA = 0, ou seja, Em = k.A2/2.
Tem-se então para um instante t qualquer ou em um ponto qualquer que: Ep = k.x2/2 e Ec = Em – Ep, segue portanto, Ec = k.A2/2 - k.x2/2 ou seja, Ec = (k/2)(A2 - x2).
Atividade III
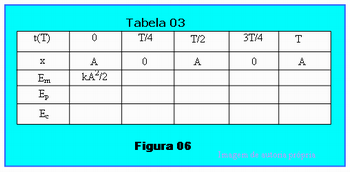
Com todas essas informações o professor deverá mostrar a Tabela 03 da Figura 06 e pedir que os alunos copiem essa tabela numa folha e preencham as lacunas em branco na tabela.
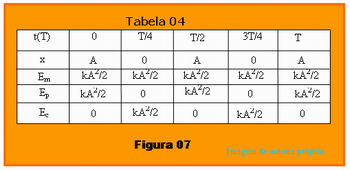
A Figura 07 é a Tabela 04 que corresponde a Tabela 03 com as lacunas já preenchidas. Para correção do exrcício proposto acima, o professor poderá utilizar essa figura, Tabela 04, que é a solução do exercício anterior.
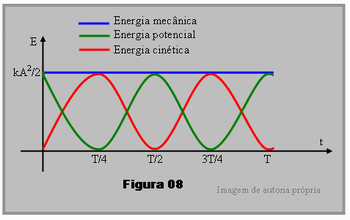
Depois o professor deverá pedir para os alunos que usando a tabela 04, Figura 07, trace o gráfico de energia em função do tempo para um período completo do MHS, fazendo no mesmo gráfico as curvas correspondentes da energia mecânica, da energia potencial e da energia cinética.
Como solução o professor poderá utilizar o gráfico da Figura 08 onde pode ser verificado que a energia mecânica, energia total é constante, seu valor é o mesmo em qualquer instante durante todo o ciclo, linha reta azul. Verifica-se também que quando a energia potencial aumenta a energia cinética diminui, e vice versa, de tal modo que a soma das duas mantém o mesmo valor durante todo o ciclo, soma essa que corresponde à energia mecânica do sistema.
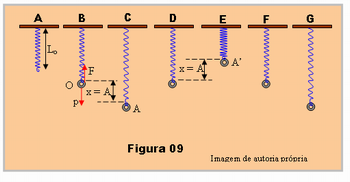
O professor poderá fazer uma demonstração qualitativa para mostrar como variam as grandezas que foram avaliadas no MHS, velocidade, aceleração, e energia mecânica. Para isso deve usar uma mola ou não conseguindo uma mola poderá substituí-la por um elástico e fazer a montagem apresentada na Figura 09. Nesta figura uma mola é pendurada em um suporte qualquer e seu comprimento natural é Lo, esquema A, à esquerda na figura.
No esquema B, um pequeno objeto, uma porca de parafuso, por exemplo, é presa na extremidade da mola ficando em equilíbrio no ponto O, peso do objeto = força elástica da mola.
No esquema C o objeto é puxado para baixo até a posição A e em seguida abandonando.
O objeto nesta posição sobe passando pela posição de equilíbrio, ponto O, esquema D.
Por inércia o objeto continua subindo sendo forçado para baixo sob ação de seu peso e pela força elástica da mola, sua velocidade então diminui até parar na posição A’, esquema E da figura.
O movimento inverte de sentido e começa a descer sendo acelerado até o ponto de equilíbrio O, esquema F.
Após passar o ponto O, a força elástica passa a ser maior que o peso diminuindo a velocidade do objeto que para no ponto A completando o ciclo. A partir daí recomeça o ciclo.
Portanto, nos pontos extremos A e A’ a velocidade é nula e a aceleração é máxima; no ponto O, que corresponde ao ponto de equilíbrio, a velocidade é máxima e a aceleração é nula.
Finalizando o professor poderá pedir aos alunos para formar grupos de 4 elementos e numa folha em branco resolver o exercício transcrito abaixo.
Um pequeno bloco de massa m = 0,20 kg oscila num plano horizontal sem atrito preso a uma mola de constante elástica k = 3,2 N/m. A energia mecânica do sistema é 0,016 J, determine para a posição de equilíbrio do sistema bloco mola e depois para o ponto de máxima elongação da mola.
- A aceleração do bloco.
- A energia potencial elástica da mola.
- A energia cinética da mola.
- A velocidade do bloco.
Deverão resolver o problema, considerando primeiro no ponto de equilíbrio do sistema bloco mola:
- No ponto de equilíbrio a força resultante é nula, condição de equilíbrio, logo a aceleração é nula; a = 0.
- Na direção horizontal a única força atuante no bloco é a força elástica, sendo a resultante nula indica que a força elástica é nula e nesse caso a energia potencial elástica também é nula; Ep = 0.
- Em = Ep + EC
- 0,016 = 0 + EC
- EC = 0,016
4. EC = m.v2/2
- 0,016 = 0,20.v2/2
- 0,016 = 0,10.v2 (Unidades no SI)
- v2 = 0,16
- v = 0,4 m/s
Considerando agora no ponto de máxima elongação da mola:
1. No ponto de máxima elongação da mola, v = 0 e EC = 0. Temos então, Ep = Em, mas Ep = k.x2/2
- K.x2/2 = 0,016 (SI)
- 3,2.x2 = 0,032
- X2 = 0,01
- X = 0,10 m
- a = k.x/m
- a = 3,2.0,10/0,20
- a = 1,6 m/s
2. Ep = Em, como visto no item anterior, logo, Ep = 0,16 J.
3. v = 0 , EC = m.v2/2, então; EC = 0.
4. v = 0
Recursos Complementares
Sugerimos que o professor acesse o endereço abaixo e assista a simulação que corresponde a variação da elongação, velocidade, aceleração, força e energia num movimento vertical de um objeto suspenso oscilando preso a uma mola, e se achar interessante apresentar esta simulação para os alunos.
http://www.walter-fendt.de/ph14br/springpendulum_br.htm
Outra simulação sobre fase, velocidade angular e amplitude pode ser acessada no seguinte endereço:
http://portaldoprofessor.mec.gov.br/fichaTecnica.html?id=15613
Avaliação
O professor pode elaborar exercícios para os alunos resolverem individualmente ou em equipes fora do horário de aulas, como por exemplo, pedir que façam os gráficos de velocidade, aceleração, energia cinética e potencial de um corpo que oscila preso a uma mola vertical, durante um ciclo completo, semelhante aos esquemas da Figura 09.
Sem estrelas 0 classificações
- Cinco estrelas 0/0 - 0%
- Quatro estrelas 0/0 - 0%
- Três estrelas 0/0 - 0%
- Duas estrelas 0/0 - 0%
- Uma estrela 0/0 - 0%
Denuncie opiniões ou materiais indevidos!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus