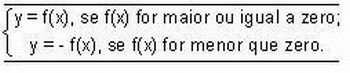14/01/2011
Fernando Celso Villar Marinho; Rita Maria Cardoso Meirelles; Jackson Lopes; Ivail Muniz Junior; Clayton Gonçalves Silva
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Álgebra |
| Ensino Médio | Matemática | Tecnologia para a matemática |
O que o aluno poderá aprender com esta aula
Relacionar o conceito de distância ao módulo ou valor absoluto de um número.
Identificar a lei de formação através da definição de módulo.
Trabalhar a construção de gráficos;
Determinar o domínio e a imagem da função.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Reta numerada;
Conceito de função.
Estratégias e recursos da aula
Professor, para realizar essa aula, encaminhe primeiramente os alunos ao laboratório de Informática, e peça que os alunos se acomodem em, no máximo, três alunos por computador.
Exiba, com o uso do Data Show, as imagens abaixo, que representam situações em que podemos utilizar a noção de distância no dia-a-dia.
Figura 1: Exemplo de distância - Estrada
Fonte: http://ts3.mm.bing.net/images/thumbnail.aspx?q=309010767558&id=9605c987cdb3327e67b5b04b84d619bf
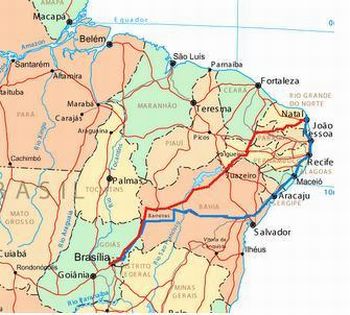
Figura 2: Exemplo de distância - Mapa
Fonte: http://ts4.mm.bing.net/images/thumbnail.aspx?q=303070194331&id=53881aaf04239a18040a19d7808e0915
Figura 3: Exemplo de distância – Placas indicativas
Fonte: http://ts4.mm.bing.net/images/thumbnail.aspx?q=323523196247&id=cc1ffed005627465e1e17216e5bc8fbb E
Peça para a turma analisar as imagens e pergunte se alguém passou pela experiência de, por exemplo, perguntar onde fica um determinado lugar e receber como resposta que o mesmo está a 5 km de distância. Esperamos que a turma observe que em todas as situações que envolvem o conceito de distância teremos como resposta um número positivo.
Solicite que a turma reflita sobre o mundo à sua volta e resgate outras situações do cotidiano onde o conceito de distância é utilizado, promovendo a seguir uma troca de ideias sobre o tema.
Atividade 1:
O objetivo da atividade, interativa e exploratória, é fazer com que o aluno trabalhe o conceito de módulo ou valor absoluto de um número associando-o ao de distância.
Exiba, com o uso do Data Show, a imagem abaixo que representa a reta numérica.
Figura 4: Reta numérica
Fonte: http://t3.gstatic.com/images?q=tbn:xUjHQp7ifBzh9M:http://1.bp.blogspot.com/_a8eVxCfyq70
Pergunte qual é a distância dos números -5 e 5 à origem.
A turma deve perceber que o número 5 está a uma distância de 5 unidades da origem, e que -5 também está a 5 unidades da origem.
Peça que eles criem outros exemplos. Em seguida, questione sobre as descobertas feitas pela turma, verificando se os alunos apreenderam, com êxito, os conceitos trabalhados.
Definindo Módulo ou Valor Absoluto:
Professor, peça que os alunos registrem em seus cadernos a definição:
O conceito de módulo ou valor absoluto de um número real está ligado à ideia de distância de um ponto da reta à origem. Como existe uma correspondência entre os pontos da reta e os números reais, quando nos referimos à distância de um ponto à origem ou ao módulo de um número, estamos nos referindo à mesma ideia.
Notação: |a|.
Usamos duas barras para representar o módulo de um número.
Professor, construa este conceito com a turma e, em seguida, apresente a figura abaixo.
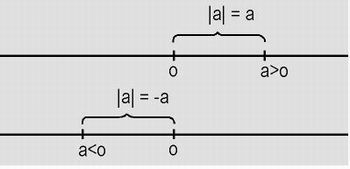
Figura 5: Construção do conceito de módulo
Fonte: http://ecalculo.if.usp.br/funcoes/modulo/img_modulo/graficomodulo.gif
Conclua com a turma:
Definindo Função Modular
Quando uma função é colocada dentro de um módulo, ela é denominada modular. Seu formato é dado por: y = |f(x)|.
Esta função pode ser substituída por outras duas funções que são equivalentes à função anterior:
Atividade 2:
Informe aos alunos que a atividade a ser realizada tem como objetivos a percepção e o entendimento de como podemos aplicar a definição de função modular para construir gráficos.
Considerando a função y = |x|:
a) Obtenha a lei de formação da função.
b) Construa o gráfico desta função.
c) Determine o domínio e a imagem da função.
Nota: Permita que os alunos troquem informações e, após realizada a atividade, confirme as soluções encontradas pela turma.
a)
b)
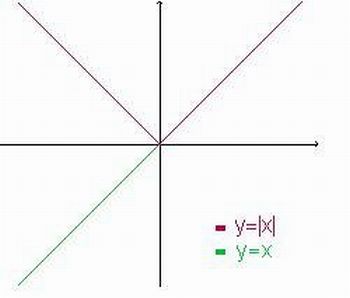
Figura 6: Gráfico da função
Fonte: http://ecalculo.if.usp.br/funcoes/modulo/img_modulo/image010.gif
c) O domínio é formado pelo conjunto dos números reais e a imagem é formada pelos números reais maiores ou iguais a zero.
Ou seja, D = R e Im = R+
Os alunos devem perceber que:
1) A função modular gera duas sentenças.
2) O gráfico de y = |x| coincide com a reta y = x para valores de x positivos ou nulo, enquanto que para valores negativos de x considera-se a semi-reta "rebatida" pois, nesse caso, |x| = –x.
3) Esta semi-reta "rebatida" é simétrica da original em relação ao eixo das abscissas.
Atividade 3:
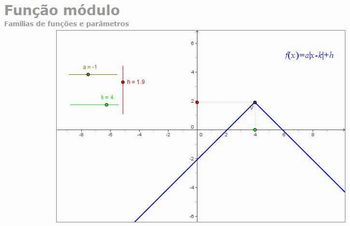
1) Informe aos alunos que a atividade a ser realizada tem como objetivos manipular e visualizar gráficos do tipo: f(x) = a|x – k| + h.
2) Para realização da mesma peça que acessem o recurso do portal:
 Função Módulo – Família de funções e parâmetros
Função Módulo – Família de funções e parâmetros
Figura 7: Trabalhando o gráfico da função modular
Fonte: http://mat.absolutamente.net/ra_f_mod.html
3) Permita que os alunos manipulem e façam descobertas por um tempo aproximado de 10 minutos e, em seguida, promova uma discussão a respeito das descobertas feitas.
A turma deve perceber que:
1. As alterações do parâmetro h, provocam translações verticais no gráfico, alterando, deste modo, o conjunto imagem da função.
2. As alterações do parâmetro k, provocam translações horizontais no gráfico.
3. As alterações do parâmetro a, modificam a "abertura"/"fechamento" do gráfico.
Recursos Educacionais
| Nome | Tipo |
|---|---|
| Função Módulo – Família de funções e parâmetros | Animação/simulação |
Recursos Complementares
Sites consultados : http://ecalculo.if.usp.br/
http://modulos.math.ist.utl.pt/html/funcdeprop12.shtml
Veja também as seguintes aulas que complementam este assunto:
- Plano Cartesiano como Ferramenta na Resolução de Equações e Inequações Modulares;
- Construindo os Conceitos de Função Composta, Injetora, Sobrejetora e Bijetora;
- Estudando Colônia de Bactérias para Construir o Conceito de Função Exponencial ;
- Abalos sísmicos e logaritmos;
- Análise gráfica e Criptografia: O Comportamento da função inversa.
Avaliação
Tal avaliação deve ser feita ao observar as dúvidas dos alunos durante a realização das atividades sugeridas acima onde o professor terá a oportunidade de verificar o nível de entendimento ao circular pelos grupos durante as atividades 1, 2 e 3.
Quatro estrelas 2 classificações
- Cinco estrelas 1/2 - 50%
- Quatro estrelas 1/2 - 50%
- Três estrelas 0/2 - 0%
- Duas estrelas 0/2 - 0%
- Uma estrela 0/2 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Luiz André, Seduc, Fibra e CIPP , Pará - disse:
andre.v.melo@gmail.com11/02/2014
Quatro estrelasGostei bastante.
-
moises da costa farias, pai de aluno , Goiás - disse:
moises.cfarias@hotmail.com05/04/2011
Cinco estrelasexcelente
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus