13/04/2011
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Fundamental Final | Matemática | Cálculo |
| Ensino Fundamental Final | Matemática | Números e operações |
O que o aluno poderá aprender com esta aula
- Desenvolver vocabulários relacionados à probabilidade;
- Contextualizar probabilidade e análise combinatória;
- Desenvolver o raciocínio combinatório, analisando quais e quantas são as possibilidades de algo ocorrer e resolver situações-problema que envolvam a ideia de possibilidade;
- Desenvolver o raciocínio de chance e de sua medida (probabilidade) e resolver situações-problema que envolvam o conceito de probabilidade;
- Interpretar razões, inclusive porcentagens, como medidas de probabilidade.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Razão e porcentagem.
Estratégias e recursos da aula
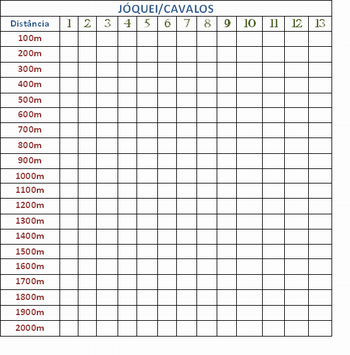
Iniciar a aula com uma corrida de cavalos
Dividir os alunos em grupos de 4 a 5 componentes. Cada grupo receberá uma folha (modelo abaixo) onde ocorrerá a corrida e dois dados (com faces de 1 a 6). Estabelecer um responsável para registrar o desempenho dos cavalos e outro para jogar os dados. Os participantes deverão ser avisados que os dados serão lançados e a soma destes indicará qual cavalo avançará na pista. Cada apostador/aluno terá o direito de escolher dois cavalos (para apostar cada participante recebe um papel/cédula para escrever o número dos cavalos e o porquê da escolha destes). Recolher as apostas. Ganhará o jogo quem escolher o cavalo cujo número for sorteado mais vezes.
Após o jogo, comparar os resultados dos diferentes grupos, registrando no quadro/lousa os três cavalos melhores colocados em cada grupo. Perguntar o que observaram.
Muitos alunos escolhem os cavalos 1 e 13 ignorando completamente as possibilidades dos dados, deixando apenas critérios subjetivos interferirem na escolha sobre o melhor cavalo.
Demonstrar a probabilidade (buscar em um dicionário o significado da palavra) que cada cavalo tinha de ser sorteado em cada lançamento de dois dados.
Cavalo 1 - nunca;
Cavalo 2 - uma chance (1+1);
Cavalo 3 - duas chances (1+2) e (2+1);
Cavalo 4 - três chances (1+3), (3+1) e (2+2);
Cavalo 5 - quatro chances (1+4), (4+1), (2+3) e (3+2);
Cavalo 6 - cinco chances (1+5), (5+1), (2+4), (4+2) e (3+3);
Cavalo 7 - seis chances (1+6), (6+1), (2+5), (5+2), (3+4) e (4+3);
Cavalo 8 - cinco chaces (2+6), (6+2), (3+5), (5+3) e (4+4);
Cavalo 9 - quatro chances (3+6), (6+3), (4+5) e (5+4);
Cavalo 10 - três chances (4+6), (6+4) e (5+5);
Cavalo 11 - duas chances (5+6) e (6+5);
Cavalo 12 - uma chance (6+6);
Cavalo 13 - nunca.
Professor, peça aos alunos que escrevam a razão entre o número de chances de cada cavalo e o número total de possibilidades (36).
Note que o cavalo sete é o que possui a maior chance: 6/36 que equivale a 0,1666... ou 16,66%.
É importante observar que ao dividir as razões os valores obtidos estão situados entre 0 e 1. Por quê? (Em recursos complementares há um vídeo que aborda a questão).
Pode-se definir probabilidade como:
Medida da chance de ocorrência expressa como um número entre 0 e 1, onde 0 é a impossibilidade e 1 é a certeza absoluta.
Proponha aos alunos que calculem a chance, em porcentagem, de cada cavalo ser sorteado em cada lançamento de dois dados.
Comparar os resultados obtidos na corrida de cavalos com os obtidos no cálculo do percentual de chance de cada um. Se a brincadeira fosse novamente proposta, em quais cavalos apostariam agora?
Professor proponha um exercício para que seus alunos possam praticar um pouco. Em duplas, peça para que eles lancem uma moeda para o alto e anotem em uma tabela o números de jogadas, de caras e de coroas depois de jogadas 10, 20, 30 e 50 vezes. Em seguida, peça para que eles encontrem a razão entre o número de caras/coroas obtido e o número de lançamentos feitos e também o percentual de cada um.
Curiosidade:
- Buffon, cientista francês (1707 - 1788) lançou uma moeda 4.040 vezes, tendo obtido 2.048 caras, ou seja uma frequência relativa para a saída de cara de 0.5069;
- Por volta de 1900, o estatístico inglês Karl Pearson lançou uma moeda 24.000 vezes. Obteve 12.012 caras, ou seja, 0.5005 para a frequência relativa da saída de cara.
fonte: BIBODE, Antonio José L. Matemática hoje é feita assim. São Paulo: FTD, 2000. p. 307 - (Coleção Matemática hoje é feita assim).
Qual é o número de caras esperado, caso a moeda seja jogada 100 vezes?
Se em muitos lançamentos de uma moeda a frequência de caras observadas se aproxima de ½ então dizemos que a probabilidade da saída de cara num próximo lançamento será de ½ ou 50%.
Professor proponha as atividades abaixo para que seus alunos possam aplicar os conhecimentos abordados:
Atividade 1:
Numa feira costuma-se realizar um jogo no qual sempre se ganha um prêmio. Roda-se 3 vezes uma roleta numerada de 1 a 4 e somam-se os pontos obtidos. O prêmio é dado segundo o total obtido.
a) Os melhores prêmios são dados a quem obtém o total 1, 2, 3 ou 12. Você saberia dizer por quê?
b) A chance de se obter 10 pontos é maior do que a de se obter 8 pontos? Justifique.
Atividade 2:
Um jogo de computador chamado "Campo Minado" consiste em uma tela dividida em janelinhas inicialmente fechadas, como na ilustração abaixo. Abrindo-as, podem-se encontrar números, espaços vazios ou bombas. A quantidade de janelinhas é variável, assim como o número de bombas escondidas. No exemplo, são 256 janelas com 40 bombas escondidas. Clicando sobre uma janela com o botão esquerdo do mouse, abre-se uma ou várias janelas. Se dentro dela esconder-se uma bomba, a tela explode e perde-se o jogo, como na ilustração. No caso de ter certeza de que há uma bomba, deve-se clicar a janela com o botão direito do mouse, assim ela abrirá sem explodir a tela. O objetivo do jogo é abrir todas as janelas sem provocar a explosão.
a) Imagine-se jogando na tela do exemplo. Clicando ao acaso, qual a probabilidade de acertar uma janelinha que não tenha uma bomba escondia?
b) E qual a probabilidade de explodir a tela?
c) A tela mais avançada desse jogo é composta por 480 janelas que escondem 99 bombas. A iniciar o jogo nessa tela, clicando ao acaso, qual a probabilidade de não estourá-la?
Atividade 3:
Propor aos alunos os jogos "Sorteio na caixa" e "Roleta matemática", usando um objeto de aprendizagem interativo disponibilizado pelo portal do professor.
 Probabilidade: a matemática ao acaso
Probabilidade: a matemática ao acaso
Recurso disponível em: http://portaldoprofessor.mec.gov.br/fichaTecnica.html?id=917 (Dezembro/2010)
Jogos e brincadeiras como estas são inocentes e possibilitam o desenvolvimento de conceitos matemáticos. Mas que olhar devemos lançar sobre o jogo quando ele mexe com o imaginário de milhões de pessoas e envolve milhões em dinheiro como é o caso das chamadas loterias? Ao utilizar slogans do tipo: “acredite na sorte”, o que eles estão vendendo? Possibilidade ou ilusão? Será que as pessoas que apostam têm consciência do grau de dificuldade que está por traz destes jogos?
Dentre todas as loterias existentes no Brasil, a Mega-Sena é, ao menos em certas ocasiões, a que desperta o maior interesse na população. O jogo consiste em acertar 6 números dentre os 60 (1 a 60) disponíveis no volante (quem acerta 4 ou 5 também ganha), sendo possível marcar de 6 a 15 números na aposta.
Há na internet um artigo (abaixo) bem interessante sobre este jogo e que pode ser objeto de discussão na sala de aula:
COMO NÃO GANHAR NA MEGA SENA – Por José Antonio Francisco
No Brasil, as loterias seduzem milhões de pessoas a cada semana com a esperança de tornarem-se milionárias. É tão grande a fascinação, que jornais publicam quais números foram mais ou menos vezes sorteados e muitos apostadores tentam descobrir a “lógica” dos resultados dos sorteios. Mas há, realmente, alguma técnica para jogar, como defendem alguns, ou isso não passa de simples ilusão? A Mega-sena é um jogo de azar, pois não há como a habilidade do apostador interferir no resultado. Por que, então, contrariando essa condição, evitamos apostas em combinações sequenciais, ou formadas por números próximos um do outro? O raciocínio que norteia tal critério de aposta é o de que seria muito difícil ocorrer tais coincidências. Entretanto, o raciocínio correto é o de que a probabilidade de, em algum sorteio, saírem tais combinações especiais é a mesma de saírem quaisquer outras combinações. E isso demonstra o quanto é difícil acertar na Mega-sena: a probabilidade de ser sorteada uma combinação selecionada é a mesma de ser sorteada qualquer combinação especial (1, 2, 3, 4, 5 e 6, por exemplo). Portanto, imaginarmos que, afastando as combinações especiais, as probabilidades aumentam é pura ilusão. De fato, qualquer tentativa de previsão de resultados que se baseie na distribuição dos números no formulário não tem fundamento algum. Os números são apenas signos escolhidos para representar o resultado do sorteio. Poderiam ser substituídos por quaisquer outros símbolos, como desenhos de frutas, nomes de mulher, ou letras, e não precisariam estar em sequência. Além disso, o resultado da Mega-sena é uma combinação de seis números (o seu universo é de 50.063.860 de possíveis resultados), e considerar, de forma isolada, quantas vezes um número foi sorteado sequer tem significado estatístico. Em relação às estatísticas, a Matemática nos diz que um jogo como o da Mega-sena é regido por um processo que não tem “memória”. Isto significa que o resultado do evento anterior não exerce qualquer influência sobre o resultado do evento futuro (...) Por fim, poderíamos entender o significado da probabilidade de acertar na Mega-sena com um exemplo mais concreto. Se, durante 50 anos, jogássemos 100 jogos por dia de aposta (duas vezes por semana), nossa chance de acertar ao menos uma vez seria de pouco mais de 1%. Portanto, jogando duzentos reais por semana, durante 50 anos, nossa chance de não ganhar na sena seria de 99%. Portanto, aí está a receita para não ganhar na mega-sena: jogar toda semana, durante 50 anos, gastando 200 reais por semana (probabilidade de ganhar: menos de 1%).
fonte: http://www.sigmasociety.com/artigos/jose_antonio_francisco_megasena.pdf (Dezembro/2010)
Comparações como esta, possibilitam uma melhor compreensão do que significa essa probabilidade tão pequena. Podem ser feitas comparações com a possibilidade da ocorrência de outros eventos, ou ainda comparações com modelos geométricos, utilizando razões entre comprimentos, áreas ou volumes como analogias para uma probabilidade, já que esta também é uma razão.
Alguns exemplos:
- A população do Brasil é de quase quatro vezes o número de resultados possíveis do sorteio. Se fosse realizado um sorteio de quatro prêmios entre toda a população brasileira, a sua chance de ganhar um deles seria igual à de ganhar o prêmio máximo da Mega-Sena com um jogo de seis números.
- No Você sabia? da RPM 41 (Revista do Professor de Matemática), página 29, foi observado que é mais fácil obter 25 caras em 25 lançamentos de uma moeda do que ganhar na Mega-Sena com uma aposta de 6 números.
Proponha agora o cálculo e construção de outras comparações:
Atividade 4:
a) Se uma linha de um centímetro corresponder à probabilidade de acertar a sena no jogo da Mega-Sena (1 em 50.063.860), quantos quilômetros terá a linha que corresponderá a probabilidade de perder? Essa linha irá de sua cidade até que cidade?
b) A chance de ganhar na Mega-Sena é de 1 em 50.063.860. Agora imagine-se contando de 1 até o número que corresponde à chance de não ganhar. Se você fizer isso, contando um número por segundo e sem descanso, terminará a contagem daqui a quantos dias?
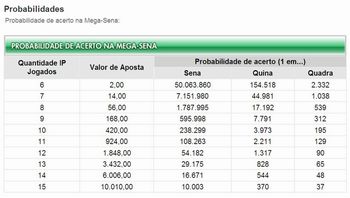
c) Proponha aos alunos que pesquisem ou criem comparações semelhantes a estas. Após, professor e alunos escolherão as que julgarem melhores e poderão publicar no site da escola, no mural, etc., como instrumento de informação e conscientização (no quadro abaixo é possível observar as chances de acerto na Mega-Sena).
fonte: http://www1.caixa.gov.br/loterias/loterias/megasena/probabilidades.asp (Dezembro/2010)
Recursos Educacionais
| Nome | Tipo |
|---|---|
| Probabilidade: a matemática ao acaso | Animação/simulação |
Recursos Complementares
Avaliação
Atividades em sala: observando o interesse, envolvimento e desempenho dos alunos.
Cinco estrelas 3 classificações
- Cinco estrelas 3/3 - 100%
- Quatro estrelas 0/3 - 0%
- Três estrelas 0/3 - 0%
- Duas estrelas 0/3 - 0%
- Uma estrela 0/3 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Tomáz, EEEP MANOEL MANO , Ceará - disse:
tomaz.cavalcante@hotmail.com19/07/2014
Cinco estrelasEstas são formas dos alunos aprenderem se divertindo, por isso, classifico como EXCELENTE!
-
maiquel vinicius gaitkoski rodrigues, accc , Rio Grande do Sul - disse:
tairine.dada@hotmail.com04/03/2012
Cinco estrelasmuito boa a explicacao a loteria e mais uma ilusao do povo brasileiro
-
Edilaine, CMEI MÁRIO DAVID ANDREAZZA , Rondônia - disse:
edilaineasnogueira@gmail.com09/07/2011
Cinco estrelasExcelente! Ser educador é ensinar a arte de contextualizar o saber.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus