12/01/2011
Rita Maria Cardoso Meirelles, Ivail Muniz Junior, Fernando Celso Villar Marinho, Jackson Lopes, Clayton Gonçalves Silva
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Tecnologia para a matemática |
| Ensino Fundamental Final | Matemática | Tratamento da informação |
| Ensino Médio | Matemática | Análise de dados e probabilidade |
| Educação de Jovens e Adultos - 2º ciclo | Matemática | Estatística, probabilidade e combinatória |
O que o aluno poderá aprender com esta aula
História e aplicabilidade da teoria das probabilidades.
Tabelas de dupla entrada.
Determinar a probabilidade de ganhos em um jogo.
Calcular a probabilidade da união, interseção e diferença de dois eventos.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Experimento aleatório
Evento e chances de um evento
Teoria dos conjuntos e operações de união, interseção e diferença de dois conjuntos
Gráfico de barras
Par ordenado
Representação de frações na forma percentual
Estratégias e recursos da aula
Converse um pouco com os alunos sobre a história da probabilidade e de suas diversas aplicações no cotidiano e em outras áreas de estudo.
Conte para a turma que o interesse do homem em estudar os fenômenos que envolviam determinadas possibilidades fez surgir a probabilidade. O surgimento da teoria das probabilidades teve início nos jogos de azar, comumente praticados através de apostas e disseminados na Idade Média.
Nota: Se achar oportuno fale também sobre os matemáticos que desenvolveram a teoria das probabilidades e, como fonte de informação, acesse o link: http://www.brasilescola.com/matematica/historia-probabilidade.htm.
Enumere algumas aplicações dessa teoria no cotidiano, tais como: avaliação de riscos e no comércio de matérias-primas, métodos de probabilidade na regulação ambiental, na teoria dos jogos etc.
Para mais exemplos, consulte o link: http://pt.wikipedia.org/wiki/Probabilidade.
Promova então uma discussão na turma e proponha que os alunos pesquisem sobre o assunto e tragam mais informações sobre as aplicações da Teoria das Probabilidades no cotidiano e em outras áreas de estudo.
Atividade 1:
Jogo da Cultura Popular
A atividade proposta permitirá que a turma vivencie a prática do jogo de habilidade conhecido popularmente como “Purrinha”.
Fonte: http://www.flickr.com/photos/diegorrrangel/4270405052/sizes/z/in/set-72157622941039210/
1. Proponha que o jogo seja feito em duplas.
2. Distribua três palitos (de fósforo ou similar) para cada aluno.
3. Providencie cópias do arquivo disponível no link: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/AtividadeJogandoPurrinha.pdf para distribuição aos alunos no momento da exploração da atividade.
4. Caso os alunos desconheçam as regras do jogo, enumere-as para os mesmos.
Regras do Jogo
1) Cada jogador, de posse dos três palitos, “esconde” em uma das mãos — sem que o outro jogador veja — uma das quantidades: 0 (nenhum palito), 1, 2 ou 3.
2) Em seguida, cada um aposta qual a soma de palitos que serão mostrados por eles.
3) Depois das apostas feitas, cada um abre a mão e mostra o número de palitos.
4) Vence o jogo aquele que acertar a soma obtida.
5. Dê início ao jogo, permitindo que os alunos “brinquem” por aproximadamente 10 minutos.
Exploração da Atividade
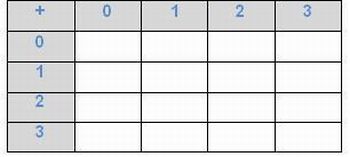
1. Após o período exploratório, entregue para os alunos a folha com a tabela de dupla entrada e solicite que eles a completem com as somas obtidas.
Imagem da autora.
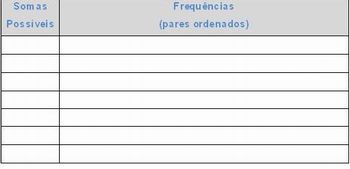
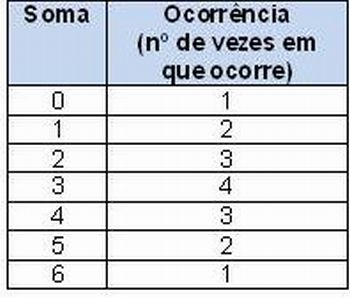
2. Peça então que os alunos preencham a segunda tabela constante na folha, com as somas possíveis e suas respectivas ocorrências, por exemplo, a soma 4 pode ocorrer em três situações: (2, 2), (3, 1) e (1, 3) onde a ordem dos pares é dada para diferenciar as quantidades de palitos de cada aluno (aluno1, aluno2).
Imagem da autora.
3. Após o preenchimento das tabelas, peça que os alunos respondam os seguintes questionamentos, registrando em seus cadernos, as respectivas respostas.
3.1. Quantas são as somas possíveis?
3.2. Quais são, respectivamente, a menor e a maior soma possível?
3.3. De quantas formas diferentes podem acontecer, respectivamente, a menor e a maior soma possível?
3.4. De quantas formas diferentes pode ocorrer:
3.4.1. soma igual a 2?
3.4.2. a sequência das somas 1, 2, 3, 4, 5 e 6?
3.4.3. soma menor que 3?
3.4.4. soma maior ou igual a 3?
4. Quantas somas diferentes podemos obter?
5. Em relação ao total de adições, qual a probabilidade de ocorrer as somas descritas nos itens 3.4.1, 3.4.2, 3.4.3 e 3.4.4?
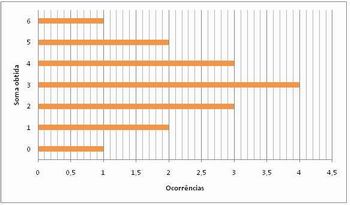
6. Represente, por meio de um gráfico de barras, a relação de cada soma com o número de sua ocorrência (frequência).
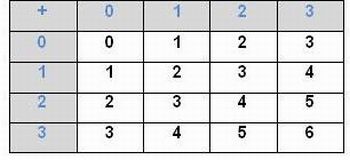
1.
Imagem da autora.
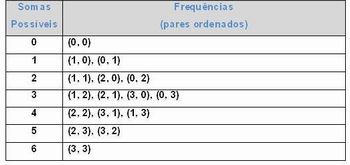
2.
Imagem da autora.
3.1. 7 somas possíveis
3.2. 0 e 6
3.3. Uma única forma possível nos dois casos.
Obtenção da menor soma possível: nenhum palito nas mãos de cada jogador: (0, 0)
Obtenção da maior soma possível: 3 palitos nas mãos de cada jogador: (3, 3)
Nota: Para melhor visualização da resolução dos itens a seguir, utilize o Data Show e exiba as imagens com as soluções.
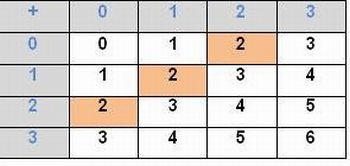
3.4.1. Três formas diferentes: (2, 0), (1, 1) e (0, 2)
Imagem da autora.
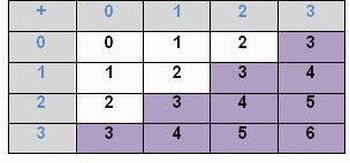
3.4.2. Duas formas diferentes:
1ª forma: (0, 1) → (0, 2) → (0, 3) → (1, 3) → (2, 3) → (3, 3)
2ª forma: (1, 0) → (1, 1) → (1, 2) → (1, 3) → (2, 3) → (3, 3)
Imagem da autora.
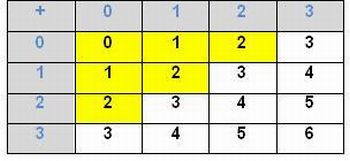
3.4.3. Seis formas diferentes: (0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (2, 0)
Imagem da autora.
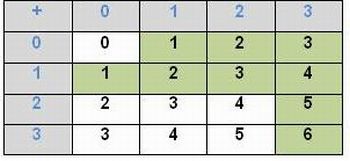
3.4.4. 10 formas diferentes: (0, 3), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 0), (3, 1), (3, 2), (3, 3)
Imagem da autora.
4. 16 maneiras diferentes
Obs: Caso haja necessidade, faça uma breve revisão sobre arredondamentos de números. Para revisão sobre o assunto acesse o link disponível nos recursos complementares.
5.
a) soma igual a 2: 3 em 16 ou 3/16 = 0,1875 ~ 19%
b) a sequência das somas 1, 2, 3, 4, 5 e 6: 2 em 16 ou 2/16 = 0,125 ~ 12%
c) soma menor que 3: 6 em 16 ou 6/16 = 0,375 ~ 38%
d) soma maior ou igual a 3: 10 em 16 ou 10/16 = 0,625 ~ 62%
6.
Imagem da autora.
Nota: Caso haja necessidade, reveja com a turma a construção de gráficos de barras.
Imagem da autora.
Nota:
Pode-se jogar com um número maior de alunos. Observar que a maior soma é sempre um múltiplo de 3 e que o número total de possibilidades de somas é uma potência de 2.
Atividade 2:
Rodas da Fortuna
Fonte: http://www.uff.br/cdme/rdf/rdf-html/rdf-c-br.html
Esta atividade oferece um aplicativo orientado para a simulação de experimentos aleatórios no computador, com ênfase em probabilidade geométrica. No caso, uma roda da fortuna, onde o espaço amostral e as probabilidades podem ser modificados, permitindo a simulação de experimentos clássicos como o lançamento de uma moeda (número de possibilidades = 2) e o lançamento de um dado (número de possibilidades = 6).
1. Para realização da atividade, encaminhe a turma ao laboratório de informática e peça que se acomodem em grupos de 3 alunos por computador
2. Informe-os de que a atividade a ser realizada é: Rodas da Fortuna – Parte I e, com auxílio do Data Show, exiba as imagens a seguir contando um pouco sobre “Fortuna e Sua Roda”.
Fonte: http://commons.wikimedia.org/wiki/File:Tadeusz_Kuntze_001.jpg
Fonte: http://en.wikipedia.org/wiki/File:ForutuneWheel.jpg
Fortuna (equivalente à deusa grega Tique) era a deusa da fortuna e a personificação da sorte na mitologia romana. Ela pode trazer boa ou má sorte, sendo algumas vezes representada com a vista vendada (como a moderna imagem da justiça) ou cega, pois distribuía seus desígnios aleatoriamente. Em outros quadros e desenhos, Fortuna é representada girando sua Roda da Fortuna (Rota Fortunae) de forma aleatória, mudando as posições das pessoas sobre a roda: algumas sofrem grande infortúnio, outras ganham lucros inesperados.
Fonte: http://www.uff.br/cdme/rdf/rdf-html/rdf-br.html
3. Solicite que acessem o link: http://www.uff.br/cdme/rdf/rdf-html/rdf-c-br.html e leia com os alunos os dois primeiros parágrafos das instruções. Após a leitura designe uma quantidade do número de possibilidades (2 a 13) para cada grupo, e permita então que eles, caso queiram, alterem as cores e os posicionamentos dos “nomes”.
Nota: Garanta que pelo menos um grupo fique com número de possibilidades igual a 2 e outro fique com número de possibilidades igual a 6.
4. Peça que os grupos iniciem então a atividade efetuando 20 sorteios!
5. Exiba, com o uso do Data Show, as imagens das atividades realizadas pelos grupos (uma por vez), solicitando que os “autores” de cada uma delas relatem as suas descobertas para os demais grupos.
Nota: Limite um tempo aproximado de 2 a 3 minutos para cada relato.
Enfatize a questão da probabilidade inicial de cada possibilidade e as frequências registradas após 20 lançamentos.
Exemplos:
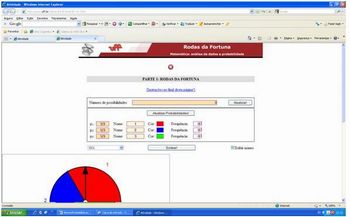
1) Simulando o lançamento de uma moeda e considerando 1: “cara” e 2: “coroa”, observa-se, neste sorteio feito por nós que, apesar de a probabilidade ser ½ para cada face em um único “lançamento”, após 20 deles, a ocorrência de cara foi 11 e de coroa foi 9.
Composição da autora.
Fonte: http://www.uff.br/cdme/rdf/rdf-html/rdf-c-br.html
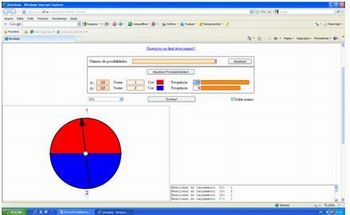
2) Simulando o lançamento de um dado e considerando 1, 2, 3, 4, 5, 6 as suas faces, observa-se, neste sorteio feito por nós que, apesar de a probabilidade ser 1/6 para cada face em um único “lançamento”, após 20 deles, as ocorrências das faces foram:
1 → 3
2 → 5
3 ou 5 → 2
4 ou 6 → 4
Composição da autora.
Fonte: http://www.uff.br/cdme/rdf/rdf-html/rdf-c-br.html
Atividade 3:
Probabilidade: Eventos Equiprováveis
Nessa atividade, você irá explorar as propriedades da união, interseção e diferença de eventos aleatórios e suas probabilidades a partir do experimento aleatório que consiste em sortear uma pessoa de um grupo formado por 28 meninos e meninas.
Professor, caso considere necessário, faça uma breve revisão sobre as operações de união, interseção e diferença de dois conjuntos.
Defina para os alunos:
Eventos equiprováveis são aqueles que têm a mesma chance de ocorrer.
Exemplo: Lançamento de uma moeda: 50% de chances de dar “cara” e 50% de dar “coroa”.
Pergunte aos alunos se os eventos das atividades 1 e 2 são equiprováveis.
Obs: Espera-se que os alunos percebam que os eventos da atividade 1 não são equiprováveis, pois as somas dos valores exibidos têm frequências diferentes.
1. Peça aos grupos, já organizados para realizarem a atividade anterior, que acessem o link: http://www.uff.br/cdme/prob-bonecos/prob-bonecos-html/prob-bonecos-start.html.
2. Leia, junto com a turma, as instruções contidas na página.
Fonte: http://www.uff.br/cdme/prob-bonecos/prob-bonecos-html/prob-bonecos-start.html
3. Permita que cada grupo faça a atividade uma única vez, até que a mesma seja realizada em sua totalidade com sucesso.
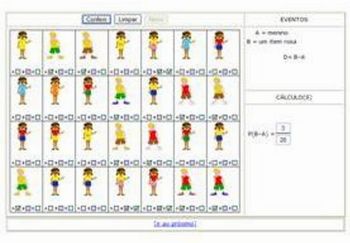
4. Após todos os grupos terem finalizado, peça para que cada um relate o seu experimento e mostre para os demais a solução encontrada.
Composição da autora.
Fonte: http://www.uff.br/cdme/prob-bonecos/prob-bonecos-html/prob-bonecos.html
Obs: Utilize a atividade como uma forma de avaliar os conhecimentos adquiridos.
Sugestão: Para enriquecimento da aula, sugerimos que você utilize o recurso do portal: Probabilidade com urnas, como atividade extra.
Fonte: http://objetoseducacionais2.mec.gov.br/bitstream/handle/mec/15600/open/file/index.html?sequence=279
Composição da autora.
Fonte: http://objetoseducacionais2.mec.gov.br/bitstream/handle/mec/15600/open/file/atividade1_parte1.html
Recursos Educacionais
| Nome | Tipo |
|---|---|
| Probabilidade com urnas | Animação/simulação |
Recursos Complementares
Algumas atividades apresentadas nessa aula, foram baseadas no livro TRATAMENTO DA INFORMAÇÃO: Explorando dados estatísticos e noções de probabilidade a partir das séries iniciais, do Projeto Fundão: Instituto de Matemática/UFRJ, coordenado pela Professora Maria Laura Mouzinho Leite Lopes. http://www.projetofundao.ufrj.br/matematica/images/stories/tratamento_da_informao_para_sries_iniciais.jpg
Arredondando Números: http://www.brasilescola.com/matematica/arredondando-numeros.htm
Fontes de pesquisa:
http://www.slideshare.net/MargarethDomingues/histria-das-probabilidades-e-eleies
http://revistagalileu.globo.com/Galileu/0,6993,ECT705269-2680,00.html
Avaliação
Avaliar a participação dos alunos durante as atividades desenvolvidas.
Avaliar a apresentação da pesquisa proposta no início dessa aula, em que os alunos mostrarão aplicações da Teoria das Probabilidades no cotidiano e em outras áreas de estudo.
Sem estrelas 0 classificações
- Cinco estrelas 0/0 - 0%
- Quatro estrelas 0/0 - 0%
- Três estrelas 0/0 - 0%
- Duas estrelas 0/0 - 0%
- Uma estrela 0/0 - 0%
Denuncie opiniões ou materiais indevidos!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus










 Probabilidade com urnas
Probabilidade com urnas