12/01/2011
Aparecida Clemilda Porto
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Educação de Jovens e Adultos - 2º ciclo | Matemática | Grandezas e medidas |
| Ensino Médio | Matemática | Geometria |
O que o aluno poderá aprender com esta aula
- Planificar o cone.
- Conceituar e identificar um setor circular.
- Identificar as formas geométricas que constituem o cone.
- Calcular a área das formas geométricas que constituem o cone.
- Definir a área lateral e total do cone.
- Calcular área lateral e total do cone.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
- Saber determinar a área do círculo.
- Saber calcular regra de três.
Estratégias e recursos da aula
Esta aula constará de 5 etapas de um estudo que poderá ser feito em duplas, em que o professor deverá orientaras atividades,fazendo interferências o mínimo possível. Ao final de cada etapa, ele deverá promover socialização do estudo entre os alunos, antes de seguir para a etapa seguinte.
Material: fichas de cartolina ou outro tipo de papel consistente.
1ª Etapa: FICHA 1
- Construa 3 círculos:
C1: com 4 cm de raio.
C2: com 7 cm de raio.
C3: com 5,5 cm de raio
2) Complete:
- A medida do ângulo que corresponde a uma volta completa do círculo é igual a_____________ graus.
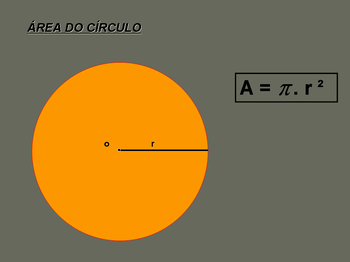
- Para calcularmos a área de um círculo fazemos o produto do (PI) pelo quadrado do raio do círculo.
Daí, temos então que a área do Círculo 1 é igual a __________________, a do Circulo 2 é igual a _______________ e a do círculo 3 é igual a_____________________.
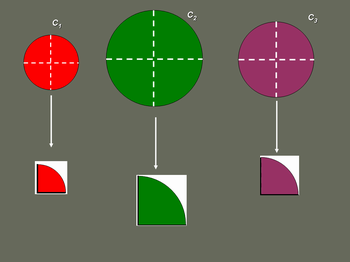
- Divida cada um dos três círculos em 4 partes iguais.
- Ao dividir o círculo, cada parte do círculo equivale a _____________ do círculo e a área de cada uma dessas partes será igual a ___________ da área do círculo. Portanto, a área dessa quarta parte do Círculo 1 é igual a _________, a do Circulo 2 é igual a ____________e a do Circulo 3 é igual a _________.
- O ângulo dessa parte do círculo mede_______________ graus.
- Divida, agora, os círculos em oito partes iguais.
- Cada parte do círculo assim dividido equivale a ________________ do círculo e a área de cada uma dessas partes será igual a ____________ do círculo. Portanto, a área dessa oitava parte do Círculo 1 é igual a _________, a do Círculo 2 é igual a __________e a do Círculo 3 é igual a _________.
- O ângulo dessa parte do círculo mede _____________ graus.
Observemos:
I) as quartas partes do círculo:
II) as oitavas partes do círculo.
A todas essas e outras partes de um círculo denominamos de SETOR CIRCULAR.
3) Escreva com suas palavras o Conceito de SETOR CIRCULAR:
_________________________________________________________________________________
_________________________________________________________________________________
2ª Etapa: FICHA 2
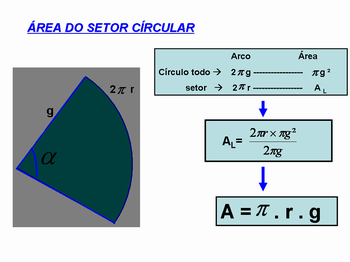
- Na etapa anterior, foi encontrada a área de cada setor circular. Dessa forma, percebemos que o setor circular é uma parte da região circular, ou seja, ele é uma fração da área do círculo. Assim, podemos afirmar que a área do setor circular depende da medida do ângulo central, o qual denominaremos de ângulo alfa (α), que, no caso, quando dividimos o círculo em 4 partes iguais temos que esse ângulo central mede _________graus. Quando dividimos em 8 partes iguais a medida do ângulo central é ________graus. Daí, temos que a área do setor circular é diretamente proporcional ao valor de α, pois a área de todo o círculo é diretamente proporcional a 360º.
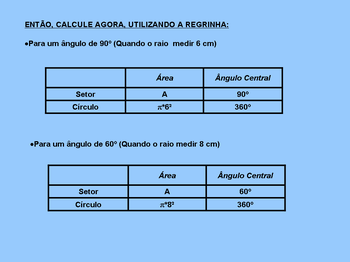
O cálculo da área de um setor circular pode ser realizado calculando-se a área total do círculo e depois se montando uma regra de três, em que a área total do círculo estará para 360°.
MODELO DA REGRA DE TRÊS SIMPLES
(Se houver necessidade, o professor poderá propor mais cálculos de área do setor utilizando a regrinha de três)
3ª Etapa: FICHA 3
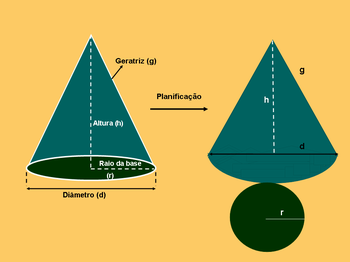
O professor entregará um cone para cada dupla. Sugere-se que o cone de cada dupla seja diferente dos demais cones. Nesse momento, o professor deve enfocar o que é a geratriz e mostrar a diferença entre raeio da base e a geratriz do cone.
- Planifique o cone. (Sugere-se que o cone tenha medidas plausíveis para que os alunos tenham facidade para calcular o que é proposto)
- O Cone planificado é formado por um _______________ e um ___________________ circular.
- O diâmetro do círculo que compõe sua base mede __________, logo o raio mede _________ e a área dessa base será de __________
- O ângulo central do setor circular mede __________ e o raio do círculo que deu origem ao setor, o qual denominamos geratriz, mede __________, dai, temos então que área do setor circular será igual a _______.
Retomando:
- A base do cone é formada pelo ______________, portanto a área da base (Ab) do cone é igual a _________
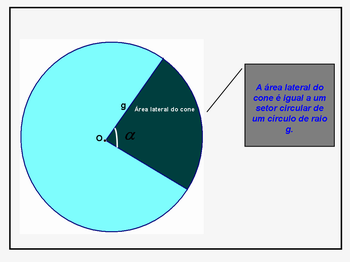
2) A parte lateral do cone é formado pelo _____________________, portanto a área lateral (AL) do cone é igual a _________.
3) Observe, no quadro abaixo, como calcular a área do setor circular (AL) sem a necessidade de se conhecer o ângulo do setor circular.
(Sugere que o professor tenha um quadro igual para que, se houver necessidade, ele possa dar uma assistência maior às duplas ou até mesmo para toda a turma)
4) Concluindo: Para calcularmos a área lateral do cone (AL) é nececessário conhecermos a medida do __________ e a medida da ____________________.
4ª Etapa: FICHA 4
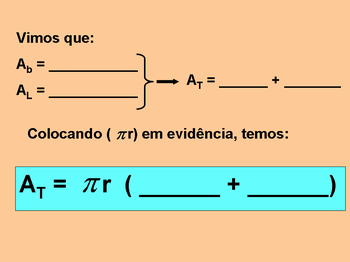
1) Ao planificarmos o cone na etapa anterior, vimos que este é composto pelo ______________________ que é sua base e pelo ____________________ que será sua superfície lateral.
2) A área total do cone, então, será determinada pela soma da______________________ com a ___________________
3) Volte ao cone que você planificou e calcule sua área, utilizando a fórmula que acabou de deduzir.
(Ao final dessa etapa, cada dupla deverá apresentar para o restante da turma como determinou a área total do seu cone.)
5ª etapa: FICHA 5
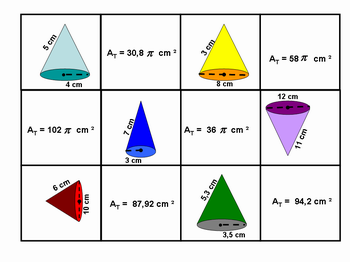
O professor entregara a 5ª ficha e pedirá às duplas que a recorte formando os pares de cone com a sua respectiva área .
Ao final cada dúpla apresentará um dos pares encontrados.
Exemplo de Ficha
_____________________________________________________________________________________________________
_______________________________________________________________________________________________________
Recursos Complementares
Para complementar as atividades, acesse:
http://www.youtube.com/watch?v=-CdYb1eAwRc
.Acessado em:13/12/2010
Avaliação
A avaliação será feita durante o desenvolvimento do estudo orientado por meio da participação dos alunos na discussão das questões propostas, para verificar se o aluno conseguiu demonstrar habilidades em identificar as formas geométricas que constituem o cone; identificar e conceituar um setor circular, identificar e calcular área lateral e total do cone.
Quatro estrelas 1 classificações
- Cinco estrelas 0/1 - 0%
- Quatro estrelas 1/1 - 100%
- Três estrelas 0/1 - 0%
- Duas estrelas 0/1 - 0%
- Uma estrela 0/1 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
vera soares santa helena, Colégio Estadual Rui Barbosa , Rio de Janeiro - disse:
vera.santahelena@gmail.com11/09/2012
Quatro estrelasMuito boa aula!!!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus