11/01/2011
Edson Luis Nunes, José Marcelo Gomes, Daniel Rodrigues Ventura.
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Educação de Jovens e Adultos - 2º ciclo | Ciências Naturais | Visões de mundo |
| Ensino Médio | Física | Equipamentos elétricos e telecomunicações |
O que o aluno poderá aprender com esta aula
· Entender a lei de Coulomb.
· Resolver exercícios envolvendo forças entre cargas elétricas pontuais.
· Caracterizar a força de interação entre cargas elétricas a partir da identificação da carga.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Leis de Newton, Lei da Atração Gravitacional, Carga Elétrica.
Estratégias e recursos da aula
Sugerimos inicialmente ao professor, lembrar aos alunos que quando duas cargas elétricas são aproximadas, se tiverem sinais contrários, elas se atraem e se tiverem mesmos sinais, elas se repelem, Princípio de Du Fay Surge então a dúvida: Qual o valor dessa força entre a interação das cargas? De que elas dependem?
A primeira análise quantitativa para responder a essas perguntas é creditada ao físico francês Charles Augustin de Coulomb (1736-1806) no ano de 1785.
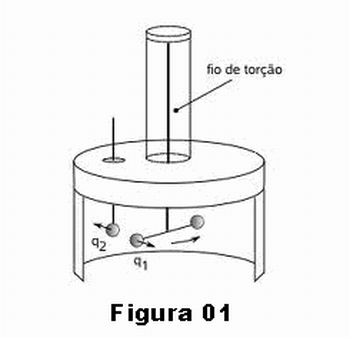
Coulomb desenvolveu uma balança de torção esquematizada na Figura 01 em que uma pequena esfera de carga q1 se encontra em equilíbrio numa barra tendo na outra extremidade outra esfera de mesma massa, sem carga elétrica. Outra pequena esfera de carga q2 é fixada na mesma horizontal próximo à carga q1. Surge então uma força de origem eletrostática entre as duas esferas carregadas com cargas q1 e q2. A barra é suspensa por um fio fino, de forma que as forças entre as cargas provocam um torque na barra forçando-a a girar. Por outro lado, ao girar, a barra provoca uma torção mecânica no fio que oferece certa força de resistência.
Com esse arranjo, Coulomb verificou que a força entre cargas elétricas, seja de atração ou de repulsão, é diretamente proporcional à carga de cada esfera e inversamente proporcional ao quadrado da distância entre elas.
http://www.mspc.eng.br/elemag/img01/eletr_balanca_torcao.png
Atividade I
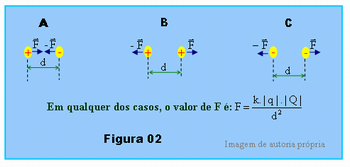
Uma carga elétrica é denominada de puntiforme ou pontual quando as dimensões do corpo que contém essa carga podem ser desprezadas. A Figura 02 esquematiza duas cargas pontuais bem próximas, isoladas da influência de outras cargas. Em A, as cargas têm sinais opostos, em B, ambas são positivas e em C, ambas são cargas negativas.
Em qualquer uma das três situações, a força de interação entre elas tem módulo F, tal que: F = k.|q|.|Q|/d2, nessa expressão, k é a constante eletrostática, constante da lei de Coulomb; o valor de k depende do meio onde se encontram as cargas, no vácuo k = 9.109 N.m2/C2, q e Q são as cargas que se interagem, a unidade de carga elétrica no SI é o Coulomb, abreviatura C; d é a distância entre as cargas.
O professor então poderá, usando a Figura 02, formular para a turma o seguinte exercício. Suponha que as cargas da Figura 02 estejam no vácuo e seus valores são q = 5.10-16C e Q = 20.10-16C. Sendo a distância entre elas de 2,0 mm, calcule o módulo da força de interação eletrostática entre as cargas q e Q.
Deverão resolver usando a expressão da lei de Coulomb.
- F = k.|q|.|Q|/d2
- F = 9.109.5.10-16.20.10-16/(2,0.10-3)2 (Unidades do SI, 2,0 mm = 2,0.10-3 m)
- F = 900.10-23/4,0.10-6
- F = 225.10-17 N
- F = 2,25.10-15 N
Atividade II
O professor deverá encaminhar a turma para um raciocínio que provavelmente tenha sido seguido por Coulomb, com a finalidade de concluir que a força elétrica seja proporcional ao produto das cargas e inversamente proporcional ao quadrado da distância entre elas. É bom salientar que, na época Coulomb, havia certa expectativa dessa relação, principalmente a relação do inverso do quadrado da distância, uma vez que já era conhecida a famosa expressão da atração gravitacional, em que a força entre dois corpos é proporcional ao produto da massa e inversamente proporcional ao quadrado da distância entre eles.
Para testar essa relação, Coulomb desenvolveu um dispositivo, em que determinava a carga de cada esfera e através da torção do fio calculava a força de interação entre elas.
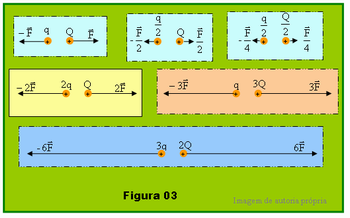
Suponha que os valores encontrados sejam como os dados representados nos esquemas da Figura 03. Observando cada quadro da figura iniciando pelo quadro superior à esquerda, pode ser constatado que:
- Para os valores das cargas q e Q, o módulo da força de interação entre elas é F.
- Mantendo a carga Q e reduzindo a carga q à metade, o módulo da força também fica reduzido à metade.
- Reduzindo as duas cargas à metade, o módulo da força de interação eletrostática entre elas fica reduzido à quarta parte.
- No quadro amarelo, a carga Q é mantida e dobra-se a carga q, nesse caso a força também duplicou.
- Triplicando o valor da carga Q mantendo o valor de q a força também triplica.
- Por fim foi duplicada a carga Q e triplicada a carga q, resultou que a força de interação entre as cargas tornou-se seis vezes maior.
O professor após expor a Figura 03 deverá perguntar para os alunos: O que se deve esperar da relação da força de interação eletrostática em função das cargas que se interagem?
Por influência da explanação anterior provavelmente vão concluir que a força é diretamente proporcional ao produto do valor das cargas. O professor deverá ponderar que essa é a resposta certa, mas para chegar corretamente a tais conclusões pela primeira vez, é preciso fazer um número muito maior de ensaios, sempre variando as grandezas envolvidas, os valores das cargas neste exemplo. O professor deverá ainda mostrar que para cada caso o quociente entre o módulo de F é diretamente proporcional ao produto dos módulos das cargas, se o produto dobra a força também dobra, se o produto triplica o módulo da força também triplica o que permite escrever: F/|q|.|Q| = (F/2)/(|q|/2).|Q| = (F/4)/[(|q|/2).(|Q|/2)] = 2F/(|2q|.|Q|) = 3F/(|q|.|3Q|) = 6F/(|3q|.|2Q|).
Resumindo, pode-se expressar que o módulo da força dividido pelo produto das cargas é constante, essa constante vamos chamar de k1. F/(|q|.|Q|) = k1.
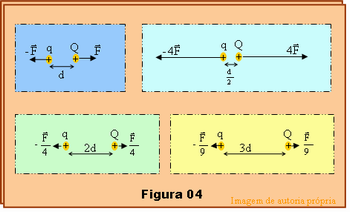
Depois o professor deverá apresentar a Figura 04 em outra fase de investigação da força eletrostática entre duas cargas pontuais em que as cargas das esferas foram mantidas constantes e a distância entre elas alterada. Observe pela figura que:
- Sendo d a distância entre as cargas, o módulo da força de interação eletrostática entre elas é F.
- Quando a distância d foi reduzida à metade, segundo quadro à direita superior da figura, o módulo da força entre as cargas quadruplicou.
- Numa segunda realização do experimento a distância d entre as cargas foi duplicada, 2d no esquema, quadro à esquerda inferior da figura, o módulo da força se reduziu a 1/4.
- Finalmente triplicando a distância d entre as cargas, último quadro da figura, verificou-se que o módulo da força de interação entre as cargas se tornou 9 vezes maior.
O professor então deverá novamente perguntar para a turma.
Embora o número de vezes em que a distância foi alterada seja pequeno, a partir dos dados obtidos, o que se pode concluir para a relação entre o módulo da força de interação e a distância d entre as cargas?
Apesar de ser pequeno o número de resultados obtidos como já argumentado no questionamento, existe certa lógica para afirmar que o módulo da força varia com o inverso do quadrado da distância entre as cargas. Provavelmente alguém da turma chegará a esta conclusão bastante lógica, mas caso ninguém se manifeste com esta resposta o professor deverá mostrar que em todos os casos houve a mesma proporção entre F e d2 indicando que F é inversamente proporcional ao quadrado de d; dobrando d, F fica reduzida de 22; triplicando d, F fica reduzida de 32, e assim por diante, de modo que: F.d2 = 4F.(d/2)2 = (F/4).(2d)2 = (F/9).(3d)2. Generalizando, F.d2 = constante, esta constante vamos chamar de k2; F.d2 = k2.
Depois o professor a fim de sugerir uma resposta conclusiva, a partir da proposição dos quadros da Figura 03 e da Figura 04 poderá dirigir aos alunos a seguinte pergunta que praticamente direciona a resposta:
Considere as expressões de F/|q|.|Q| = k1 e Fd2 = k2, ou seja, F = k1.|q|.|Q| e F = k2/d2, o módulo de F é diretamente proporcional ao produto do módulo das cargas e inversamente proporcional ao quadrado da distância entre elas. Como o módulo de F se relaciona com q, Q e d?
Parece obvio que os alunos concluirão o resultado unindo as duas expressões acima em uma única, obtendo a expressão equivalente a lei de Coulomb.
Se não chegarem a esse raciocínio, o professor deverá informar que partindo do enunciado da própria pergunta acima segue que o módulo de F é diretamente proporcional ao produto das cargas e também inversamente ao quadrado da distância entre elas, matematicamente expresso por, F = k.|q|.|Q|/d2, que é a própria expressão da lei de Coulomb; observe que a constante de proporcionalidade k é diferente de k1 e de k2, k é a constante da lei de Coulomb.
Atividade III
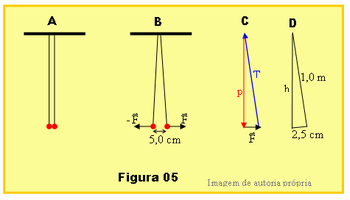
Depois que se tornou claro como Coulomb chegou à expressão da lei que leva seu nome, o professor ainda poderá usar o esquema da Figura 05 abaixo. Nessa figura duas minúsculas bolinhas metálicas estão penduradas por meio de fios inextensíveis e de massa desprezível. As bolinhas no Esquema A estão em equilíbrio de tal modo que se toca em um único ponto entre si. No esquema B elas foram carregadas encostando-se a elas um corpo condutor carregado eletricamente de modo que elas adquiriram cargas iguais. As bolinhas então se repelem e afastam-se de modo que a distância entre elas passa a ser de 5,0 cm.
Peça aos alunos para resolver o seguinte problema: calcule a carga q de cada bolinha sabendo que a massa de cada bolinha é 0,1 gramas e que o comprimento de cada fio é 1,0 metro. Use g = 10 m/s2.
O esquema C da Figura 05 corresponde ao diagrama de forças na bolinha da direita do esquema B e o esquema C ilustra as distâncias h, vertical da bolinha em B, o comprimento do fio e a distância deslocada para a direita devido à força de repulsão F, 2,5 cm a partir da vertical; o desenho está fora de escalas para melhor visualização didática. Os triângulos em C e em D são semelhantes, então, têm-se:
- F/p = 2,5 cm/h
0,1 grama = 10-4 kg e 1,0 m = 100 cm e aplicando o teorema de Pitágoras: (100)2 = h2 + (2,5)2; resulta daí que h = 99,9687 cm, pode-se então aproximar para 100 cm, logo,
- F/m.g = 2,5cm/100cm (Substituindo m e g), resulta em,
- F/10-4kg.10ms-2 = 0,025
- F/10-3 N = 0,025
- F = 0,025.10-3 N
- F = 2,5.10-5 N
Aplicando a lei de Coulomb.
- F = k.q.q/d2, (5 cm = 5.10-2 m).
- 2,5.10-5 = 9.109.q2/(5.10-2)2
- 2,5.10-5 = 9.109.q2/25.10-4
- 9.109q2 = 2,5.10-5.25.10-4
- q2 = 6,94.10-18
- q = 2,6.10-9 C ou q = 2,6 nC (1 nC = 1 nanoCoulomb = 10-9C )
Sugerimos que o professor assista ao seguinte vídeo que é bastante interessante e bem ilustrativo com excelente didática e sendo possível apresente o vídeo para os alunos. O vídeo é do Novo Telecurso – Ensino médio, e se encontra com o seguinte título e endereço abaixo.
Novo Telecurso - Ensino Médio - Física - Aula 37 (2 de 2): 8 min e 34 s
Recursos Complementares
Sugerimos ao professor que se ainda não viu o vídeo que mostra como Benjamin Franklin teve participação no processo que arquitetou a experiência de Charles Augustin Coulomb, acesse o seguinte vídeo que se encontra na internet, cujo título e endereço se encontram abaixo.
Força Elétrica - Lei de Coulomb: 6 min e 44 s
Avaliação
O professor poderá elaborar exercícios sobre aplicação da lei de Coulomb para que os alunos resolvam fora do horário de aulas, sugerimos o seguinte exercício:
- Calcule o módulo das forças gravitacional e eletrostática entre um próton e um elétron no átomo de hidrogênio. A distância entre um elétron e o próton em um átomo de hidrogênio é aproximadamente 5.10-11 m.
Módulo da carga do próton é igual ao módulo da carga do elétron = 1,6.10-19 C.
Massa do próton = 1,67.10-27 kg e massa do elétron = 9,1.10-31 kg.
A constante gravitacional é G = 6,67.10-11 N.m2/kg2 e a constante eletrostática da lei de Coulomb é k = 9.109 N.m2/C2.
Compare a intensidade entre as forças, gravitacional e elétrica, e tire suas conclusões.
Quatro estrelas 4 classificações
- Cinco estrelas 2/4 - 50%
- Quatro estrelas 2/4 - 50%
- Três estrelas 0/4 - 0%
- Duas estrelas 0/4 - 0%
- Uma estrela 0/4 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Rojuhercymar Boreli, Eu mesma , Minas Gerais - disse:
roje.boreli@hotmail.com28/03/2016
Quatro estrelasMuito boa anotação pedagógica. Valeu!
-
sielly sousa, c.e salomão cury rad , Maranhão - disse:
sielly-hta-15@hotmail.com16/04/2013
Cinco estrelasotimo,maravilha adorei essa aula e aprendi bastante.
-
Bethania, UFPB , Paraíba - disse:
bethania_pontes@hotmail.com06/10/2011
Quatro estrelasÓtima a aula, tirrou grande parte de minhas duvidas.
-
NEUZA, EE.ORLANDINE , Rio de Janeiro - disse:
neuza.carlos@gmail.com01/07/2011
Cinco estrelasAdorei a colocação sobre a materia e a ilustração.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus