25/01/2011
Rita Maria Cardoso Meirelles, Ivail Muniz Junior; Fernando Celso Villar Marinho, Jackson Lopes, Clayton Gonçalves Silva, Raquel Cupolillo Simões de Sousa
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Números e operações |
O que o aluno poderá aprender com esta aula
- Entender o conceito de capitais equivalentes.
- Trabalhar com os conceitos de valor presente e valor futuro;
- Entender o conceito de data focal;
- Calcular o valor nominal conhecido o atual e vice-versa;
- Entender quanto custa de verdade um bem adquirido a prazo.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
- Porcentagem;
- Fator de atualização. (É importante que o aluno soubesse que um capital C, aumentado de uma taxa i, fica multiplicado por (1+i). Veja a aula: O valor do dinheiro no tempo, nesse portal.
- Progressão geométrica.
Estratégias e recursos da aula
Prezado professor.
Dois capitais são equivalentes quando são iguais se comparados em uma mesma data. Assim, se João aplica 100 reais a uma taxa de juros de 5% ao mês, 100 reais hoje e 105 reais daqui a 1 mês são equivalentes, ou seja, ter 100 hoje e 105 daqui a 1 mês lhe é indiferente. Isso vale para muitas situações. Uma dívida de 1000 reais hoje, a uma taxa de juros de 20% ao bimestre, e OUTRA de 1200 daqui a 2 meses, também são equivalentes, pois a primeira transformar-se-á na segunda após 2 meses.
Esse conceito nos remete a um dos princípios básicos em Matemática Financeira:
- Quantias só podem ser somadas se estiverem na mesma época (mesma data);
- Quantias só podem ser comparadas se estiverem na mesma época;
Isso é importante, pois, achar que 100 reais valem menos que 110 reais pode ser um engano, pois se aplicarmos 100 à taxa de 1% ao mês, após 12 meses, teremos R$ 112,68 o que é maior que 110, se este estiver referido à mesma data. Então 100 é maior que 110, referidos às datas mencionadas, nas condições dadas.
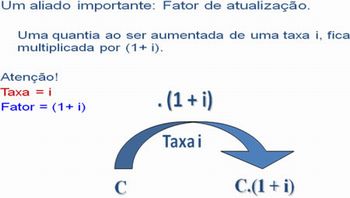
A grande maioria das análises de situações financeiras utiliza esse conceito. Quando calculamos quanto vale uma quantia em outra época, estamos transportando o dinheiro no tempo. Para fazer isso, basta lembrar que quando um valor aumenta de uma taxa i, ele fica multiplicado pelo fator (1 + i) e quando diminui de uma taxa i ele fica dividido por (1+ i). O esquema abaixo ilustra isso muito bem.
Consequentemente, para avançar n períodos basta multiplicar por (1 + i)n; para voltar n períodos, basta dividir por (1 + i)n.
Não esqueça de consultar a aula: “O VALOR DO DINHEIRO NO TEMPO”, disponível nesse portal.
ATIVIDADE 1.
Nessa atividade veremos como utilizar o conceito de capitais equivalentes para analisar situações financeiras comuns no Brasil.
1) Peça aos alunos, com pelo menos 2 semanas de antecedência, que pesquisem e tragam para essa aula encartes, anúncios, folder, jornais, revistas etc., com preços de produtos há 10 anos atrás. Se sua cidade sofreu um boom imobiliário na última década, peça também para descobrirem quanto custava um determinado imóvel há 10 anos e quanto custa agora. Se for novo, veja o preço de um equivalente.
2) Comece a aula pedindo aos alunos para apresentarem os produtos que sofreram as maiores variações dentre os pesquisados.
3) Encerre essa introdução reforçando que o dinheiro não é estático. Ele varia com o tempo. Tempo e dinheiro são conceitos inseparáveis. Toda quantia deve estar REFERIDA A UMA ÉPOCA, UMA DATA!
4) Apresente a situação abaixo e peça para os alunos analisarem.
5) Situação I – O que é melhor: Receber 1.000 reais hoje ou 3.000 reais daqui a 10 anos?
6) Situação II – O que é melhor do ponto de vista financeiro: investir na compra de um apartamento hoje por R$ 200.000,00, que tem uma valorização estimada de 100% em 6 anos ou pegar esse dinheiro e aplicar a juros de 1% ao mês, durante esse mesmo período? Depois dos cálculos amplie a discussão analisando a expressão “valorização estimada”.
Aqui o professor pode sugerir que os alunos pesquisem sobre a valorização imobiliária na região onde vivem, e utilizem esses dados para apoiar ou refutar a estimativa apresentada no problema. Peça inclusive para refazerem os cálculos com os novos dados obtidos.
7) Situação III – Comprar uma televisão de 4.000 reais hoje, em 10 vezes sem juros, ou comprar à vista com 10% de desconto? E se o desconto fosse de 15%? Considere que a taxa disponível de investimento para o comprador seja de 2% ao mês.
Deixe os alunos por 30 minutos discutindo essas questões. Após esse tempo de investigação analise cada situação com eles, utilizando o conceito de capitais equivalentes.
| SITUAÇÃO I |
| CAPITAL INICIAL |
1.000 |
| TEMPO |
120 |
| CAPITAL FINAL |
3.000 |
| TAXA |
0,92% |
Imagem do autor.
| CONCLUSÃO |
| ESSE INVESTIMENTO TEM RENTABILIDADE DE 0,92% SE A PESSOA TEM UMA TAXA MAIOR, É MELHOR RECEBER AGORA. SE A TAXA É MENOR, É MELHOR RECEBER DAQUI A 10 ANOS A ANÁLISE AQUI É ESTRITAMENTE FINANCEIRA! |
Imagem do autor.
O aluno também pode partir de uma taxa pesquisada, como a poupança ou um fundo de renda fixa e, a partir daí, trazer os valores para a mesma época, concluindo para àquela taxa qual a melhor opção.
| SITUAÇÃO II |
| CAPITAL INICIAL |
R$ 200.000,00 |
| TEMPO |
72 |
| TAXA |
1,00% |
| CAPITAL FINAL |
R$ 409.419,86 |
Imagem do autor.
TAXA 104,71%
| CONCLUSÃO |
| APLICANDO O DINHEIRO A 1% AO Mês, tem um valor Futuro maior que o previsto pela valorização do apartamento. Pode-se alternativamente calcular a taxa equivalente para o período de 6 anos Essa taxa é 1,01^72 -1 = 104,71%, maior que os 100% previstos |
Imagem do autor.
| SITUAÇÃO III |
Primeiro, é preciso reforçar que a taxa de investimento para o comprador é 2% ao mês. Vamos descobrir os valores presentes de cada prestação.
| VALOR DE TABELA |
4000 |
| NÚMERO DE PRESTAÇÕES |
10 |
| TAXA DE ATRATIVIDADE |
2% |
Imagem do autor.
VAMOS TRAZER TODOS OS VALORES PARA A DATA ZERO. ESSA DATA É CHAMADA DATA FOCAL.
| TEMPO |
VALOR DA PARCELA |
VALOR ATUAL |
| 0 |
R$ 0,00 |
R$ 0,00 |
| 1 |
R$ 400,00 |
R$ 392,16 |
| 2 |
R$ 400,00 |
R$ 384,47 |
| 3 |
R$ 400,00 |
R$ 376,93 |
| 4 |
R$ 400,00 |
R$ 369,54 |
| 5 |
R$ 400,00 |
R$ 362,29 |
| 6 |
R$ 400,00 |
R$ 355,19 |
| 7 |
R$ 400,00 |
R$ 348,22 |
| 8 |
R$ 400,00 |
R$ 341,40 |
| 9 |
R$ 400,00 |
R$ 334,70 |
| 10 |
R$ 400,00 |
R$ 328,14 |
Imagem do autor.
| TOTAL NA ÉPOCA ZERO |
3593,03 |
|
| DESCONTO DE 10% |
3600,00 |
MELHOR COMPRAR A PRAZO |
| DESCONTO DE 15% |
3400,00 |
MELHOR COMPRAR À VISTA |
Imagem do autor.
Na planilha disponível em: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/planilhas_equivalencia_capitais.xls o aluno poderá simular taxas, valores e número de prestações. O professor pode, assim, criar várias situações a partir desses dados.
Há uma outra maneira de se obter o valor de R$ 3.593,03, utilizando a soma da P.G. Para maiores detalhes de como utilizar tal procedimento, veja a aula SÉRIES UNIFORMES, disponível nesse portal.
ATIVIDADE 2.
Nessa atividade lidaremos com investimentos sucessivos e metas de rentabilidade a médio prazo. O caso a ser analisado está intimamente ligado ao planejamento financeiro do dinheiro reservado para poupança, tanto de micro-empresas, quanto das famílias brasileiras. Utilizaremos planilhas eletrônicas para ampliar a análise do caso estudado e incentivar a comunicação de ideias por meio dessa ferramenta.
1) Inicialmente, divida a turma em grupos;
2) Diga aos alunos que dentro do planejamento financeiro familiar ou de uma pequena empresa, parte da renda deve ser poupada, sempre que possível. E onde poupar? Reforce que apesar de a poupança ser o investimento mais utilizado no Brasil, por ser mais conhecido, por não pagar Imposto de Renda e ser de fácil aplicação, há outras oportunidades de investimento. Decidir entre investimentos requer, em muitos casos, conhecimentos de Matemática Financeira, dentre eles o de capitais equivalentes.
3) Apresente aos alunos um pequeno Estudo de Caso abaixo.
O CASO DA EMPRESA IMJ CONSULTORIA.
Uma empresa aplica R$ 250.000,00 em um investimento que proporciona juros de 1% a.m., durante 6 meses. Depois dos 6 meses, há uma perspectiva de oferta de um investimento com rentabilidade de 4% ao bimestre. A empresa pensa em aplicar o montante da aplicação anterior por mais 6 meses nesse novo investimento. O FERNANBANK oferece uma segunda alternativa. Deixar o dinheiro aplicado a uma taxa de juros de 1,5% ao mês, durante um ano, sem poder retirar o dinheiro nesse período.
A empresa deseja saber qual é o melhor investimento, do ponto de vista financeiro.
Responda às perguntas abaixo e decida qual é a melhor opção de investimento, tomando como apoio o conceito de capitais equivalentes.
a) Qual o montante após 6 meses aplicando na primeira opção?
b) Reaplicando esse valor ano na taxa prevista, qual o montante nessa segunda operação?
c) Qual a taxa de juros anuais dessa dupla operação?
d) Qual a taxa de juros anuais da operação proposta pelo FERNANBANK?
e) Qual a melhor opção de investimento?
f) Qual a rentabilidade, em reais, dessa melhor operação?
g) Faça um relatório para apresentar suas conclusões, que inclua uma planilha no Excel com a evolução mês a mês do capital investido, em cada uma das opções de investimento.
O aluno deverá apresentar planilhas semelhantes às que seguem abaixo.
| INVESTIMENTO A |
| TEMPO |
JUROS VALOR |
ATUAL |
| 0 |
0,00 |
250.000,00 |
| 1 |
2.500,00 |
252.500,00 |
| 2 |
2.525,00 |
255.025,00 |
| 3 |
2.550,25 |
250.000,00 |
| 4 |
2.575,75 |
257.575,25 |
| 5 |
2.601,51 |
260.151,00 |
| 6 |
2.627,53 |
262.752,51 |
| 7 |
5.255,56 |
265.380,04 |
| 8 |
5.359,64 |
270.635,60 |
| 9 |
5.465,78 |
275.995,24 |
| 10 |
5.574,03 |
281.461,02 |
| 11 |
5.684,41 |
292.719,46 |
| 12 |
5.796,99 |
298.516,45 |
Imagem do autor.
| TAXA ANUAL |
19,41% |
| RENTABILIDADE EM R$ |
48.516,45 |
Imagem do autor.
| INVESTIMENTO B |
| TEMPO |
JUROS |
VALOR ATUAL |
| 0 |
0,00 |
250.000,00 |
| 1 |
3.750,00 |
253.750,00 |
| 2 |
3.806,25 |
257.556,25 |
| 3 |
3.863,34 |
261.419,59 |
| 4 |
3.921,29 |
265.340,89 |
| 5 |
3.980,11 |
269.321,00 |
| 6 |
4.039,82 |
273.360,82 |
| 7 |
4.100,41 |
277.461,23 |
| 8 |
4.161,92 |
281.623,15 |
| 9 |
4.224,35 |
285.847,49 |
| 10 |
4.287,71 |
290.135,21 |
| 11 |
4.352,03 |
294.487,23 |
| 12 |
4.417,31 |
298.904,54 |
Imagem do autor.
| TAXA ANUAL |
19,56% |
| RENTABILIDADE EM R$ |
48.904,54 |
Imagem do autor.
O melhor investimento é o B.
ATIVIDADE 3.
Nessa atividade vamos trabalhar com aumentos salariais, capitais equivalentes e aumento do poder de compra e captação na poupança.
1) Peça aos alunos para acessarem a matéria abaixo, ou se isso não for possível, podem apenas ler as informações abaixo.
Disponível em http://g1.globo.com/economia-e-negocios/noticia/2010/12/caderneta-de-poupanca-capta-r-4-bilhoes-em-novembro.html
Acessado em 06 de Dezembro de 2010.
2) Inicie uma discussão sobre porque a Poupança tem tantos investidores.
3) Qual a rentabilidade da poupança em Novembro de 2010?
4) Se uma pessoa aplicou R$ 10.000,00 na poupança, quanto terá após 12 meses, considerando uma rentabilidade de 0,6% ao mês?
5) Se a inflação desse período de 12 meses foi de 5%, o dinheiro aplicado teve ganho real? De quantos por cento?
6) E se a inflação fosse de 6%, teria ganho real?
7) Qual a inflação estimada para 2010? Considerando a inflação anual prevista para 2010 e a rentabilidade da poupança no mesmo período, quem aplicou na poupança em 2010, terá algum tipo de ganho real ou terá apenas o seu dinheiro corrigido, ou seja, apenas garantirá que ele não se desvalorizou?
Nessa questão o aluno precisará pesquisar as taxas de inflação e da poupança para 2010. Tais dados podem ser obtidos em: http://www.portalbrasil.net
8) Termine a aula propondo mais um problema relacionado aos assuntos abordados na atividade.
Recursos Complementares
Uma aula única de Matemática Financeira do Professor Augusto C. de O. Morgado, está disponível em http://video.impa.br/index.php?page=janeiro-de-2007. NÃO DEIXE DE ASSISTIR!!!
Avaliação
- Avaliação individual. Aplicar problemas e situações em que o aluno mostre como utilizar os conceitos apresentados para atacar e resolver situações financeiras.
- Avaliação coletiva. Resolução de problemas que requeiram pesquisa de informações na Internet, como as apresentadas nas atividades. O estudo de caso é uma ferramenta de avaliação interessante, mas recomendamos que sempre esteja associada à produção textual também. Cálculos são indispensáveis, mas não devem ser suficientes!!!
Cinco estrelas 1 classificações
- Cinco estrelas 1/1 - 100%
- Quatro estrelas 0/1 - 0%
- Três estrelas 0/1 - 0%
- Duas estrelas 0/1 - 0%
- Uma estrela 0/1 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Rodrigo Correia Muniz, EE Teófilo Paulino , Espírito Santo - disse:
correiamuniz@yahoo.com.br22/08/2013
Cinco estrelasAchei a condução dos termos teóricos às situações práticas tão palpáveis incrível. Sem dúvida é o tipo de aula que acrescenta aos alunos.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus