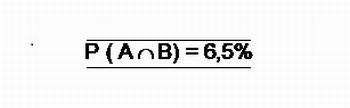12/01/2011
Rita Maria Cardoso Meirelles, Ivail Muniz Junior, Fernando Celso Villar Marinho, Jackson Lopes, Clayton Gonçalves Silva
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Tecnologia para a matemática |
| Ensino Médio | Matemática | Análise de dados e probabilidade |
| Educação de Jovens e Adultos - 2º ciclo | Matemática | Estatística, probabilidade e combinatória |
| Ensino Médio | Matemática | Geometria |
O que o aluno poderá aprender com esta aula
Cálculo das probabilidades relacionadas às áreas de figuras planas.
Aplicar probabilidade condicional na resolução de problemas.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Experimento aleatório, espaço amostral e evento.
Cálculo da probabilidade de um evento.
Probabilidade da união e interseção de dois eventos.
Representação de frações na forma percentual.
Área de figuras planas.
Teoria dos conjuntos.
Estratégias e recursos da aula
Professor, inicie a aula conversando com a turma sobre esportes radicais. Pergunte se os alunos sabem o que são esportes radicais e, caso não saibam, comente que são esportes não-formais, cuja principal característica é fugir do trivial; ou seja, escapar dos esportes convencionais, coletivos ou individuais, praticados, por exemplo, com bolas em quadras ou campos.
Imagem editada pela autora a partir de
http://visaocarioca.com.br/wp-content/uploads/2008/11/asa.jpg
http://www.imotion.com.br/imagens/data/media/77/8787paraquedas.jpg
http://www.mapa-mundi.com/img/fotos/noticias/2006/07/24/1241043142.jpg
http://t3.gstatic.com/images?q=tbn:ANd9GcQp-FwWBtEKw3zNZlHv9cLmHC28jUlGOg6wOusFSsM1_n8wqTN7
Fale também que uma condição quase essencial é o contato com ambientes naturais como praias, bosques, florestas e montanhas, cachoeiras, rios e até mesmo no ar. Existem também ambientes arquitetônicos adaptados à prática: urbanidade das ruas, praças, escadarias, corrimões etc.
Solicite que os alunos façam uma pesquisa sobre tais esportes, classificando-os e verificando como ocorrem as competições. As atividades a seguir, foram baseadas em esportes radicais realizados no ar.
Nota: Para mais referências sobre o assunto veja os Recursos Coplementares.
Obs: Para realização das atividades 1, 2 e 3 acesse o link: http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/MalhaQuad.pdf, tire cópias e distribua um exemplar para cada aluno.
Atividade 1:
A decolagem no voo de Asa-Delta
Esta atividade tem como objetivo a compreensão do cálculo da probabilidade de um evento através de uma abordagem geométrica.
Imagem da autora
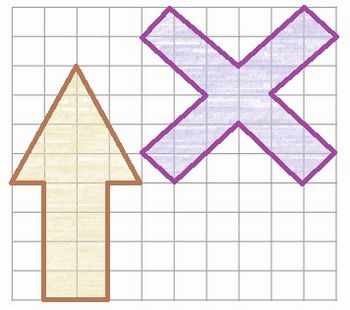
Informe aos alunos que nas competições de asa-delta o tempo de decolagem, ou de largada, pode ser definido pelo método conhecido como Starting Gate. Neste método, os pilotos decolam e ficam aguardando no ar a abertura do portão de largada. Este portão é definido por uma grande faixa colocada no chão. Enquanto a faixa estiver simbolizando um "X" o portão está fechado. Quando este "X" vira uma "seta", significa que o portão está aberto. Os pilotos deverão então passar sobre o portão e partir para o voo.
1. Solicite que os alunos realizem as etapas descritas abaixo:
1.1. Desenhe dois polígonos representando o X e a seta na malha quadriculada e pinte a região interna de ambos. Os polígonos não devem possuir pontos em comum.
1.2. Determine a área de cada polígono.
Nota: Considere cada quadrícula como uma unidade de área.
1.3. Encontre as razões entre a área de cada um dos polígonos criados e a área total da malha quadriculada.
1.4. De acordo com os polígonos desenhados, qual símbolo o atleta visualizará melhor?
2. Estabeleça um tempo para os alunos refletirem e desenvolverem as questões.
3. Após este tempo, corrija a atividade no quadro de giz, estabelecendo um momento de troca de ideias entre você e os alunos.
1. Um exemplo de solução:
1.1.
Imagem da autora
1.2.
- Polígono que representa a seta: 16 unidades de área
- Polígono que representa o X: 18 unidades de área
1.3.
- Razão entre a área do polígono que representa a seta e a área total: 16/100 = 16%
- Razão entre a área do polígono que representa o X e a área total: 18/100 = 18%;
1.4. O atleta visualizará melhor o símbolo que possuir o maior número de quadrículas pintadas em relação à malha, isto é, o símbolo que possuir maior probabilidade. Neste exemplo será o X.
A turma deve perceber que as razões obtidas são as probabilidades de serem selecionadas, segundo a figura formada, quadrículas da cor marrom e da cor roxa.
Atividade 2:
O pouso na mosca
O objetivo é fazer com que o aluno perceba a utilização do conceito da probabilidade da interseção de dois eventos.
Ressalte que nas competições de paraquedismo a modalidade mais antiga é a de precisão. Consiste em pular com o velame (nome da lona do paraquedas) aberto, objetivando atingir um alvo no chão, chamado de mosca. Considere que o paraquedista está realizando o pouso num campo representado pela malha quadriculada.
Fonte: http://www.culturamix.com/wp-content/uploads/2010/08/Modali-2.jpg
1. Peça a turma para realizar as etapas abaixo:
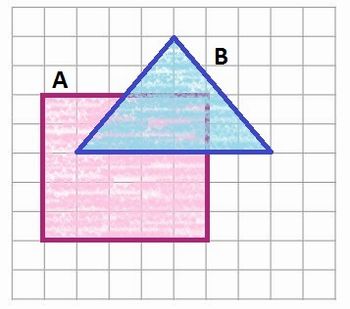
1.1. Construa um alvo com dois polígonos de forma que haja uma interseção entre os polígonos. Denomine uma região de A e a outra de B.
Notas:
a) A turma deve perceber que existem dois eventos:
- O paraquedista cair na região A
- O paraquedista cair na região B
b) A malha que representa o campo é o espaço amostral. Chame-o de E.
1.2. Qual a probabilidade de o paraquedista aterrisar na região A? E na região B?
1.3. Qual a probabilidade de o pouso ser realizado nas duas regiões ao mesmo tempo?
1.4. Represente a situação descrita no item anterior (1.3) simbolicamente.
2. Reserve um espaço na aula para os alunos trabalharem estes tópicos.
3. Ao término do tempo estabelecido, como na atividade 1, verifique com a turma o desenvolvimento de cada item utilizando o quadro de giz.
1. Um exemplo de solução:
1.1.
1.2. A probabilidade do pouso ser realizado na região A é de 25% e na B é de 12%.
1.3. A probabilidade do paraquedista pousar nas duas regiões ao mesmo tempo é de 6,5%.
1.4.
Imagem da autora
Atividade 3:
O objetivo da atividade é introduzir o cálculo da probabilidade condicional de dois eventos.
Os balonistas e o arremesso da fita
Fonte: http://t0.gstatic.com/images?q=tbn:ANd9GcT01y56pCK-Cm_p9BtS0t-Pdj6sGv4aF2Ktf66abCMfve4iS57crA
Enfatize que, apesar de não parecer, o balonismo também é um esporte radical e que dentro das suas modalidades de competição existe o Fly In, onde os pilotos devem jogar uma fita em um alvo estrategicamente escolhido, depois de decolar a uma distância de, no mínimo, 3 km.
1. Solicite que os alunos realizem as etapas a seguir:
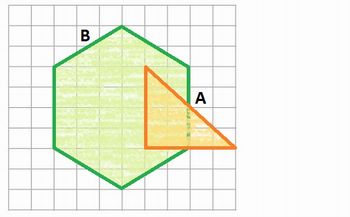
1.1. Construa um alvo com dois polígonos de tamanhos diferentes, de forma que haja uma interseção entre os mesmos. Chame a região menor de A e a maior de B.
1.2. Considerando a a malha quadriculada como espaço amostral, qual é a probabilidade de a fita cair em A?
1.3. Considere agora que, ao arremessar a fita "o praticante percebeu que a mesma caiu na região maior (B)". Analisando a malha quadriculada, defina se o espaço amostral se altera e determine-o caso ocorra tal alteração.
Nota: A turma deve perceber analisando a malha quadriculada, que o espaço amostral diminuiu, ficando restrito à região B.
1.4. Sabendo que a fita caiu em B, considere a possibilidade desta fita cair exatamente em A. Chame este evento de C. O que significa este evento?
1.5. Qual é a probabilidade do evento C?
Nota: A turma deve perceber que a probabilidade do evento "a fita cair na região A" foi alterada pela presença do evento "o praticante percebeu que a fita caiu na região B".
2. Permita aos alunos um momento para análise e desenvolvimento da situação proposta.
3. Estabeleça a troca de ideias com a turma para verificar o desenvolvimento de cada item utilizando o quadro de giz.
1. Um exemplo:
1.1.
Imagem da autora
1.2. A probabilidade de a fita cair na região A é de 8%.
1.3. O espaço amostral se altera passando a ser apenas a região B.
1.4. O evento C significa que a fita deve cair ao mesmo tempo em B e em A e que é a interseção das duas regiões.
1.5. A probabilidade do evento C, interseção dos eventos A e B, é aproximadamente 0,17%.
Informe à turma que este último resultado representa a probabilidade de a fita cair na região A, condicionada ao fato de ela ter caído em B.
Atividade 4:
Definindo Probabilidade Condicional
Professor, utilize o encadeamento do raciocínio desenvolvido na atividade 3 para chegar à definição.
Faça a construção do resultado junto com a turma no quadro de giz.
Peça aos alunos para registrarem em seu cadernos.
Notação: P (A/B)
Lê-se: Probabilidade condicional de ocorrer A, tendo ocorrido B.
Assim, utilizando a definição de probabilidade, podemos notar que
Imagem da autora
Curiosidade:
Os dardos também já foram considerados esportes radicais, porém isto ocorreu na época de Henrique VIII da Inglaterra e Carlos VI da França, que eram ávidos entusiastas destes jogos originários das lutas e competições de arqueiros.
Mais informações se encontram no link : http://www.portalsaofrancisco.com.br/alfa/dardos/historia-do-jogo-de-dardos.php#
Atividade 5:
Lançamento de dardos e probabilidade geométrica
O objetivo desta atividade é mostrar que os alunos são capazes de calcular a probabilidade pedida utilizando basicamente a intuição.
1. Leia o problema com a turma.
Um dos alunos de uma turma, desejava mostrar para seus colegas que possuia um ótimo senso de direção. Logo, propôs o desafio de, com os olhos vendados, procurar atingir um alvo circular com 50 cm de raio, tendo no centro um disco de 10 cm de raio. Em certo momento temos a informação de que ele acertou o alvo.
Fonte: http://www.jogueaki.ig.com.br/img/thumbs/501darts.gif
2. Proponha as atividades:
a) Encontre a área do alvo.
b) Calcule a área da região central do alvo.
c) Qual a probabilidade de que o aluno tenha atingido o disco central?
Nota: Reserve um momento para a discussão do problema. Em seguida, corrija no quadro de giz, com a participação de todos, verificando as soluções encontradas.
Obs: Esta atividade foi adaptada de http://portal.mec.gov.br/seb/arquivos/pdf/EnsMed/expensmat_3_4e5.pdf
a) A área do alvo é 2.500 pi unidades de área.
b) A área da região central do alvo é 100 pi unidades de área.
c) A probabilidade é 0,04 ou 4%.
Atividade 6:
Manipulando e interagindo com o software Nippe Descartes para solidificar o conceito de probabilidade condicional
Nesta atividade será utilizado o software Nippe Descartes. As informações sobre este software encontram-se nos Recursos Complementares.
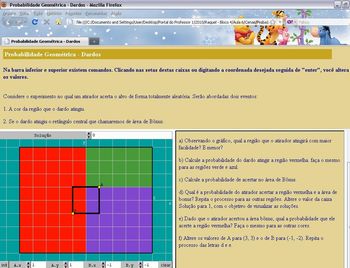
Informe aos alunos que a atividade a ser realizada no laboratório de Informática, tem como objetivo a solidificação do entendimento de como pode ser calculada a probabilidade condicional através de uma visão geométrica.
Peça a turma que acessem o link http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/Proba1.html e iniciem a atividade.
Imagem da autora
a) O atirador atingirá com maior facilidade a região vermelha e com menor a verde.
b) A probabilidade do dardo atingir a região vermelha é de 50%, a verde é de 18,75% e a azul é de 31,25%.
c) A probabilidade do atirador acertar a área de bônus é de 5%.
d) Solução na cena.
e) Chamando a região vermelha de V, a verde de D, a azul de A e a área de bônus de B, temos:
- P (V / B) = 50%
- P (D/B ) = 0
- P (A / B) = 50%
f) Resposta na cena.
Recursos Complementares
Fontes de Pesquisa:
1. Probabilidade Geométrica
http://objetoseducacionais2.mec.gov.br/handle/mec/15585
http://redeabe.org.br/oficina_probabilidade_geometria.pdf
http://www.ipef.br/publicacoes/scientia/nr37/cap09.pdf
2. Esportes radicais
http://www.educacionalpositivo.com.br/educacao_fisica/alunos/alunos16.asp
http://360graus.terra.com.br/asadelta/default.asp?did=652&action=dica
http://www.culturamix.com/saude/esporte/radical/modalidades-de-paraquedismo
http://oradical.uol.com.br/conteudo/balonismo_competicoes.asp
3. Jogo de dardos:
http://www.jogueaki.ig.com.br/jogos-online.php?jogo=501darts
http://www.explorelearning.com/index.cfm?method=cResource.dspDetail&ResourceID=138
4. Software Nippe Descartes
O grupo de pesquisa “Tecnologias no Ensino da Matemática”, vinculado ao Projeto Fundão, confeccionou diversas atividades utilizando o software Nippe Descartes, um aplicativo desenvolvido em Java que permite uma manipulação ágil e simples de janelas gráficas aplicáveis a qualquer página web. Este grupo reúne-se semanalmente e se propõe a desenvolver aplicações específicas para apresentação de conteúdos do Ensino Médio.
Página do Projeto Fundão: http://www.projetofundao.ufrj.br/matematica/
Para visualizar as atividades o professor deve:
1. Baixar o software Java disponível em: http://www.java.com/pt_BR/download/
2. Baixar o arquivo contendo as atividades.
Avaliação
Aplicação de problemas visando a avaliação do conteúdo apresentado.
O link abaixo apresenta sugestões de exercícios para serem aplicados ao final desta aula.
http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/ProbCondAluno.pdf
As soluções dos problemas propostos se encontram no link abaixo:
http://www.projetofundao.ufrj.br/matematica/atividades/portaldoprofessor/pdf/ProbCondProfessor.pdf
Sem estrelas 0 classificações
- Cinco estrelas 0/0 - 0%
- Quatro estrelas 0/0 - 0%
- Três estrelas 0/0 - 0%
- Duas estrelas 0/0 - 0%
- Uma estrela 0/0 - 0%
Denuncie opiniões ou materiais indevidos!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus