21/07/2009
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Fundamental Final | Matemática | Álgebra |
O que o aluno poderá aprender com esta aula
Introdução das operações algébricas
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Operações básicas
Estratégias e recursos da aula
Em sala de aula
Olá Professor, para iniciar o assunto “Operações Algébricas” com seus alunos, propomos uma atividade lúdica. O Jogo do Alvo.
Número de participantes: 3 a 5
Material: alvo, grãos de milho ou de feijão
Confecção do material:
Para que seus alunos confeccionem o alvo, peça a eles para construirem um conjunto de circunferências concêntricas com as seguintes especificações:
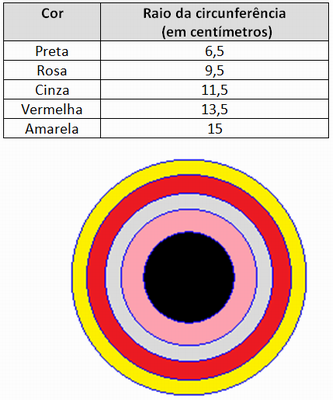
Para a faixa lateral, trace uma faixa na cartolina com as medidas indicadas no esquema. Corte o contorno, dobre a aba e picote como indicado. Cole as extremidades da faixa lateral e, em seguida, fixe-a ao redor do alvo.
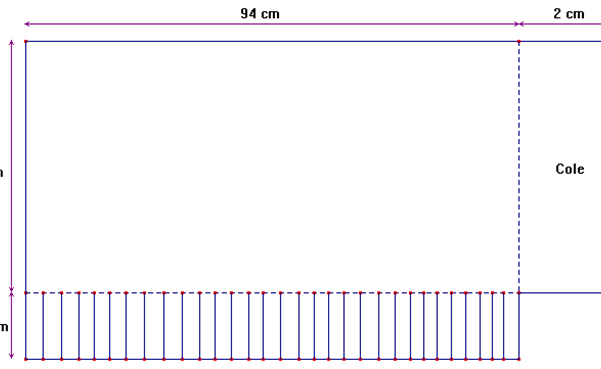
Regras:
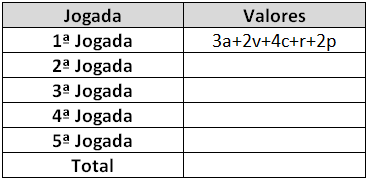
1. Cada aluno, na sua vez, joga 12 feijões no alvo. O jogador deve anotar cuidadosamente quantos feijões caíram em cada faixa, associando a quantidade de feijões com a cor da faixa. Em seguida, escreve uma adição para registrar esse fato e confere se o total de feijões anotado coincide com a quantidade de feijões jogada. Os jogadores devem jogar cinco rodadas, sempre fazendo as anotações.
2. Para simplificar a notação, é conveniente escolher uma única letra para representar cada cor e reescrever os resultados obtidos nas cinco rodadas, organizando-os como no exemplo abaixo. A utilização desse código facilita o registro.
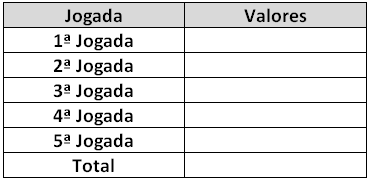
Observação: Pode haver divergência na escolha das letras, mas o resultado deve ser parecido.
3. Para facilitar os cálculos dos pontos, o jogador deve adicionar a quantidade de feijões que caiu em cada cor.
4. Ao final das cinco rodadas, cada jogador calcula o total de seus pontos, de acordo com os valores que o professor estipular para as cores.
Professor, comente com seus alunos que o objetivo da atividade é proporcionar um contato inicial com a Álgebra, por meio do trabalho com monômios e polinômios.
Professor oriente seus alunos da seguinte forma:
• Peça que o primeiro jogador que jogue os 12 feijões;
• Em cada rodada anote, na forma de monômio, o resultado apenas da quantidade de feijões que caiu na faixa vermelha. Por exemplo: se caíram 5 feijões na faixa vermelha, registre 5v.
• Escreva o monômio que representa o total dessas 5 rodadas.
Professor deixe que seus alunos brinquem um determinado tempo. Após este tempo faça alguns comentários. Supondo que o um determinado aluno obteve os s eguintes resultados:
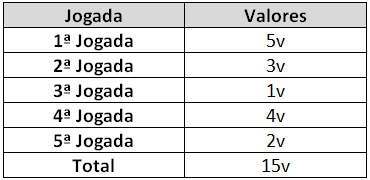
Comente com seus alunos que:
• A partir deste momento, eles começam a trabalhar com expressões que misturam números e letras, isto é, expressões literais ou algébricas.
• Os números e letras isolados ou ainda um agrupamento deles, relacionados por multiplicação, recebem o nome de monômios ou termo algébrico. Por exemplo: 5v, 3v e 1v.
• Cada monômio é constituído de uma parte numérica chamada coeficiente numérico e um conjunto de letras, chamada de parte literal ou incógnita.
• Monômios que têm a mesma parte literal são chamados de monômios semelhantes, e para adicionar monômios semelhantes eles deverão simplesmente calcular a soma dos coeficientes numéricos, mantendo a parte literal. Por exemplo: 5v + 3v + 1v + 4v + 2v = 15v, ou ainda, 10b2 – 8b2 =2b2.
• Quando o coeficiente numérico for igual a 1, ele não precisa ser escrito. Observe o exemplo: 1v, ou simplesmente, v.
• Quando se atribui números às letras de uma expressão literal e se efetua as operações indicadas na expressão numérica resultante, diz-se que o resultado obtido é um valor numérico dessa expressão literal. No nosso exemplo, se atribuíssemos para “v” o valor 19, o valor numérico da expressão literal seria 285, ou seja, como o total da tabela é 15v temos 15 x 19 = 285. Num primeiro momento, sugerimos que se atribua números inteiros e de pequeno valor (zero ou próximo de zero) às incógnitas e que, gradativamente, a dificuldade do cálculo numérico seja aumentada, podendo até utilizar números negativos.
Professor, vamos continuar a brincadeira com os alunos. Agora vamos utilizar todas as faixas de cores. Oriente seus alunos:
• O jogador deve anotar cuidadosamente quantos feijões caíram em cada faixa, associando a quantidade de feijões com a cor da faixa. Em seguida, escreve uma adição para registrar esse fato e confere se o total de feijões anotado coincide com a quantidade de feijões jogada, utilizando a forma de polinômios. Por exemplo, um aluno em uma determinada jogada, obteve 3 feijões na faixa cor amarela, 2 na faixa de cor vermelha, 4 na faixa de cor cinza, 1 na faixa de cor rosa e 2 na faixa de cor preta, deverá registrar os valores da seguinte forma:
Professor, novamente, deixe que seus alunos brinquem um determinado tempo. Após este tempo faça alguns comentários:
• Como já foi comentado, somente os monômios semelhantes podem ser adicionad os algebricamente. Quando os monômios não são semelhantes a adição permanece ape nas indicada. Nesse caso, tem-se, então, um polinômio.
• Em um polinômio é possível haver termos semelhantes. Quando isso ocorre, efetua-se a adição algébrica desses termos, mantendo os não semelhantes. O resultado é chamado de forma reduzida desse polinômio.
• A adição de polinômios pode ser organizada de várias maneiras. Vejamos alguns exemplos:
1ª maneira:
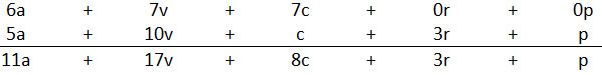
2ª maneira:
6a+7v+7c+0r+0p + 5a+10v+c+3r+p = 6a+5a+7v+10v+7c+c+0r+3r+0p+p=11a+17v+8c+3r+p
• Professor, novamente atribua valores para as incógnitas e peça a seus alunos para calcularem o valor numérico do polinômio. O vencedor da rodada será aquele que obtiver mais pontos.
No laboratório de informática
Professor leve seus alunos ao laboratório de informática. De preferência, acomode dois alunos em cada computador. Em seguida, peça a eles que acessem o sítio http://www.projetos.unijui.edu.br/matematica/principal/fundamental/raquel_leonogildo_gustavo_tania/projeto2MX.html, referente a uma aplicação para trabalhar com polinômios. Será apresentada a tela abaixo, nela, clique em entrar:
Em seguida serão apresentadas as atividades, no formato de catálogo. Selecione a primeira opção:
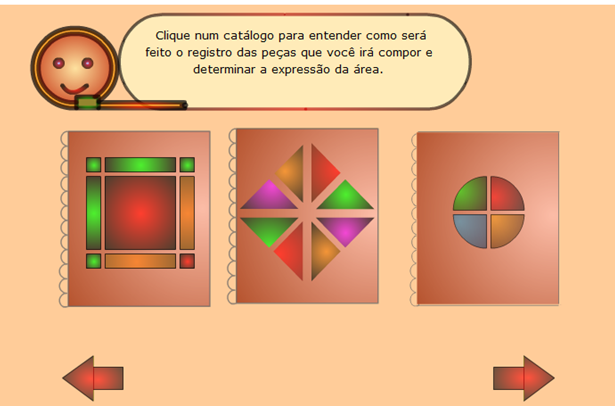
O aplicativo apresentará algumas telas com as instruções de utilização.
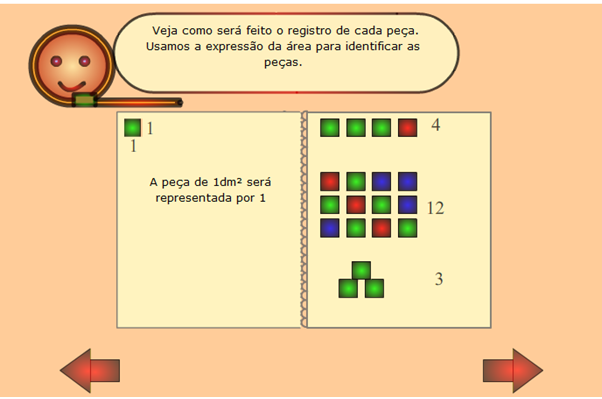
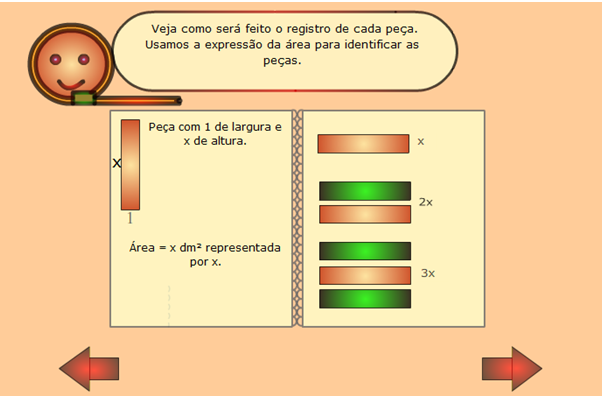
O procedimento, para formar um polinômio, será parecido com o da atividade em sala de aula. De acordo com as explicações do aplicativo, peça aos seus alunos que cliquem uma das figuras no canto superior direito, conforme a figura abaixo. Em seguida, arraste-a para o espaço do vitrô. Como cada peça tem o seu valor algébrico, é possível formar um polinômio. Peça aos seus alunos que registrem em uma folha de papel cada uma das peças selecionadas para formar o vitrô e o polinômio correspondente a expressão algébrica. Na parte debaixo da tela, existe um pequeno questionamento a ser respondido.

Professor, o aplicativo vai solicitar vários questionamentos iguais a este. Peça aos seus alunos que resolvam todos, registrando cada um dos questionamentos com as respectivas respostas.
Avaliação
A avaliação poderá ocorrer durante todas as atividades. Seja observando a exploração dos alunos e seus comentários, seja na resolução dos questionamentos propostos. No final das atividades poderá ser solicitado que os alunos façam atividades extraclasses contextualizadas referentes ao conteúdo proposto.
Quatro estrelas 3 classificações
- Cinco estrelas 1/3 - 33.33%
- Quatro estrelas 1/3 - 33.33%
- Três estrelas 1/3 - 33.33%
- Duas estrelas 0/3 - 0%
- Uma estrela 0/3 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Telma Bulhoes, Colégio da Policia Militar Luiz Tarquinio , Bahia - disse:
bulhoes.telma@gmail.com14/06/2012
Cinco estrelasAchei a aula maravilhosa e bastante prática. Desta forma facilita bastante a aprendizagem do aluno na questão algébrica.
-
delmafialho, E.E. MIGUEL GONTIJO , Minas Gerais - disse:
delmafialho@yahoo.com.br14/04/2010
Quatro estrelasmuito boa a aula.
-
Maria Luiza Barone, licencianda da UNIP ead , São Paulo - disse:
luzbarne@yahoo.com.br24/03/2010
Três estrelasAchei bem interessante. Atrai a atenção dos alunos, internaliza o sentido das literais e dos coeficientes, da possibilidade de somar-se apenas os semelhantes; visualmente as cores são atraentes.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


