Esta é uma segunda aula idealizada a partir de experimentos envolvendo o lançamento aleatório de discos em quadriculados ou ladrilhados planos, pertinente ao primeiro módulo do Matem@tica na Pr@tica, um curso de especialização em matemática inserido no Plano de Ações Articuladas do MEC. Nessas aulas o ensino/aprendizagem de probabilidade é viabilizado de forma significativa através da construção do conhecimento a partir da experimentação, possibilitando um maior envolvimento do estudante com o tema probabilidade e permitindo uma maior cooperação e reflexão entre eles.  

Esta segunda aula foi idealizada a partir do jogo dos discos. Os estudantes irão aprender a estimar a probabilidade de um disco de determinado diâmetro, lançado aleatoriamente em um quadriculado, parar dentro de um quadrado sem tocar nem sobrepor as linhas do quadriculado. Lançando discos de diversos diâmetros, poderão obter uma tabela diâmetro versus probabilidade e construir, por ajuste de curva, uma aproximação do gráfico da probabilidade em função do diâmetro dos discos e estudar algumas propriedades desse fenômeno.

O estudante deve conhecer o cálculo elementar de probabilidades, na forma de uma divisão entre a quantidade de eventos favoráveis e a quantidade total de eventos. É importante ainda que os estudantes saibam utilizar tabelas para organizar dados e saibam representar esses dados em um gráfico em um sistema de coordenadas cartesianas.

Esta aula está dividida em quatro momentos. No primeiro momento sugerimos a apresentação de uma situação-problema interessante para os estudantes. No segundo momento, os estudantes deverão realizar experimentos com lançamentos de discos em um piso quadriculado e obter tabelas de dados. No terceiro momento, eles deverão trabalhar com estes dados, construindo um gráfico por ajuste de curvas. No quarto momento, sugerimos o fechamento da atividade com uma análise coletiva dos resultados e a resolução do problema proposto no primeiro momento.

Primeiro momento: apresentação do problema

Uma forma de iniciar a aula é apresentar para os estudantes uma situação-problema. O problema pode ser apresentado antecipadamente, para que os estudantes possam estudá-lo e imaginar métodos para resolvê-lo. Nesse caso, o professor deve contar com a possibilidade de eles procurarem informações na internet. A seguir sugerimos um formato básico do problema, mas o professor pode construir outras versões.   

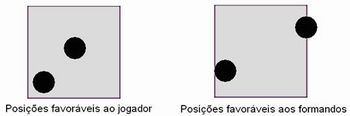
Na festa anual promovida por sua escola, os estudantes do terceiro ano do ensino médio resolveram montar uma barraca para arrecadar fundos para a realização da tão sonhada festa de formatura. Alguns estudantes queriam montar uma barraca de doces, outros queriam vender refrigerantes e salgados, mas a maior parte da turma pensou em bolar um jogo de apostas. Só faltava saber qual seria o jogo, que deveria ser simples e interessante. Depois de muita discussão e nenhuma definição, a turma resolveu pedir ajuda ao professor de Matemática. O professor levou a turma para o pátio da escola e mostrou o piso quadriculado com ladrilhos quadrados de 30 cm de lado. O professor fez a seguinte sugestão:

"Que tal fazer um jogo de apostas de lançamento de discos? A ideia é construir discos com um certo diâmetro, e os convidados compram o direito de jogá-los aleatoriamente no piso. Se o disco, depois de parar, ficar inteiramente dentro de um ladrilho, sem tocar ou interceptar as linhas de separação do ladrilhamento, o convidado ganha a aposta e recebe um prêmio. Se o disco tocar alguma das linhas, vocês ganham a aposta e ficam com o dinheiro da compra dos discos

Os estudantes adoraram a ideia e, na mesma hora, começaram a pensar qual seria o melhor diâmetro para os discos. Claro que, quanto maior, melhor, pensaram...   O professor completou:   Vocês só precisam tomar cuidado na hora de determinar o diâmetro desses discos, pois os convidados da festa somente irão se interessar pelo jogo se acharem que têm chances de ganhar o prêmio. Agora me digam: qual seria o diâmetro ideal? Vamos resolver esse problema em sala de aula?"

Depois de apresentar o problema para a turma, o professor deve dar algum tempo para que pensem e coloquem alguns possíveis métodos para resolver esta questão. Seria interessante discutir estes métodos com a turma em sala de aula. Após este momento inicial de discussão, o professor deve propor aos estudantes que realizem o jogo. A partir daí a turma deve ser organizada para a realização do experimento.

Segundo momento: experimentando o lançamento de discos

Existem duas formas de abordar esse problema: a experimental e a teórica. A abordagem teórica está disponível em artigos na internet, e você pode encontrar alguns deles nos recursos complementares desta aula. Os estudantes também podem acessar estes artigos e resolver o problema usando a definição de probabilidade geométrica. Nesta aula sugerimos ao professor propor aos estudantes que resolvam o problema através da abordagem experimental.

A seguir descrevemos o local e os materiais necessários para desenvolver os experimentos.

1. Procurar na escola um local com piso ladrilhado, bem nivelado e liso, com ladrilhos quadrados de mesmo lado. Um piso que funciona bem é um que tem quadrados de 30 cm de lado. O local deve ter espaço suficiente para que vários grupos de estudantes possam fazer os lançamentos.   
2. Arrumar discos de vários diâmetros. Esses discos podem ser de borracha ou de papelão. Uma possibilidade é adquirir anéis de vedação de canos que são vendidos em lojas de material de construção. É bom ter discos de cinco ou seis diâmetros diferentes, com valores que variem entre zero e o valor do lado dos quadrados. O experimento leva menos tempo se tivermos 10 discos de cada diâmetro.   
3. Na hora do experimento, disponibilizar folhas de atividade (conforme sugestão abaixo) ou, na falta do roteiro, folhas para anotações, lápis, borracha, régua e folhas milimetradas para fazer gráficos. Nesse caso, podem ser preparadas com antecedência folhas com tabelas para anotar os lançamentos.

Caso sua escola não possua um piso ladrilhado, o professor poderá desenhar o quadriculado no piso da escola. Outra alternativa é simular o jogo em um quadriculado em papel cartolina e fazer o lançamento com moedas e botões de diferentes diâmetros.   

Depois que o professor tiver disponibilizado os materiais, o experimento pode ser realizado. Divida os estudantes em grupos, distribua o roteiro e os conduza para o local da escola onde serão realizados os experimentos. É importante que todos se envolvam com o experimento para depois responder as questões que se encontram no roteiro.   

Na hora de fazer os experimentos, o professor pode ler o roteiro com os estudantes, explicando o que deverá ser feito, ou dar um tempo para que eles leiam sozinhos. Em seguida, deve dar a cada grupo discos com o mesmo diâmetro (dez discos de preferência). Depois disso, poderão começar a realizar os lançamentos e anotar os lançamentos favoráveis. O ideal é que cada grupo faça pelo menos 200 lançamentos, que podem ser feitos de dez em dez. A cada dez lançamentos, os estudantes contam aqueles favoráveis (em que o disco caiu inteiramente dentro de um ladrilho) e anotam no roteiro. Solicite que os lançamentos sejam realizados sem mira, de olhos fechados ou de costas para o ladrilhado, para garantir que não haja nenhuma tendência no local onde o disco irá parar no piso.

Terceiro momento: calculando a probabilidade de lançamentos favoráveis

Após realizarem os lançamentos e anotarem aqueles favoráveis, os estudantes irão trabalhar com os dados.   

A primeira análise será o cálculo da estimativa experimental da probabilidade para aquele diâmetro d (do disco lançado pelo grupo). Para que os estudantes calculem esta probabilidade, lembre-os que a probabilidade é o quociente dos lançamentos favoráveis (LF) pelo total de lançamentos (TF).

p(d) = LF / TF

Depois da análise dos seus dados, cada grupo deverá anotar os resultados dos demais grupos da turma, construindo uma tabela com os diâmetros dos discos e as probabilidades de lançamentos favoráveis para cada diâmetro. Com os dados de toda a turma, pode ser construído um gráfico da probabilidade de um lançamento favorável em função do diâmetro do disco.

Comentário: 

Para ajudar o professor a pensar sobre esta atividade que estamos propondo, apresentamos abaixo um exemplo real de um experimento deste tipo que foi feito em uma escola. Os estudantes eram do segundo ano do Ensino Médio da Escola Estadual Washington Luiz, localizada em Porto Ferreira, SP. O experimento foi orientado pela Profa. Gracia Aparecida de Almeida Sicheroli, em 2001. Os lançamentos foram feitos em um piso quadriculado com quadrados de 30 cm de lado. Começamos com os resultados de um grupo.

Diâmetro dos discos = 6 cm

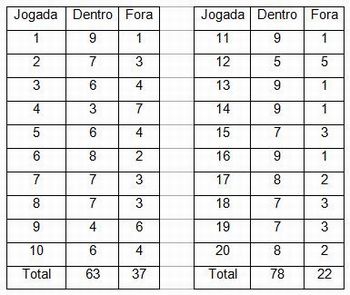
Esse grupo fez 20 jogadas com dez discos de 6 cm em cada vez, totalizando 200 lançamentos. Vemos que obteve uma aproximação da probabilidade para o disco de 6 cm de

p(6) = 141 / 200 = 0,705 = 70,5%

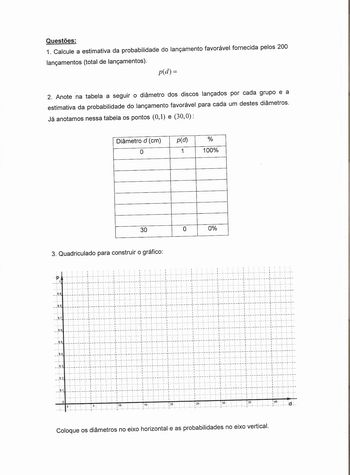
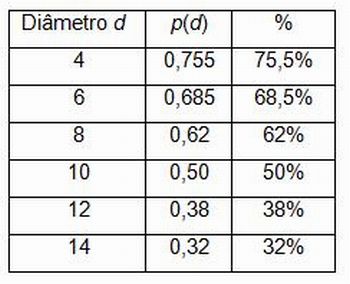
Reunindo os dados de todos os grupos, a classe construiu a seguinte tabela:

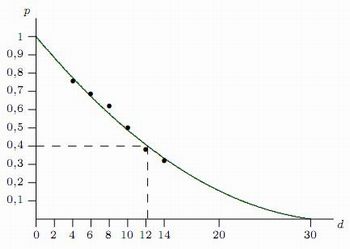
Essa tabela foi utilizada para fazer um gráfico em um sistema de coordenadas cartesianas, primeiro com os pontos (d,p(d)) , acrescentando-se os pontos (0,1)  e (30,0) , e depois desenhando a curva contínua do gráfico, ajustando-a aos pontos. O ponto (0,1) corresponde a um disco imaginário de diâmetro zero, com probabilidade teórica p(0)=1. Já o ponto (30,0) corresponde a um disco com diâmetro d=30, igual ao lado do ladrilho. Nesse caso, o disco sempre toca as linhas do ladrilhado, determinando uma probabilidade p(30)=0.

Obtiveram então o seguinte gráfico:

Quarto momento: voltando ao problema inicial

Depois que os estudantes tiverem preenchido as tabelas e montado o gráfico, o professor pode propor uma discussão coletiva com a turma, comparando os gráficos. Em seguida, o professor deverá voltar ao problema dos formandos, que é o de determinar o diâmetro dos discos a serem construídos para o jogo de apostas, visando arrecadar fundos para a formatura. Suponhamos que os formandos decidam que o jogo deve ser 40% favorável ao jogador. Assim, o jogo é favorável aos formandos, mas não muito. Os estudantes poderão encontrar o diâmetro correspondente a 40% (=0,4) usando o gráfico. Na atividade desenvolvida na Escola Estadual Washington Luiz, em Porto Ferreira, SP, dá para ver na tabela que esse diâmetro deve ser aproximadamente de 12 cm.

Isso também pode ser confirmado pelo gráfico, conforme mostrado acima, traçando primeiro uma linha horizontal pela ordenada 0,4 e depois a linha vertical pelo ponto de interseção com o gráfico. Essa linha passa perto do ponto (12,0), indicando o diâmetro de 12 cm. O professor pode apontar o fato de que o gráfico é melhor do que a tabela. Por exemplo, se os formandos resolverem que o jogador só deve ter 20% de chance, então o gráfico ajuda mais do que a tabela para encontrar o diâmetro.

Calculamos que os estudantes necessitam, em condições normais, de uma aula de 45 minutos para construir a tabela e de outra aula, também de 45 minutos, para fazer o gráfico e analisar soluções para o jogo.

Uma aula adicional de 45 minutos pode ser usada para o estudo da solução exata do jogo. A probabilidade exata do lançamento favorável para um determinado disco pode ser obtida aplicando-se a definição de probabilidade geométrica.

Para mais detalhes confira:   

[1] Paterlini, R. R. O Problema do Jogo dos Discos. Revista do Professor de Matemática no. 48, 1o quadrimestre de 2002, p. 13-20. Republicado em Matemática Ensino Médio, Coleção Explorando o Ensino, vol. 3, Brasília, Ministério da Educação, 2004.   

[2] Paterlini, R. R. Aula sobre o Problema do Jogo dos Discos. Hipertexto Pitágoras. Departamento de Matemática, UFSCar, 2002.  http://www.dm.ufscar.br/hp/hp205/hp2053/hp2053001/hp2053001.html
 

A aprendizagem dos estudantes poderá ser avaliada através da análise da tabela, do gráfico e da conclusão sobre o problema dos formandos. Os seguintes itens podem ser levados em conta pelo professor:   

1. O cuidado que o grupo teve nos lançamentos dos discos e na contagem dos eventos favoráveis.
2. A construção cuidadosa da tabela e o acerto dos cálculos sobre as estimativas das probabilidades.
3. O capricho na construção do gráfico.
4. Se o grupo soube terminar o problema dos formandos, propondo uma probabilidade adequada de acerto para o jogador e em seguida determinando corretamente o diâmetro dos discos a serem utilizados no jogo.