27/09/2012
Suelen Fernanda Machado
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Álgebra |
| Ensino Médio | Matemática | Números e operações |
O que o aluno poderá aprender com esta aula
Compreender e conceituar a lógica na matemática.
Compreender noções de proposição e paradoxo.
Entender e empregar elementos da lógica na resolução de problemas.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
- Leitura, interpretação e produção de texto e resolução de problemas.
Estratégias e recursos da aula
Organização da Aula
Para essa aula, o professor pode solicitar aos alunos que antecipadamente, se possível, leiam o livro "Alice no País das Maravilhas" e "Através do espelho e o que Alice encontrou lá" de Lewis Carrol. Outra possibilidade é que vejam o filme de Tim Burton "Alice no Pais das Maravilhas". Também é possível ver o teaser do filme “Alice in Wonderland Teaser 1”, com a duração de 1:41min. Tal filme corresponde a uma chamada para atrair o telespectador para o filme “Alice in Wonderland (Alice no País das Maravilhas) de Tim Burton, lançado no ano de 2010. Ver: http://www.youtube.com/watch?v=LjMkNrX60mA.
Como referência, o professor poderá obter mais informações sobre o livro e o filme nos seguintes sites:
- Alice no País das Maravilhas
http://pt.wikipedia.org/wiki/Alice_no_Pa%C3%ADs_das_Maravilhas.
- Filme Alice in Wonderland
http://www.imdb.com/title/tt1014759.
- Lewis Carroll
Sobre o autor

Atividade 1
Problema 1
Problema 2
Problema 3

| Seg. | Ter. | Qua. | Qui. | Sex. | Sab. | Dom. | |
| Leão | M | M | M | V | V | V | V |
| Unicórnio | V | V | V | M | M | M | V |
Atividade 2


A partir de uma proposição e dos conectores, podemos construir uma outra proposição correspondente com a sua negação; e com duas ou mais.
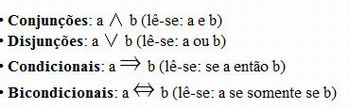
Assim, seja a sentença:
“Se Maria é estudiosa então ela passará no Vestibular”.
Sejam as proposições:
p = “Maria é estudiosa”.
q = “Ela passará no Vestibular”.
Daí, poderemos representar a sentença da seguinte forma: Se p então q ( ou p ⇒q ).
Atividade 3
Considerem as proposições e traduzam para a linguagem natural:
p: "Está quente".
q: "Está frio".

Respostas:
a) Não está quente
b) Não está frio.
c) Está quente ou está frio.
d) Está quente e está frio.
e) Se está quente então está frio.
f) Se está quente então não está frio.
g) Está quente se somente se está frio.
Atividade 4

Recursos Educacionais
| Nome | Tipo |
|---|---|
| A lógica de Alice | Vídeo |
| Alice, os paradoxos e a formalização | Vídeo |
| A revanche de Alice | Vídeo |
Recursos Complementares
Brincando com a Lógica: Aprendendo a Pensar. Disponível em: http://www.feg.unesp.br/extensao/teia/trab_finais/TrabalhoMichele.pdf, acesso em 04 de setembro de 2012.
Aristóteles lógica. Disponível em: http://objetoseducacionais2.mec.gov.br/handle/mec/14703, acesso em 04 de setembro de 2012.
Avaliação
A avaliação deverá ser realizada ao longo das aulas, observando os alunos nos seguintes critérios:
1. Desenvolvimento e socialização no grupo na resolução dos problemas. Se concentrou no desenvolvimento das atividades? Contribuiu na discussão?
2. No desenvolvimento do raciocínio lógico? O aluno foi argumentativo? A produção no grupo foi pertinente?
3. Durante a apresentação dos vídeos, o grupo do aluno formulou conceitos? Auxiliou ou solicitou auxílio dos colegas.
4. Participação individual e coletiva dos alunos no desenvolvimento do contexto geral da aula.
Um meio que pode contribuir para a verificação de aprendizagem dos alunos é sempre solicitar aos alunos que realizem anotações no caderno referente ao contexto da aula para registro de suas aprendizagens. Que diariamente relatem o que aprenderam e como aprenderam. Esses relatos podem contribuir para que o professor perceba os caminhos que os alunos vem fazendo, bem como avaliar suas aprendizagens.
Duas estrelas 3 classificações
- Cinco estrelas 0/3 - 0%
- Quatro estrelas 1/3 - 33.33%
- Três estrelas 1/3 - 33.33%
- Duas estrelas 0/3 - 0%
- Uma estrela 1/3 - 33.33%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Helen Otoni, ESEBA , Minas Gerais - disse:
helen_otoni@yahoo.com.br04/09/2013
Quatro estrelasExcelente abordagem. Usarei com meus alunos.
-
Robson, Universidade Catolica de Brasilia , Minas Gerais - disse:
robson.avilaucb@gmail.com09/08/2013
Uma estrelagostaria de dizer que o video esta sem audio.
-
Abimael A. Ribeiro, SEEDUC/ma , Maranhão - disse:
ribeiro.abimael@bol.com.br20/10/2012
Três estrelasEntendo que esse tipo de aula deve ser propostas para os alunos do primeiro ano do ensino médio .Infelizmente os livros textos atuais não trazem mais esse assunto que é de muita importância para o desenvolvimento do racíocinio lógico dos alunos.Serve também para ampliar os conhecimentos e interagir com outras disciplinas estabelecendo a interdisciplinaridade.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


