20/09/2013
Ângela Cristina dos Santos e Antomar Araújo Ferreira
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Fundamental Inicial | Matemática | Números e operações |
O que o aluno poderá aprender com esta aula
A fim de desenvolver as competências da área 1 da matriz do ENEM, que é o de construir significados para os números naturais, inteiros, racionais e reais e as operações matemáticas envolvendo estes números, esta aula tem por objetivo ajudar o aluno na compreensão do que é dividir um número natural por outro, utilizando a ideia de quantas vezes um valor “cabe” dentro de outro.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Subtração
Multiplicação
Estratégias e recursos da aula
RECURSOS MATERIAIS
Caderno para registros.
Folhas de papel quadriculado.
Lápis colorido.
ESTRATÉGIAS:
A aula
1º MOMENTO:
Comentário: Quando o algoritmo da divisão é trabalhado em sala de aula, muitas vezes os alunos apresentam dificuldades em efetuar divisões simples como:5 ÷ 1; 12 ÷ 3; 15 ÷ 4, etc.
Esta aula tem por objetivo levar o aluno a visualizar estas divisões utilizando a ideia de quantas vezes uma quantidade cabe dentro de outra. Está ideia está intimamente ligada ao fato de divisão e multiplicação serem operações inversas.
Utilize como recurso o papel quadriculado que é de baixo custo e pode ser utilizado para trabalhar diversos conteúdos dentro da matemática. Sugerimos que um caderno de folha quadriculada seja incluído na lista de materiais solicitados pela escola aos alunos no início do ano.
Inicie a aula dizendo aos alunos que aprenderão a dividir valores de uma forma diferente. No caderno de matemática eles devem escrever o título “Quanto Cabe?”. Em seguida, solicite que os alunos deem sugestões de divisões de números com até 2 algarismos por números de 1 ou 2 algarismos (conforme a maturidade da turma). Incentive-os a pensarem em situações pelas quais eles já passaram e que tiveram que realizar uma divisão (dividir dinheiro, objetos, cartas em jogos ou pessoas para formar grupos ou times). Se achar conveniente, registre estas situações em forma de problemas no quadro ou registre apenas as divisões. Todos os alunos devem copiar no caderno.
Utilize as seguintes divisões como exemplos para o desenvolvimento desta aula:
5 ÷ 1; 12 ÷ 3; 15 ÷ 4; 36 ÷ 3; 50 ÷ 10 e70 ÷ 12.
Entregue aos alunos uma folha de papel quadriculado e para resolver a primeira divisão, 5 ÷ 1, solicite que eles recortem na folha um retângulo que tenha 5 quadradinhos e colem no caderno. Após colarem eles devem colorir grupos que tenham 1 quadradinho. Cada grupo deve ser colorido de uma cor (figura 1). Logo em seguida, questione:
“Quantos grupos de 1 quadradinho foi possível colorir com 5 quadradinhos?”
“Podemos dizer que a quantidade 1 cabe quantas vezes dentro da quantidade 5?”
Resposta esperada: Espera-se que os alunos respondam 5.
Solicite que os alunos registrem no caderno: a quantidade 1 cabe 5 vezes dentro da quantidade 5, portanto, podemos dizer que 5 dividido por 1 é igual a 5, porque 5 x 1 = 5.
Figura 1: Representação da divisão 5 ÷ 1
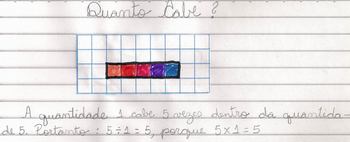
Fonte: Arquivo da Autora
Agora, para resolver a divisão 12 ÷ 3, solicite que façam um retângulo com 12 quadradinhos. Para isso, sugira que pensem em uma multiplicação cujo resultado é 12 (12 x 1; 6 x 2 ou 3 x 4). Um fator da multiplicação será a quantidade de quadradinhos da largura e o outro da altura do retângulo. Colem o retângulo no caderno e coloram grupos de 3 quadradinhos, cada grupo de uma cor (figura 2).
Questione:
“Quantos grupos foram formados?”
“Quantas vezes a quantidade 3 cabe dentro da quantidade 12?”
“Sobrou algum quadradinho sem colorir?”
Respostas esperadas: 4 e não sobrou quadradinho.
Solicite que os alunos registrem no caderno: a quantidade 3 cabe 4 vezes dentro da quantidade 12, portanto, podemos dizer que 12 dividido por 3 é igual a 4 e não resta nada, porque 4 x 3 = 12.
Figura 2: Representação da divisão 12 ÷3
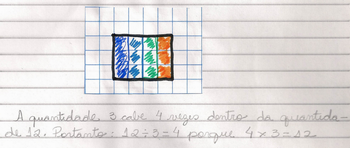
Fonte: Arquivo da Autora
Agora, para resolver a divisão 15 ÷ 4, solicite que façam um retângulo com 15 quadradinhos. Sugira que pensem em uma multiplicação cujo resultado é 15 (15 x 1; 3 x 5). Colem o retângulo no caderno e coloram grupos de 4 quadradinhos, cada grupo de uma cor (figura 3).
Questione:
“Quantos grupos foram formados?”
“Quantas vezes a quantidade 4 cabe dentro da quantidade 15?”
“Sobrou algum quadradinho sem colorir?”
Respostas esperadas: 3 e sobraram 3 quadradinhos.
Solicite que os alunos registrem no caderno: a quantidade 4 cabe 3 vezes dentro da quantidade 15. Portanto, podemos dizer que 15 dividido por 4 é igual a 3 e restam 3 quadradinhos, porque quando pensamos na tabuada do 4, o resultado que mais se aproxima de 15, sem passar, é 12. Podemos registrar: 15 ÷ 4 = 3, pois15 = 3 x 4 + 3.
Figura 3: Representação da divisão 15 ÷ 4
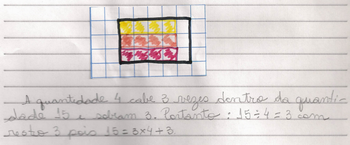
Fonte: Arquivo da Autora
Repita o procedimento com as outras divisões sempre registrando as conclusões (Figura 4).
Figura 4: Outras divisões
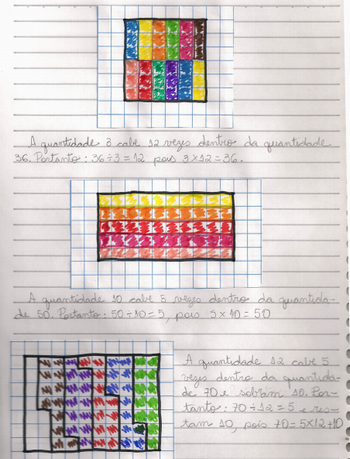
Fonte: Arquivo da Autora
Recursos Complementares
Jogo para crianças que estão aprendendo o conceito de divisão:
http://www.somatematica.com.br/matkids/dividir.html
acesso em setembro de 2013.
Avaliação
Professor considere a participação dos alunos durante as atividades, a execução dos exercícios e a organização do caderno como instrumentos de avaliação.
Além disso, para verificar se os alunos entenderam que o resultado da divisão é o número de vezes que o divisor cabe dentro do dividendo, acrescentado do resto quando houver, solicite que os alunos preencham as lacunas das sentenças abaixo:
a) Se temos 30 crianças para formarmos times de 6 jogadores, teremos _______ times, pois 6 cabe ______ vezes em 30.
b) Se temos uma caixa com 25 bombons para dividir entre 3 crianças, cada criança receberá ______ bombons e restará ______ bombom na caixa, pois a quantidade 3 cabe______vezes dentro de 25 e sobra __________.
c) 25 ÷ 5 =______, pois 5 x ______= 25.
d) 18 ÷ 8 = ______, e restam ________pois 8 x ______= ______ e _____+ ______ = 18
RESPOSTAS ESPERADAS:
a) Se temos 30 crianças para formarmos times de 6 jogadores, teremos 5 times, pois quando pegamos a quantidade 6, 5 vezes obtemos 30.
b) Se temos uma caixa com 25 bombons para dividir entre 3 crianças, cada criança receberá 8 bombons e restará 1 bombom na caixa, pois a quantidade 3 cabe 8 vezes dentro de 25 e sobra 1 .
c) 25 ÷ 5 = 5, pois 5 x 5 = 25.
d) 18 ÷ 8 = 2, e restam 2 pois 8 x 2= 16 e 16 + 2 = 18.
Quatro estrelas 2 classificações
- Cinco estrelas 1/2 - 50%
- Quatro estrelas 0/2 - 0%
- Três estrelas 1/2 - 50%
- Duas estrelas 0/2 - 0%
- Uma estrela 0/2 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Prof. Isidio Valadares, Isidio Valadares , Mato Grosso - disse:
valadares.valadares@outlook.com02/09/2015
Três estrelasmuito boa a aula. Parabéns aos autores!!
-
Sabrina Zilli, Colégio Dom Rafael , Santa Catarina - disse:
sabrina.zilli@gmail.com02/10/2013
Cinco estrelasGostei muito da ideia. Irei utilizar o modelo da aula com os meus estudantes do terceiro ano! Obrigada!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


