16/06/2014
Angela Cristina dos Santos; Antomar Araújo Ferreira
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Fundamental Final | Matemática | Espaço e forma |
| Ensino Fundamental Final | Matemática | Grandezas e medidas |
O que o aluno poderá aprender com esta aula
Esta aula busca desenvolver as competências das áreas 2 e 3 da Matriz de Referência de Matemática e sua Tecnologias do ENEM, que são, respectivamente:
- utilizar o conhecimento geométrico para realizar a leitura e representação da realidade e agir sobre ela;
- construir noções de grandezas e medidas para a compreensão da realidade e a solução de problemas do cotidiano.
Mais especificamente, busca avaliar as habilidades:
- utilizar conhecimentos geométricos de espaço e forma na seleção de argumentos propostos como solução de problemas do cotidiano (H9);
- avaliar proposta de intervenção na realidade utilizando conhecimentos geométricos relacionados a grandezas e medidas (H14).
Para isto são propostos para essa aula o seguinte objetivo:
- Conceituar a área e o perímetro de um retângulo;
- Verificar que o valor do perímetro de um retângulo pode ser alterado, em função das dimensões da mesa utilizada.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
- Área do retângulo;
- Perímetro do retângulo.
Estratégias e recursos da aula
Além dos recursos geralmente presentes em sala de aula, como a lousa, a figura 1 poderá ser utilizada, bem como folhas A4.
A aula
1º MOMENTO:
Professor(a), inicie a aula problematizando:
O que devemos considerar para distribuir uma quantidade de pessoas ao redor uma mesa retangular: o perímetro ou a área da mesa?
Padrão de resposta esperada: O perímetro, pois quanto maior o comprimento ou a largura, mais gente pode se sentar ao seu redor.
COMENTÁRIOS:
1 – Alguns alunos podem apresentar dúvidas, nesse caso, apresente uma situação cotidiana ou se na sala de aula houver carteiras: separe uma mesa e questione quantas cadeiras ou pessoas (sem cadeiras) podem ser dispostas ao redor dela. Em seguida, coloque duas mesas juntas e questione se uma das dimensões aumentou (comprimento ou largura – uma delas vai se manter), se o perímetro aumentou – essa questão é perceptível visualmente – e quantas cadeiras ou pessoas podem ser dispostas nessa nova situação.
2 – Se necessário retome o conceito de perímetro como sendo a medida do contorno de uma figura geométrica plana.
Com um perímetro maior mais pessoas podem se sentar a mesa, no entanto, isso não garante que seja possível colocar mais itens sobre a mesma. Sendo assim, questione:
O que devemos considerar para distribuir uma quantidade de objetos sobre uma mesa retangular: o perímetro ou a área da mesa?
É provável que muitos(as) alunos(as) estabeleçam uma relação parecida com a que concluíram com o perímetro, isto é aumentando as dimensões de uma mesa, aumenta-se também o espaço para se colocar objetos. Para desfazer essa ideia solicite aos alunos que observem a figura 1 a seguir e que considerem as medidas em centímetros:
Figura 1: Esboço de mesa com aproximadamente 8 cm de largura

Fonte: arquivo do autor
Questione:
Nessa mesa cabem muitos objetos?
Espera-se que os alunos observem que o perímetro da mesa é de aproximadamente 935 cm, no entanto, é uma mesa na qual não se poderia apoiar tantos objetos, uma vez que sua largura é menor que 8 cm.
Professor(a), oriente as discussões com outro questionamento:
Agora que já perceberam que para obtermos uma mesa utilizável não podemos usar quaisquer medidas, vamos determinar qual o perímetro e área da mesa da figura 2?
Figura 2: Superfície da mesa

Fonte: Arquivo do autor
Perímetro: 4 . 60 = 240 cm
Área: 60 . 60 = 360 cm⊃2;
Continue instigando...
Nessa mesa, a área é menor que a área da mesa anterior, ela cabe mais objetos?
Esse é um momento de revisão, no qual os estudantes terão a oportunidade de relembrar, caso necessário, os meios para determinar perímetro e área de retângulos.
Feitas essas considerações, retome o tema central dessa aula: estabelecer uma relação entre área e perímetro do retângulo.
2º MOMENTO:
Parte 1: Relacionando a área e o perímetro de uma superfície retangular com suas dimensões.
Professor(a), inicie esse momento, apresentando a mesa dobrável por meio da figura 3 ou qualquer outra fonte que achar pertinente.
Figura 3: Mesa dobrável entreaberta

Fonte: Arquivo do autor
Professor(a), explique aos estudantes que se trata de um tipo de mesa que oferece regulagens para a área de sua superfície.
Em seguida, apresente o vídeo disponível no endereço: http://www.youtube.com/watch?v=Ob-wxAE0Y1c (Acesso em 03 mai 2014).
A partir daí, problematize:
No vídeo, quando a mesa é aberta o que acontece com as suas dimensões? E em relação ao perímetro e a área?
COMENTÁRIO: Espera-se que os(as) alunos(as) manifestem respostas como: as dimensões (comprimento e largura) dobram, por isso obtém-se o dobro de área e o dobro do perímetro.
Nesse momento, trabalhe com a folha de papel, dando preferência a rascunhos para evitar desperdícios, e solicite aos estudantes que dobrem a folha ao meio, simulando a mesa elástica, e que observem o que acontece, confrontando com o que acabaram de dizer.
Nesse momento, reserve um espaço para os alunos discutirem e socializarem suas considerações. Espera-se que, com as discussões, os alunos observem que, no caso o valor da área dobra, mas que o perímetro não.
COMENTÁRIO: Caso se dobre a área, um dos lados de cada retângulo é desconsiderado para calcular o perímetro.
Figura 4: Superfície da mesa aberta

Fonte: Arquivo do autor
Em seguida, peça aos alunos que calculem a área e o perímetro da mesa aberta, assim:
Área:
(60 + 60) . 60 = 120 . 60 = 7200 cm⊃2;.
Ao ilustrar que a área dobra, pode-se, ainda, desenvolver os cálculos da seguinte maneira:
(60 + 60) . 60 =60 . 60 + 60 . 60 = 360 + 360 = 7200 cm⊃2;
No entanto, como podemos observar na figura 4, há um lado em comum entre os polígonos quando a mesa está aberta. Observe a figura 5:
Figura 5: Esboço da mesa aberta
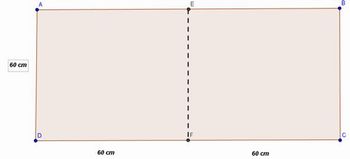
Fonte: Arquivo do autor
O perímetro com a mesa fechada era de 240 cm, contudo, com a nova configuração o perímetro é de 2 . 60 + 2 . (60 + 60) = 120 + 240 = 360 cm. É possível ainda fazer a abordagem de maneira a utilizar o dobro do perímetro e subtrair o que não é necessário, portanto, 2 . 240 – (60 + 60) = 480 – 120 = 360 cm.
COMENTÁRIO: Questione também sobre a forma de encontrar o perímetro desconsiderando os lados em comum, ou seja, desconsiderando EF.
Professor(a), a situação apresentada pode ser analisada de forma genérica, para isso deve-se usar os conhecimentos algébricos.
Vamos generalizar?!
Para estabelecer a relação genérica (algébrica) entre a área e o perímetro de uma superfície retangular com suas dimensões, deve-se atribuir a cada dimensão uma variável.
COMENTÁRIO: Professor(a), se achar conveniente, revise com os alunos a diferença entre incógnita e variável.
Agora, tente algebrizar a situação, assim:
Em síntese, nesse caso em particular “saímos” de uma mesa com “x” de área e “y” de perímetro para uma com “a” de área e “b” de perímetro.
Professor(a), mostre outra possibilidade, caso a mesa abrisse para um lado perpendicular ao mostrado na figura, ou seja, ao observar a figura, ao invés de abrir para a direita, abrisse para cima. Trabalhe o caso mais simples, em que a mesa fechada é um quadrado. Esse encaminhamento pode ser compartilhado com os estudantes, ficando a critério do(a) professor(a), uma vez que o raciocínio para os cálculos é semelhante.
A partir daí professor(a), faça a seguinte pergunta:
Como poderíamos escrever essa relação para um caso geral, em que a mesa “fechada” tivesse dimensões x e y (figura 6)?
Figura 6: Mesa fechada com dimensões x e y
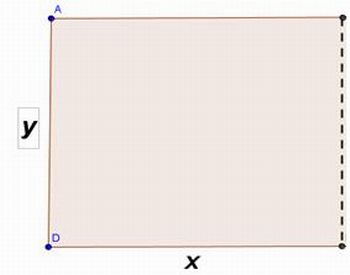
Fonte: Arquivo do autor
Espera-se que, a partir das discussões anteriores, os alunos respondam que:
- Área: x . y
- Perímetro: 2x + 2y
Nesse momento, continue os questionamentos:
Sem mudar o valor das dimensões (x e y) da mesa, como podemos escrever a área e o perímetro, para um caso geral, em que a mesa “aberta?
Figura 7: Mesa aberta
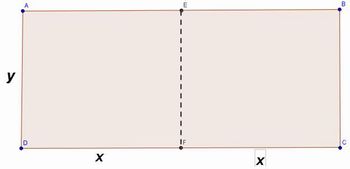
Fonte: Arquivo do autor
Desse modo, espera-se que os alunos cheguem a às respostas.
- Área: 2.x.y
- Perímetro: 2 . (2x + 2y) – (y + y) = 4x + 4y - 2y = 4x + 2y
Encerre com a seguinte pergunta:
Ao abrir a mesa, é possível colocar o dobro de panelas, com as mesmas medidas? E o dobro de pessoas poderão se sentar a mesa?
COMENTÁRIO: Se possível, ilustre as situações acima com fotos.
Professor(a), esse questionamento é importante pois retoma o início da aula e a problematização que tange a área e o perímetro da mesa. A ideia é que ao dobrar a área seja possível colocar o dobro de panelas sobre a mesma, no entanto, quando se abre, não é possível dobrar a quantidade de pessoas para sentar a mesa, uma vez que o perímetro não dobra. No caso da figura 5, se considerarmos que a cada 60 cm é possível “colocar” uma pessoa, conclui-se que, com a configuração original seria possível que se sentassem 4 pessoas, quando a mesa é aberta são seis.
Desta forma, é possível concluir uma importante etapa da aula. É possível levar os alunos a perceberem o que acontece com mesas dobráveis que sejam compostas por mais partes. Para isto, pergunte aos alunos como ficaria a área e o perímetro de uma mesa que se abra em três partes.
Figura 8: Mesa com três partes
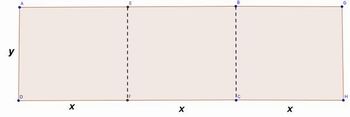
Fonte: Arquivo do autor
Nesse caso tem-se:
- Área: 3.x.y
- Perímetro: 3. (2.x +2.y) – (y + y) – (y + y) = 3.(2.x + 2.y) – 2.y – 2.y = 6.x + 6.y – 4.y = 6.x + 2.y
Professor(a), observe que o raciocínio foi o mesmo. Nesse momento, questione os estudantes para saber se eles conseguem observar algum padrão de regularidade.
Espera-se que eles notem, observando a figura, que o valor de “y” é contado apenas duas vezes.
Como atividade apresente a figura 9, uma mesa que se abre em quatro partes.
Atividade: Utilizando o mesmo raciocínio da aula, escreva a área e o perímetro da mesa abaixo, sabendo que a mesma possui, quando fechada, dimensões “x” e “y”.
Figura 9: Mesa dobrável em quatro partes

Fonte: Disponível em: http://www.casaancora.com.br/media/catalog/product/cache/1/image/9df78eab33525d08d6e5fb8d27136e95/g/1/g1030743.jpg . Acesso em 13 jun. 2014.
Observe que essa mesa possui quatro partes. Caso o estudante tenha percebido o padrão, terá condições de, rapidamente, responder:
- Área: 4.x.y
- Perímetro: 8.x + 2.y
Professor(a), insista no questionamento sobre o padrão. Sintetize com um quadro reunindo os quatro casos:
Quadro 1: Áreas e perímetros
| Número de polígonos | Área | Perímetro |
| 1 | x.y | 2.x + 2.y |
| 2 | 2.x.y | 4.x + 2.y |
| 3 | 3.x.y | 6.x + 2.y |
| 4 | 4.x.y | 8.x + 2.y |
Fonte: Arquivo do autor
E, como atividade final solicite a generalização para “n” desdobramentos.
Atividade: Como podemos escrever a área e o perímetro de um polígono de dimensões “x” e “y” que se desdobra “n” vezes de maneira a sempre manter um lado em comum do polígono anterior com o novo desdobramento?
Figura 10: Mesa com n desdobramentos
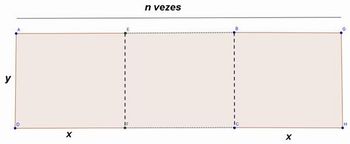
Fonte: Arquivo do autor
Padrão de resposta esperada: Podemos observar que serão n retângulos e, portanto, a área será igual a
n.(x.y) = n.x.y
No caso do perímetro observamos que o “y” é contado apenas duas vezes enquanto o “x” é contado n vezes em cada uma das bases, portanto, o perímetro é dado por
n.x + n.x + y + y = 2.n.x + 2.y
Isso se verifica no quadro 1, observe abaixo o quadro 2, a partir de uma releitura do primeiro.
Quadro 2: Generalizando as áreas e perímetros
| Número de polígonos | Área | Perímetro | |
| 1 | x.y | 2.1.x+2.y | 2.x + 2.y |
| 2 | 2.x.y | 2.2.x+2.y | 4.x + 2.y |
| 3 | 3.x.y | 2.3.x+2.y | 6.x + 2.y |
| 4 | 4.x.y | 2.4.x+2.y | 8.x + 2.y |
| ... | ... | ... | ... |
| n | n.x.y | 2.n.x + 2.y | |
Fonte: Arquivo do autor
Recursos Complementares
Mesas extensíveis
http://www.youtube.com/watch?v=mu15iEPU5kM . Acesso em 03 mai. 2014.
http://www.youtube.com/watch?v=gwjPmP3y6-g . Acesso em 03 mai. 2014.
http://www.youtube.com/watch?v=n_EYGx45dkg . Acesso em 03 mai. 2014.
https://www.youtube.com/watch?v=Ob-wxAE0Y1c . Acesso em 12 jun. 2014.
Avaliação
Feita de maneira continua ao longo da aula, a avaliação deve envolver a participação dos alunos. Há também a possibilidade de que o(a) professor(a) solicite que os(as) alunos(as) façam o registro da última atividade em folha destacada para que possa ser recolhida e, com base nesses registros, concluir o processo de avaliação, verificando se os(as) estudantes compreenderam a generalização.
Sem estrelas 0 classificações
- Cinco estrelas 0/0 - 0%
- Quatro estrelas 0/0 - 0%
- Três estrelas 0/0 - 0%
- Duas estrelas 0/0 - 0%
- Uma estrela 0/0 - 0%
Denuncie opiniões ou materiais indevidos!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


