21/07/2014
Lara Martins Barbosa, Antomar Araújo Ferreira e Angela Cristina dos Santos
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Médio | Matemática | Álgebra/Geometria |
| Ensino Médio | Matemática | Geometria |
| Ensino Médio | Matemática | Álgebra |
O que o aluno poderá aprender com esta aula
A fim de desenvolver as competências da área 2 da Matriz de Referência de Matemática e suas Tecnologias do ENEM, que é utilizar o conhecimento geométrico para realizar a leitura e a representação da realidade e agir sobre ela, bem como resolver situação-problema que envolva conhecimentos geométricos de espaço e forma (H8), são propostos para esta aula o seguinte objetivo:
-
Demonstrar a Lei dos Cossenos via argumentos com áreas de figuras.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
-
Características dos triângulos
-
Área de quadrados e retângulos
-
Definição do cosseno de um ângulo
-
Relações trigonométricas em triângulos retângulos
-
Lei dos Cossenos
-
Noções básicas do Software GeoGebra
Estratégias e recursos da aula
Nesta aula, é apresentada uma atividade investigativa, composta por situações-problemas em que os alunos terão que mobilizar conhecimentos já adquiridos e estratégias, para resolver o problema proposto.
Professor, para o desenvolvimento das atividades propostas nessa aula utiliza-se o Software GeoGebra para auxiliar a construção da figuras/desenhos e compreensão de conceitos geométricos. Além disso, deve-se dispor de um projetor multimídia conectado a um computador com o referido software citado.
Vale lembrar que o software GeoGebra é um programa gratuito e o seu download está disponível em: <http://migre.me/jBiaC>, acesso em 14 jun. 2014. Também é possível utilizar este software online, ou seja, sem realizar sua instalação. Para isso, acesse o link <http://migre.me/jBijx>, acesso em 14 jun. 2014.
Comentário: Essa aula deve ser desenvolvida em um laboratório de informática com um computador por aluno ou em dupla, para possibilitar a interação e acompanhamento das atividades pelos alunos.
O software GeoGebra – apresentação:
Nesta aula, a demonstração da fórmula da Lei dos Cossenos, será estudada com o auxílio do softwareGeoGebra. Segundo Humberto José Bortolossi (s.d.), o GeoGebra, criado por Markus Hohenwarter, é um software gratuito de matemática dinâmica desenvolvido para o ensino e aprendizagem da matemática nos vários níveis de ensino (do básico ao universitário). O GeoGebra reúne recursos de geometria, álgebra, tabelas, gráficos, probabilidade, estatística e cálculos simbólicos em um único ambiente. Assim, o GeoGebra tem a vantagem didática de apresentar, ao mesmo tempo, representações diferentes de um mesmo objeto que interagem entre si.
Figura 1 – Apresentação do Software GeoGebra
Fonte: Arquivo da Autora
Um aspecto importante a ser evidenciado é alertado pelos Parâmetros Curriculares Nacionais do Ensino Médio – PCNEM – (BRASIL, 1999), que afirmam que a inserção de computadores na sociedade em geral “exigirá do ensino de matemática um redirecionamento sob uma perspectiva curricular que favoreça o desenvolvimento de habilidades e procedimentos com os quais o indivíduo possa se reconhecer e se orientar nesse mundo do conhecimento em constante movimento.” (p.252).
Tais orientações e sugestões levam-nos a pensar que a utilização de computadores no ensino de matemática pode desencadear uma nova relação professor-aluno, marcada por uma maior proximidade, interação e colaboração. Esse fato exige uma nova concepção e formação de professor, “que, longe de considerar-se um profissional pronto, ao final de sua formação acadêmica, tem de continuar em formação permanente ao longo de sua vida profissional.” (BRASIL, 1998, p.44).
A LEI DOS COSSENOS...
A Lei dos Cossenos estabelece que: em qualquer triângulo, o quadrado de um dos lados corresponde à soma dos quadrados dos outros dois lados, menos o dobro do produto desses dois lados pelo cosseno do ângulo entre eles, como pode ser visto na figura 2.
Figura 2 – Lei dos Cossenos
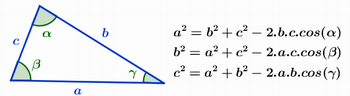
Fonte: Arquivo da Autora
DEMONSTRAÇÃO GEOMÉTRICA A PARTIR DE UM TRIÂNGULO ACUTÂNGULO.
Professor(a), inicialmente, solicite aos alunos que construam um triângulo acutângulo no GeoGebra e marque seus ângulos internos. Aproveite e pergunte quais são as propriedades de um triângulo acutângulo.
Padrão de resposta esperado:
“Triângulo acutângulo é todo triângulo que apresenta os três ângulos internos menores que 90º, ou seja, os três ângulos internos são agudos (figura 3)”.
Figura 3 – Triângulo acutângulo
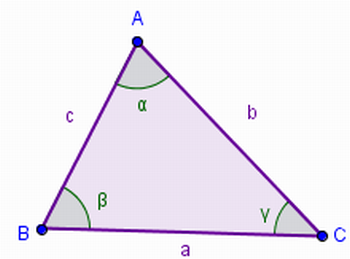
Fonte: Arquivo da Autora
Comentário: Professor(a) a demonstração geométrica também pode ser feita com triângulos obtusângulos, porém optamos pelos triângulos acutângulo para facilitar a construção.
Solicite a construção dos três quadrados sobre os lados do triângulo ABC e das retas que passam pelos ponto A, B e C respectivamente perpendiculares aos seus lados opostos (figura 4).
Figura 4 – Construção dos três quadrados sobre os lados do triângulo ABC
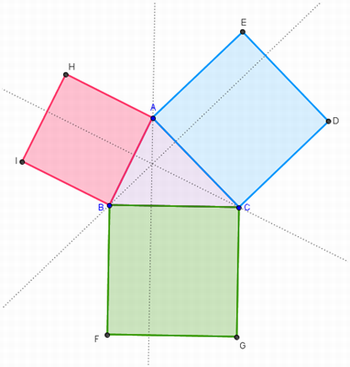
Fonte: Arquivo da Autora
Levante as seguintes questões:
1) O que podemos dizer se considerarmos apenas os segmentos que estão dentro do triângulo ABC?
Padrão de resposta esperado:
“Os segmentos que estão dentro do triângulo ABC são as alturas, pois a altura de um triângulo é um segmento de reta perpendicular a um lado do triângulo ou ao seu prolongamento, traçado pelo vértice oposto”.
Comentário: Talvez seja necessário retomar a definição de altura de um triângulo.
2) O que podemos dizer sobre o ponto de interseção entre as retas traçadas?
Padrão de resposta esperado:
“O ponto de interseção das retas traçadas também é o ponto de interseção das três alturas do triângulo, esse ponto recebe o nome de ortocentro. No triângulo acutângulo, o ortocentro é interno ao triângulo”.
Peça que observem que, quando foram traçadas, as retas dividiram os quadrados em dois retângulos. Solicite que destaquem os retângulos como na figura 5. Para isso, deve-se encontrar os pontos de interseção das retas com os quadrados e então construir os retângulos.
Figura 5 – Destacando os retângulos
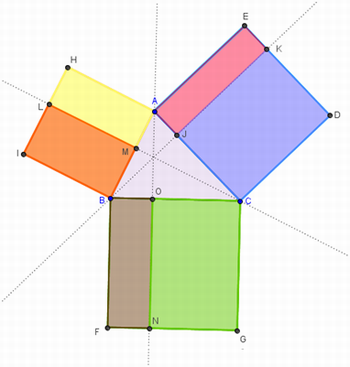
Fonte: Arquivo da Autora
A próxima etapa é investigar como encontrar a medida dos lados desses retângulos.
Levante as seguintes questões:
3) Observando o triângulo AJB, o que podemos dizer sobre ele?
Padrão de resposta esperado:
“O triângulo AJB é retângulo em J”.
4) Sabendo, então, que triângulo AJB é retângulo como, considerando o ângulo com vértice em A e usando as relações trigonométricas no triângulo retângulo e usando o ângulo, podemos encontrar a medida do lado AJ?
Padrão de resposta esperado:
“Das relações trigonométricas de um triângulo retângulos podemos concluir que o segmento AJ = AB.cos(α) . De fato, observe a figura 6, temos que o segmento AB mede c pela construção inicial (figura 3) e sabemos que cosseno de um ângulo é cateto adjacente dividido pela hipotenusa. Logo,
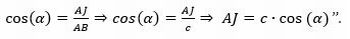
Figura 6 – Relações trigonométricas no triângulo AJB
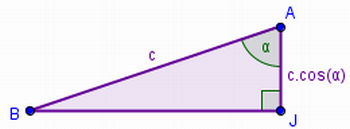
Fonte: Arquivo da Autora
Comentário:Talvez seja necessário retomar a definição do cosseno de um ângulo.
5) Observando o triângulo AMC, o que podemos dizer sobre ele?
Padrão de resposta esperado:
“O triângulo AMC é retângulo em M”.
6) Sabendo, então, que triângulo AMC é retângulo como, considerando o ângulo com vértice em A e usando as relações trigonométricas no triângulo retângulo e usando o ângulo, podemos encontrar a medida do lado AM?
Padrão de resposta esperado:
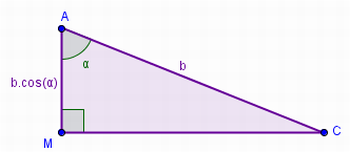
“Das relações trigonométricas de um triângulo retângulo podemos concluir que o segmento AM = AC.cos(α). De fato, observe a figura 7, temos que o segmento AC mede b pela construção inicial (figura 3) e sabemos que cosseno de um ângulo é cateto adjacente dividido pela hipotenusa. Logo,
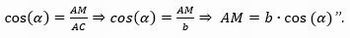
Figura 7 – Relações trigonométricas no triângulo AMC
Fonte: Arquivo da Autora
7) Após analisar esses dois triângulos, o que podemos dizer da área do retângulo rosa (AEKJ) e da área do retângulo amarelo (AHLM)?
Padrão de resposta esperado:
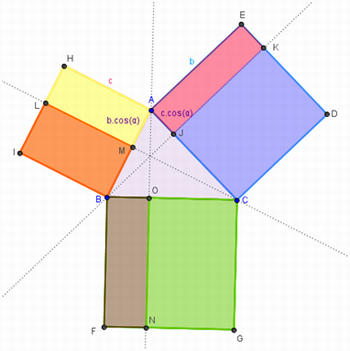
“A área do retângulo AEKJ é dada por b.c.cos(α), e a área do retângulo AHLM é dada por c.b.cos(α). Logo, os dois retângulos analisados são equivalentes, pois possuem a mesma área (figura 8)”.
Comentário: Ressalte, nesse momento, com os alunos que a união desses dois retângulos tem como área o valor dado pela expressão: 2.b.c.cos(α).
Figura 8 – Área dos retângulos AEKJ e AHLM
Fonte: Arquivo da Autora
Agora, devemos mostrar que o retângulo azul (CDKJ) é equivalente ao retângulo verde (CONG).
Levante as seguintes questões:
8) Observando o triângulo BJC, o que podemos dizer sobre ele?
Padrão de resposta esperado:
“O triângulo BJC é retângulo em J”.
9) Sabendo, então, que triângulo BJC é retângulo como, considerando o ângulo com vértice em C e usando as relações trigonométricas no triângulo retângulo e usando o ângulo, podemos encontrar a medida do lado JC?
Padrão de resposta esperado:
“Das relações trigonométricas de um triângulo retângulos podemos concluir que o segmento JC = BC. cos(γ). De fato, observe a figura 9, temos que o segmento BC mede a pela construção inicial (figura 3) e sabemos que cosseno de um ângulo é cateto adjacente dividido pela hipotenusa. Logo,
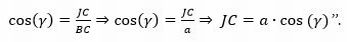
Figura 9 – Relações trigonométricas no triângulo BJC
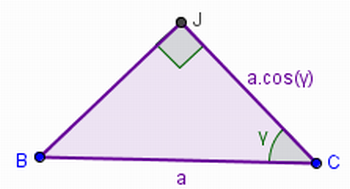
Fonte: Arquivo da Autora
10) Observando o triângulo AOC, o que podemos dizer sobre ele?
Padrão de resposta esperado:
“O triângulo AOC é retângulo em O”.
11) Sabendo, então, que triângulo AOC é retângulo como, considerando o ângulo com vértice em C e usando as relações trigonométricas no triângulo retângulo e usando o ângulo, podemos encontrar a medida do lado OC?
Padrão de resposta esperado:
“Das relações trigonométricas de um triângulo retângulo podemos concluir que o segmento OC = AC.cos(γ). De fato, observe a figura 10, temos que o segmento AC mede b pela construção inicial (figura 3) e sabemos que cosseno de um ângulo é cateto adjacente dividido pela hipotenusa. Logo,
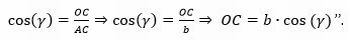
Figura 10 – Relações trigonométricas no triângulo AOC
Fonte: Arquivo da Autora
12) Após analisar esses dois triângulos, o que podemos dizer da área do retângulo azul (CDKJ) e da área do retângulo e verde (CONG)?
Padrão de resposta esperado:
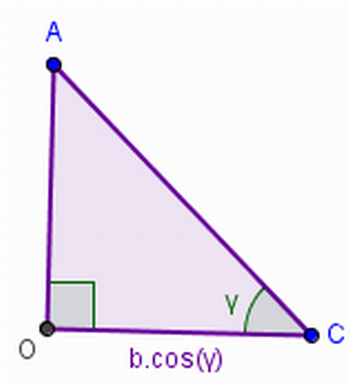
“A área do retângulo CDKJ é dada por b.a.cos(γ), que equivale a área do retângulo CONG dada por c.a.cos(γ). Logo, os dois retângulos analisados são equivalentes, pois possuem a mesma área (figura 11)”.
Figura 11 – Área dos retângulos CDKJ e CONG
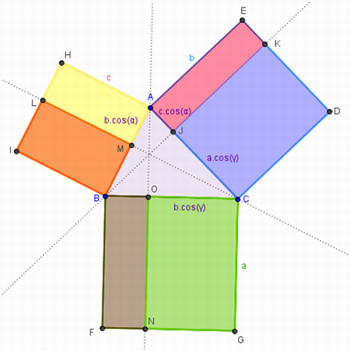
Fonte: Arquivo da Autora
Da mesma maneira devemos mostra que o triângulo laranja (BILM) é equivalente ao retângulo marrom (BONF)
Levante as seguintes questões:
13) Observando o triângulo AOB, o que podemos dizer sobre ele?
Padrão de resposta esperado:
“O triângulo AOB é retângulo em O”.
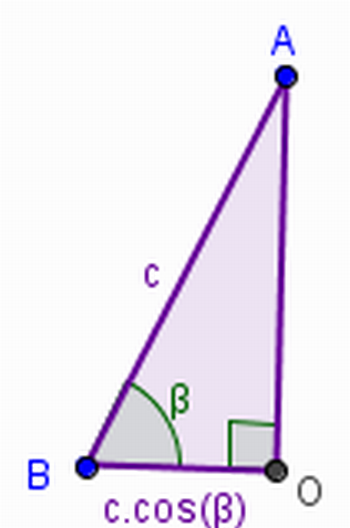
14) Sabendo, então, que triângulo AOB é retângulo como, considerando o ângulo com vértice em B e usando as relações trigonométricas no triângulo retângulo e usando o ângulo, podemos encontrar a medida do lado OB?
Padrão de resposta esperado:
“Das relações trigonométricas de um triângulo retângulo podemos concluir que o segmento OB = AB.cos(β). De fato, observe a figura 12, temos que o segmento AB mede c pela construção inicial (figura 3) e sabemos que cosseno de um ângulo é cateto adjacente dividido pela hipotenusa. Logo,
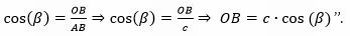
Figura 12 – Relações trigonométricas no triângulo AOB
Fonte: Arquivo da Autora
15) Observando o triângulo BMC, o que podemos dizer sobre ele?
Padrão de resposta esperado:
“O triângulo BMC é retângulo em M”.
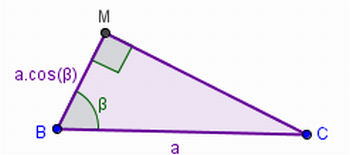
16) Sabendo, então, que triângulo BMC é retângulo como, considerando o ângulo com vértice em B e usando as relações trigonométricas no triângulo retângulo e usando o ângulo, podemos encontrar a medida do lado BM?
Padrão de resposta esperado:
“Das relações trigonométricas de um triângulo retângulo podemos concluir que o segmento BM = BC.cos(β). De fato, observe a figura 13, temos que o segmento BC mede a pela construção inicial (figura 3) e sabemos que cosseno de um ângulo é cateto adjacente dividido pela hipotenusa. Logo,
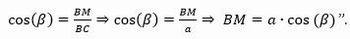
Figura 13 – Relações trigonométricas no triângulo AOC
Fonte: Arquivo da Autora
17) Após analisar esses dois triângulos, o que podemos dizer da área do retângulo laranja (BILM) e da área do retângulo e marrom (BONF)?
Padrão de resposta esperado:
“A área do retângulo BILM é dada por c.a.cos(β), que equivale a área do retângulo BONF dada por c.a.cos(β). Logo, os dois retângulos analisados são equivalentes, pois possuem a mesma área (figura 14)”.
Figura 14 – Área dos retângulos BILM e BONF
Fonte: Arquivo da Autora
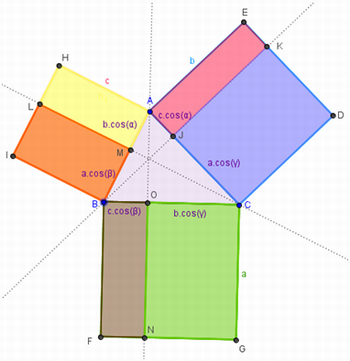
Para finalizar a aula os alunos devem deduzir a fórmula da Lei dos Cossenos geometricamente a partir da figura 15:
Figura 15 – Área dos retângulos
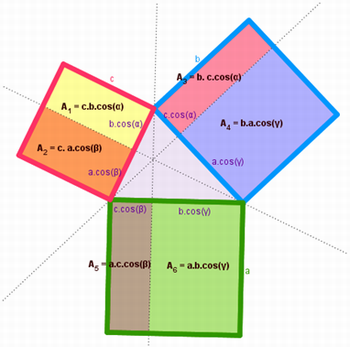
Fonte: Arquivo da Autora
Assim temos que para o ângulo α a área do quadrado verde é igual à soma das áreas dos quadrados azul e rosa menos duas vezes a área do retângulo amarelo.
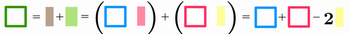
Ou seja,
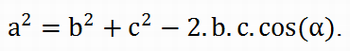
Recursos Complementares
Uma nova linha no ensino de geometria vem recebendo o nome de Geometria Dinâmica. Trata-se da utilização de softwares de construções geométricas que permitem a transformação de figuras mantendo certo número de suas propriedades. Conheça o Software GeoGebra e explore suas inúmeras funções.
É possível encontrar diversas construções realizadas com Software GeoGebra no GeoGebra Tube. Disponível em: <http://migre.me/jKufa>. Acesso em: 14 jun. 2014.
BARBOSA, Lara Martins; BERTONE, Ana Maria Amarillo; MARCO, Fabiana Fiorezi de. GeoGebra e a lei dos cossenos sem palavras: uma nova prova cortando e pegando. In: Libro de Resúmenes del Congreso Latinoamericano de GeoGebra. Argentina, 2013. (p. 72).
Avaliação
Observe o envolvimento dos alunos, individual e coletivamente, na realização dos processos solicitados, sua motivação e empenho na execução das atividades e no desenvolvimento de atitudes na interação, cooperação e organização do trabalho em grupo. Aconselha-se que o (a) professor (a) considere as hipóteses levantadas e os questionamentos dos alunos durante a aula. As construções dos alunos podem ser salvas para serem avaliadas pelo professor, posteriormente, assim, o (a) professor (a) pode analisar as habilidades desenvolvidas, as estratégias e os cálculos efetuados pelos alunos, além de possíveis erros uma possível reelaboração de estratégias de intervenção didática para orientar os alunos a buscarem o caminho certo.
Sem estrelas 0 classificações
- Cinco estrelas 0/0 - 0%
- Quatro estrelas 0/0 - 0%
- Três estrelas 0/0 - 0%
- Duas estrelas 0/0 - 0%
- Uma estrela 0/0 - 0%
Denuncie opiniões ou materiais indevidos!
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


