27/11/2009
Fernando Celso Villar Marinho, Lilian Káram Parente Cury Spiller
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Fundamental Final | Matemática | Operações |
| Ensino Médio | Matemática | Geometria |
| Ensino Fundamental Final | Matemática | Álgebra |
O que o aluno poderá aprender com esta aula
Expressar a área de uma figura pela composição da soma e/ou diferença das áreas das partes da figura.
Concluir que a² – b² = (a + b) (a – b).
Transformar a diferença dos quadrados de dois termos em um produto cujos fatores são: a soma desses dois termos e a diferença dos dois termos.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Áreas de quadriláteros: quadrado e retângulo
Operações com números racionais
Operações com polinômios
Estratégias e recursos da aula
Os produtos notáveis são produtos de expressões algébricas utilizados com frequência e que têm regras definidas que facilitam sua determinação.
Inicie a aula, mostrando aos alunos que o produto da soma pela diferença de dois termos é indicado pela expressão: (a + b)(a – b)
Desenvolva a expressão, com a participação dos alunos, recordando as operações com polinômios:
(a + b)(a – b) = a2 – ab + ba – b2
Ou seja, (a + b)(a – b) = a2 – b2
Escreva como se lê:
a2 – b2 é a diferença de dois quadrados
Por exemplo: (x + 2)(x – 2) = x2 – 22 = x2 – 4
Professor, a visualização geométrica é trabalhosa, mas é importante para que os alunos possam rever conceitos, participar ativamente na construção geométrica e perceber as relações entre a álgebra e a geometria.
Para visualização geométrica por parte dos alunos, lembre-os de que:
a2 corresponde à área de uma quadrado de lado a e que b2 corresponde à área de um quadrado de lado b.
Nota: Caso os alunos não se recordem do cálculo das áreas do quadrado e do retângulo, faça uma breve revisão sobre o assunto.
Para tornar a aula mais dinâmica e interativa, sugerimos que seja utilizado material concreto, conforme descrito adiante. Deixamos claro que essa atividade pode ser feita apenas utilizando o quadro negro, mas acreditamos que a participação dos alunos contribuirá na fixação do conteúdo.
Amplie e imprima as figuras abaixo e reproduza em quantidade suficiente para a sua turma. Peça para os alunos recortarem e colorirem de azul o quadrado de lado 3 e de vermelho o de lado 1.
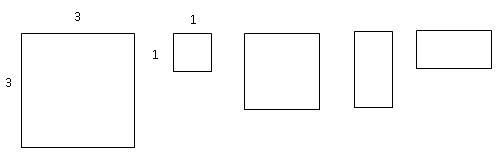
Construa dois quadrados de tamanhos diferentes, como mostra a figura abaixo, em que a medida do lado do quadrado azul é 3 e a do quadrado vermelho é 1.
Note que as medidas de três dos quadriláteros acima, propositalmente, não foram indicadas. Essas medidas deverão ser deduzidas pelos alunos.
Proponha agora sobrepor o quadrado vermelho, colocando-o em um dos cantos do quadrado azul.
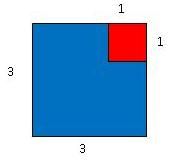
Peça então para os alunos encaixarem os três quadriláteros restantes e registrarem as medidas de seus lados.
Os encaixes resultarão na figura:
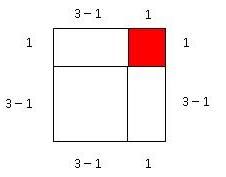
Pergunte aos alunos que parte da figura corresponde a área de 32 – 12 (área do quadrado azul menos a área do vermelho).
Depois que os alunos perceberem que essa área é formada pela soma das áreas de um quadrado de lado (3 – 1) e por dois retângulos de lados 1 e (3 – 1), mostre o rearranjo da figura com a área a ser determinada (explique o deslocamento de um dos retângulos e as medidas indicadas):
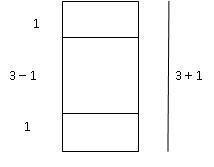
Observando que, com o novo posicionamento de um dos retângulos, a área em questão corresponde à área do retângulo maior de dimensões (3 – 1) e (3 + 1), cujo valor é (3 – 1)(3 + 1).
Conclusão: 32 – 12 = (3 + 1) (3 – 1) e que, portanto, 9 – 1 = 4 x 2 = 8
Se achar conveniente, execute o mesmo pr ocedimento, com as s eguintes medidas para os lados dos quadrados:
1. quadrado a zul: x e quadrado vermelho: 2, concluindo que: x2 – 22 = (x + 2) (x – 2)
2. quadrado azul: 4 e quadrado vermelho: y, concluindo que: 42 – y2 = (4 + y) (4 – y)
3. quadrado azul: a e quadrado vermelho: b, concluindo que: a2 – b2 = (a + b) (a – b)
Nota: É importante relacionar aplicações de produtos notáveis em diferentes contextos matemáticos. Nessa aula, iniciamos com a representação geométrica e obtivemos uma representação algébrica para a diferença de dois quadrados.
Por meio de manipulação algébrica, ou geométrica, foi possível concluir que o produto da soma pela diferença de dois termos é igual a diferença dos quadrados desses termos:
a2 – b2 = (a + b) (a – b).
Uma contextualização interessante para este produto notável é dada para cálculos numéricos do tipo:
1) 51 x 49 = (50 + 1)(50 – 1) = 502 – 12 = 2 500 – 1 = 2 499
2) 37 x 23 = (30 + 7)(30 – 7) = 302 – 72 = 900 – 49 = 851
3) 46 x 34 = (40 + 6)(40 – 6) = 402 – 62 = 1 600 – 36 = 1 564
Recurso disponível em:
http://portaldoprofessor.mec.gov.br/storage/recursos/13092/differenceofsquares.nbp
Nota: Supondo que o quadrado da diferença já tenha sido ensinado, reforce a desigualdade:
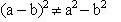
Para obter uma lista de exercícios propostos, acesse o link: http://www.cap.ufrj.br/matematica/PortaldoProfessorMec/atividades/ExercProdutoSomaDif.pdf
Recursos Educacionais
| Nome | Tipo |
|---|---|
| Difference of squares | Animação/simulação |
Recursos Complementares
Avaliação
A avaliação do aluno pode ser feita levando em consideração:
– participação em aula
– resolução de listas de exercícios
– trabalhos em grupo ou individuais, tais como:
• desenhar numa folha de papel quadriculado, dois quadrados de lados que serão informados pelo professor (p. ex., proponha um quadrado de lado x e um quadrado de lado 3) e construir o quadrado perfeito estudado na aula. Nessa proposta deixe-os escolher qual será o maior.
– resolver questões desafio em aula.
Quatro estrelas 5 classificações
- Cinco estrelas 2/5 - 40%
- Quatro estrelas 2/5 - 40%
- Três estrelas 1/5 - 20%
- Duas estrelas 0/5 - 0%
- Uma estrela 0/5 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Adriane Campelo Ramos da Silva, Adriane Campelo Ramos da Silva , Rio de Janeiro - disse:
drikcrs@gmail.com25/03/2015
Cinco estrelasMuito interessante, visto com meu olhar de aluna interessada em matemática.
-
Adriane Campelo Ramos da Silva, Adriane Campelo Ramos da Silva , Rio de Janeiro - disse:
drikcrs@gmail.com25/03/2015
Cinco estrelasMuito interessante. Vendo com meu olhar de aluna interessada em matemática.
-
Justina Motter , Secretaria municipal da educação , Paraná - disse:
jumotter@yahoo.com.br30/04/2012
Quatro estrelasAs demonstrações geométricas apresentadas contribuem significativamente para a apresentação do conteúdo mostrado.
-
Francinete, C.E "INÁCIO PASSARINHO" , Maranhão - disse:
franandrad@hotmail.com14/10/2010
Quatro estrelasParabeniso a professora Rita Maria,pela exposição do assunto de uma maneira mais estratégicas que facilita o entendimento do aluno que não é fácil no desenvolvimento do produto desses termos. Sendo hoje a tecnologia bastante utilizada em sala de aula, seria de grande valia se você desse dicas da utilização dessas ferramentas no assunto exposto.
-
Yuri, Afeganistão - disse:
isablle_nagno@yahho.com04/05/2010
Três estrelasameiiii
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus



