Com esta aula, o aluno poderá desenvolver e/ou aplicar estratégias pessoais de cálculo mental

Para desenvolver as atividades previstas para esta aula o aluno deve dominar as quatro operações fundamentais (adição, subtração, multiplicação e divisão) com números naturais

          Professor, as adivinhações e enigmas são desde a antiguidade assuntos desafiadores e interessantes. Consideramos que seu uso em sala de aula pode trazer potenciais contribuições para o processo de aprendizagem, especialmente no que se refere ao estudo das operações fundamentais com números naturais. Apresentaremos aqui uma sugestão de trabalho nesse sentido, a qual poderá ser adaptada e aprofundada tendo em vista as turmas nas quais for aplicada.
          Num primeiro momento, para o qual imaginamos que seja suficiente uma aula de 50 minutos, sugerimos a você professor que proponha aos alunos algumas situações e/ ou contas e os incentive a resolverem por cálculo mental. É importante lembrar que o cálculo mental aqui comentado, não se restringe a resolução de contas “de cabeça”, muito menos a resolução memorizada das mesmas. O aluno pode ser valer do registro escrito e propor uma estratégia pessoal de resolução. Assim, por exemplo, ao invés de usar o algoritmo tradicional para resolver a operação 3558 + 215, incentive seus alunos a descobrirem estratégias próprias e que sejam mais fáceis de ser computadas mentalmente por eles:

          Em nosso cotidiano, costumamos agrupar os números de maneira diferenciada da tradicional para apresentar as soluções, e não apenas no que se refere à soma, mas também à subtração, à multiplicação e à divisão. Discuta isso com seus alunos, deixe que eles apresentem os diferentes modos como resolvem uma mesma situação, peça para que eles avaliem a viabilidade da aplicação dos métodos sugeridos.
          Algumas adivinhações de domínio público poderão servir como uma boa ferramenta para incentivá-los a aplicarem as estratégias desenvolvidas por eles, nesse primeiro momento. Acreditamos que seja necessário um tempo mínimo de 50 minutos para explorá-las. Na sequencia, alguns exemplos:

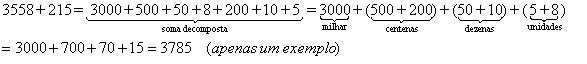
1) Pense em um número. Em seguida some a ele o seu antecessor e o seu sucessor. Dê-me a resposta dessa soma e eu lhe direi o número que você tinha escolhido.
Como descobrir o número pensado: a resposta dividida por 3 dará o número pensado.

2) Vou descobrir a sua idade e o número de pessoas de sua família. Siga os passos abaixo:
a. Multiplique a sua idade por 2.
b. Some 10 ao resultado.
c. Multiplique por 50
d. Some o número de pessoas da sua família.
e. Subtraia 500.
Qual foi o resultado?
Como descobrir a idade e o número de pessoas da família: os dois primeiros dígitos do resultado correspondem a idade e os dois últimos correspondem ao número de pessoas da família.

3) Vou adivinhar o número pensado por você.
         Pense em um número. 
         Multiplique-o por 5.
         Some 6 ao resultado.
         Multiplique por 4.
         Some 9 ao resultado.
         Finalmente multiplique de novo por 5
Qual foi o resultado?
Como descobrir o número pensado: Subtraia 165 do resultado e em seguida divida por 100.

4) Vou descobrir o número do sapato que você calça e a sua idade. Siga os passos abaixo:
         Multiplique o número do seu sapato por 2.
         Some 5 ao resultado.
         Multiplique por 50.
         Subtraia o ano que você nasceu.
Qu al foi o resultado?
Como descobrir a idade o número do sapato e a idade: Subtraia 250 do resultado e em seguida some o ano em que estamos, os dois primeiros dígitos da resposta corresponderão ao número do sapato e os dois últimos a idade.

       Você poderá acrescentar outras adivinhações conhecidas ou ainda pedir aos seus alunos que pesquisem e tragam para discussão.

        Sugestão para trabalhar as adivinhações: apresente aos alunos o enigma (ele pode inclusive ser escrito em um cartaz) e solicite que eles o acompanhe realizando as operações através de cálculo mental, adivinhe as solução es de alguns alunos, exponha para eles como ela foi obtida e organize de modo que os estudantes possam adivinhar os resultados dos demais colegas, aproveitando os cálculos já realizados.

        Se você leciona para alunos de 6ª, 7ª ou 8ª série do Ensino Fundamental (7º, 8º ou 9º anos), pode ainda solicitar aos alunos que justifiquem por meio de equações a maneira através da qual é possível desvendar o enigma. 
        Por exemplo, para a primeira adivinhação proposta uma possível justificativa seria:
Considere sendo x o número pensado. Adicioná-lo ao antecessor e ao sucessor corresponde a fazer a seguinte operação:

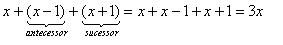
Ou seja, o resultado encontrado equivale ao triplo do número pensando. Desse modo, para descobri-lo basta dividir a resposta por 3.

No momento em que o professor discute e propõe aos alunos a apresentação das soluções, acompanhadas das suas estratégias para realização dos cálculos, surge uma boa oportunidade para avaliação do nível e dificuldade de seus alunos em realizarem o cálculo mental. A partir dessa avaliação, será possível uma reorientação das atividades a fim de possibilitar ao aluno o desenvolvimento de uma maior familiaridade com tais estratégias.