Conceituar, representar graficamente e investigar as propriedades de baricentro e ortocentro.

• Elementos e classificação de triângulos;
• Reta perendicular;
• Distância de reta a ponto;

Professor, para esta aula usaremos o software Geogebra, que além de muito eficiente, é LIVRE. Você encontra o download e um excelente material sobre o uso do software em sua página oficial:
http://www.geogebra.org/cms/
Em sala de aula trabalhe os conceitos e os traçados de alturas e medianas de um triângulo. Para auxiliar na compreensão do conceito de altura, sugiro que você recorte triângulos em papel cartão, faça pequenos furos próximos de cada vértice e pendure um fio de barbante com um peso amarrado na ponta para servir de fio de prumo. Apoie o triângulo em uma mesa sobre um de seus lados. Como o fio de prumo fica sempre perpendicular à mesa, fica fácil para os alunos identificarem a altura do triângulo.

 Divida a turma em grupos, de acordo com a capacidade do laboratório de Informática da sua escola. O ideal é que trabalhem em dupla. Entregue aos grupos um roteiro, como o do exemplo abaixo. Esta é uma atividade de investigação de propriedades. Os alunos deverão anotar respostas no roteiro, que deverá ser entregue a você no final da aula.

Roteiro para investigação de baricentro e incentro.

      Ao iniciar o Geogebra, você encontrará a seguinte tela:

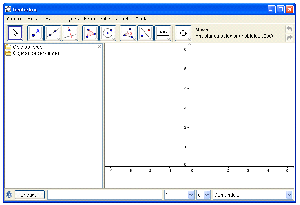
Selecione o menu exibir e desmarque a opção eixo.

1. Selecione a opção polígono . Clique em três lugares diferentes para criar um triângulo ABC. Para fechar o triângulo é necessário clicar sobre o primeiro ponto criado.



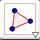
2. Selecione a opção ponto médio e crie os pontos médios dos segmentos AB e BC. Os pontos serão rotulados de D e E, respectivamente.



3. Crie as medianas dos lados ABe BC traçando os segmentos BD e BE com a opção segmento definido por dois pontos .

4. Selecione a opção interseção de dois objetos e crie o ponto de interseção das duas medianas. Este ponto será rotulado automaticamente de F. Crie a terceira mediana. O que você observa? Sabendo que o ponto F é o baricentro do triângulo, defina baricentro.

5. Determine a distância entre os pontos D e F. Faça o mesmo para os pontos F e C. Qual a relação entre essas medidas? Esta relação se mantém para as outras duas medianas? Movimente o triângulo. A relação se mantém? Defina esta relação como uma propriedade do baricentro.

6. Selecione a opção mover e movimente um dos vértices do triângulo. O baricentro sempre fica localizado no interior do triângulo?

7. Construa um novo triângulo. Nomeie de MNO.
8. Com base na definição de altura de um triângulo, construa as três alturas do triângulo MNO usando a ferramenta reta perpendicular. Determine o ortocentro do triângulo.
9. Selecione a opção mover e movimente os vértices do triângulo de modo que ele se torne um triângulo acutângulo. O que você observa em relação a localização do ortocentro?
10. Selecione a opção mover e movimente os vértices do triângulo de modo que ele se torne um triângulo retângulo. O que você observa em relação a localização do ortocentro?
11. Selecione a opção mover e movime nte os vértices do tri ângulo de modo que ele se torne um triângulo obtusângulo. O que vo cê observa em relação a localização do ortoc entro?
12. O que você conclui?

Apostila de atividades com o geogebra:

http://64.233.163.132/search?q=cache:2dwNC_szxEIJ:matematica.110mb.com/conteudo/aula2.DOC+apostila+geogebra&cd=3&hl=pt-BR&ct=clnk

Blog interessante sobre triângulos:

http://valmircirne.blogspot.com/2008/05/pontos-notveis-do-tringulo.html

Site oficial do Geogebra:

http://www.geogebra.org/cms/

Avalie os alunos durante a realização das atividades, observando a participação de cada componente do grupo e a capacidade de trabalhar coletivamente, e através das respostas dadas no roteiro, que deve ser recolhido ao final da aula.