• Realizar medições de superfície com escalas diferentes de medida, abordando
proporcionalidade;
• Formalizar problemas práticos e solucioná-los com o uso da Geometria;
• Identificar simetrias em mosaicos;

• Criar modelos fazendo composições entre polígonos.

Construção de polígonos regulares.
Simetria, reflexão, rotação e translação de figuras planas.

Professor, é interessante que seja feita uma rápida revisão sobre os conceitos de rotação, reflexão e simetria. Você pode encontrar um bom material complementar no link: http://www.professores.uff.br/hjbortol/car/library/rpm-40-mosaicos-do-plano.pdf
Projete algumas imagens que contenham mosaicos geométricos.e, com base nos arranjos geométricos encontrados , faça investigações sobre quais são os polígonos que compõem o mosaico e que tipo de transformações foram usadas.

Por exemplo:

http://www.iessandoval.net/sandoval/aplica/movimientos_plano/geo/mosa1.htm

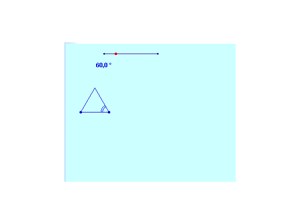
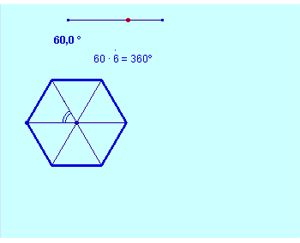
Nesta figura é importante notar que o hexágono pode ser gerado pela rotação do triângulo e que cada conjunto de sete polionos é formado aplicando-se reflexões no primeiro deles.

Otros exemplos:

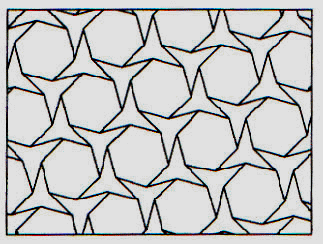
http://www.educ.fc.ul.pt/icm/icm2003/icm16/images/wpe13.gif

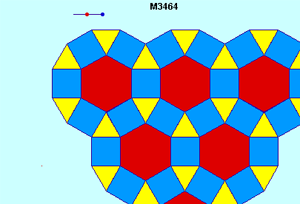
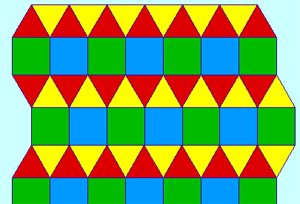
http://www.iessandoval.net/sandoval/aplica/movimientos_plano/geo/mosa1.htm

Questione com os alunos sobre a possibilidade de cobrirmos um plano com qualquer polígono regular. Divida a turma em grupos, e entregue a eles modelos de polígonos regulares feitos em papel e peça que tentem montar mosaicos.

Primeiro, só com quadrados e triângulos e depois, com os pentágonos. Os alunos logo perceberão a impossibilidade de construir um mosaico usando apenas pentágonos. Estabeleça, então, a relação entre os ângulos internos de um triângulo e a pavimentação de um plano.

Como atividade complementar sugiro : pavimentar o piso de uma sala apenas com peças regulares, explicando quantas peças teve que utilizar e o porquê da escolha. A medida da sala de aula pode ser usada como base para a atividade.
No link da figura abaixo você encontra uma apresentação sobre pavimentação, que pode, inclusive ser exibida para os alunos.

Avalie os alunos pela participação na investigação das propriedades das figuras exibidas e na montagem do mosaico. Leve em consideração os seguintes aspectos:
Se os alunos relacionaram os ângulos internos e externos das figuras com as possibilidades de implementação da sua pavimentação;
Se foram aplicadas transformações geométricas.