25/11/2009
Fernando Celso Villar Marinho, Priscila Marques Dias Corrêa
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Fundamental Final | Matemática | Equações |
| Ensino Fundamental Final | Matemática | Álgebra |
| Educação de Jovens e Adultos - 2º ciclo | Matemática | Proporcionalidade e Equivalência |
O que o aluno poderá aprender com esta aula
Resolver equações do 2º grau utilizando o completamento de trinômios quadrados perfeitos.
Deduzir a fórmula de resolução de equações do 2º grau.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Fatoração de trinômio quadrado perfeito
Operação com radicais
Estratégias e recursos da aula
O objetivo dessa aula é manipular equações do segundo grau, obtendo equações equivalentes, de forma a resolvê-las utilizando a fatoração de trinômios quadrados perfeitos. Em seguida, aplica-se esse processo na dedução da fórmula de resolução de equações do 2º grau.
Professor, propomos que a aula seja iniciada com uma breve revisão sobre fatoração de trinômios quadrados perfeitos.
Trinômios quadrados perfeitos:
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2
Proponha a fatoração dos trinômios a seguir, questionando sobre a relação dos termos do trinômio e os da forma fatorada, ou seja, os valores de a e b.
1. x2 + 6x + 9 = (x + 3)2
2. x2 – 10x + 25 = (x – 5)2
Caso haja necessidade, elabore mais alguns exemplos.
Resolvendo as equações dos exemplos dados.
1. x2 + 6x + 9 = 0
(x + 3)2 = 0
x + 3 = 0, então x = –3.
S = {–3}
2. x2 – 10x + 25 = 0
(x – 5)2 = 0
x – 5 = 0, então x = 5.
S = {5}
Questione então sobre a possibilidade de utilizar o mesmo processo para resolver, por exemplo, a equação: x2 – 4x + 3 = 0
Espera-se que os alunos digam que não é possível, pois o trinômio da equação não é quadrado perfeito!
Obs: Caso os alunos já tenham visto equações do tipo: x2 – Sx + P = 0, proponha, então, a resolução:
x2 – 4x + 3 = 0
S = 4
P = 3
Se o produto das raízes é positivo e a soma positiva, então as raízes são positivas e iguais a 1 e 3.
S = {3, 1}
Mostre uma nova forma para resolução da equação, perguntando se é possível obter uma equação equivalente à equação inicial, na qual apareça um trinômio quadrado perfeito. Como dica, peça para os alunos observarem os dois primeiros termos: x2 – 4x e pergunte qual termo que deve ser adicionado a esta expressão para que ela se torne um trinômio quadrado perfeito.
Deixe-os trocar ideias até chegarem ao termo correto: x2 – 4x + 4.
O que fazer então para obter a equação equivalente? Basta utilizarmos o princípio de equivalência, ou seja:
x2 – 4x + 4 + 3 = 0 + 4 (adicionando 4 aos dois membros da equação)
Substituindo x2 – 4x + 4, por (x – 2)2:
(x – 2)2 + 3 = 4 (adicionando –3 aos dois membros da equação), temos: (x – 2)2 = 1
Nota: Lembre-os de que,
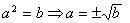
Daí: x – 2 = 1 ou x – 2 = –1
Concluindo então que: x = 3 ou x = 1
S = {3, 1}
Para fixação deste tipo de resolução, sempre com a participação da turma, proponha mais equações.
1) 4x2 + 12x – 7 = 0
Completando o quadrado perfeito em 4x2 + 12x, obtemos o trinômio: 4x2 + 12x + 9.
Adicionando 9 aos dois membros da equação e, em seguida, fatorando o trinômio quadrado perfeito:
4x2 + 12x + 9 – 7 = 0 + 9
(2x + 3)2 – 7 = 9 (adicionando 7 aos dois membros da equação) temos:
(2x + 3)2 = 16
2x + 3 = 4 ou 2x + 3 = –4
Concluindo então que: x = 1/2 ou x = –7/2
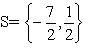
2) – x2 + 14x + 20 = 9
Nota: Para facilitar a manipulação das equações, crie, no aluno, o hábito de multiplicar os dois membros da equação por (–1) sempre que o coeficiente de x2 for negativo.
No caso, (–1) (– x2 + 14x + 20) = (–1) x 9, obtendo:
x2 – 14x – 20 = –9
Completando o trinômio, temos: x2 – 14x + 49
Usando o princípio de equivalência e fatorando, temos:
x2 – 14x + 49 – 20 = –9 + 49
(x – 7)2 = 60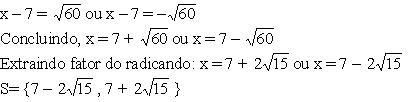
3) 9x2 + 6x = –5
Completando o trinômio, temos: 9x2 + 6x + 1
Usando o princípio de equivalência e fatorando, temos:
9x2 + 6x + 1 = –5 + 1
(3x + 1)2 = –4
Obs: Neste caso, a equação não tem solução real visto que é preciso extrair a raiz quadrada de –4.
Logo, S = { }
4) x2 + x = 6
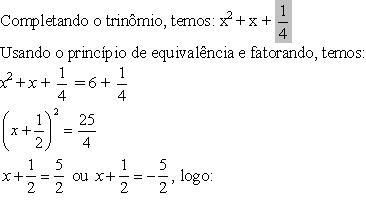
x = 2 ou x = –3
S= {– 3, 2}
Professor, é importante que o próprio aluno deduza a fórmula de resolução de equações do 2º grau, pois, deste modo, não só irá entendê-la, como também poderá fazer a opção de empregá-la ou de resolver uma equação usando o completamento de trinômios.
Para tanto, comece a introduzir letras para representar números. Neste primeiro momento, represente pela letra c o termo independente de x.
Faça-os perceber que o procedimento é o mesmo dos exemplos anteriores.
Exemplo:
Resolver a equação: x2 + x + c = 0

Insira agora a letra b no lugar do coeficiente de x.
Exemplo:
x2 + bx + c = 0

Finalmente, represente o coeficiente de x2 pela letra a, ou seja, considere a equação: ax2 + bx + c = 0
Para garantir que o termo em x2 é um quadrado perfeito, dividiremos ambos os membros da equação por a.

Obs: Informe aos alunos e peça para que registrem em seus cadernos que, para simplificação da representação da equação, costuma-se representar o radicando pela letra grega delta e nomeá-la como sendo o discriminante da equação. Passamos, assim, a representar a fórmula, como abaixo.
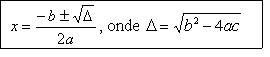
Resolva, com os alunos, algumas equações com o uso da fórmula.
1) –2x2 + 10x – 8 = 0
Dividindo ambos os membros da equação por –2, temos:
x2 – 5x + 4 = 0
Obs: É claro que dividir por (–2) não é necessário, mas facilita, pois trabalha-se com números menores!
Inicie com o cálculo de delta, identificando os valores de a, b e c.
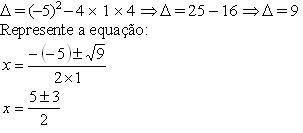
x = 4 ou x = 1
S = {1, 4}
2) x2 – 16x + 64 = 0
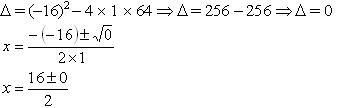
x = 8
S = {8}
3) x2 + 2x = –7
Some 7 aos dois membros da equação, obtendo:
x2 + 2x + 7 = 0
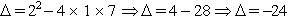
Como o discriminante é negativo, não existe x real. A equação não tem solução.
S = { }
Observando a quantidade de raízes de cada uma das equações resolvidas, peça para os alunos relacionarem essa quant idade com o discriminante das mesmas. Depois que a turma perceber essas relações, solicite que registrem em seus cadernos que:

Lista de exercícios complementares:
http://www.cap.ufrj.br/matematica/PortaldoProfessorMec/atividades/equacoes/ExercEquacoesGrau2.pdf
Recursos Complementares
Link a lista de exercícios.
http://www.cap.ufrj.br/matematica/PortaldoProfessorMec/atividades/equacoes/ExercEquacoesGrau2.pdf
Avaliação
A avaliação do aluno pode ser feita levando em consideração:
– participação em aula
– resolução de listas de exercícios
– trabalhos em grupo ou individuais
– resolução, em sala de aula, de questões desafio
– realização da atividade proposta no link
Quatro estrelas 3 classificações
- Cinco estrelas 2/3 - 66.67%
- Quatro estrelas 1/3 - 33.33%
- Três estrelas 0/3 - 0%
- Duas estrelas 0/3 - 0%
- Uma estrela 0/3 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
luciana, Colégio Professora Janyra de Souza , Bahia - disse:
luciana.custodio2011@hotmail.com17/08/2013
Quatro estrelasmuito boa!
-
Maria Lúcia Panichi Siqueira, Colégio Estadual Luiz Setti-EFMP , Paraná - disse:
luciapanichi@seed.pr.gov.br09/11/2010
Cinco estrelasAchei magnífica sua aula. Muito interessante e de fácil entendimento. Parabéns...
-
Iracena, Colégio Estadual Padre Nestor Maranhão Arzola , Goiás - disse:
iracena_dias@hotmail.com24/03/2010
Cinco estrelasAdorei essa aula.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


