25/11/2009
Fernando Celso Villar Marinho, Priscila Marques Dias Corrêa
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Fundamental Final | Matemática | Álgebra |
| Educação de Jovens e Adultos - 2º ciclo | Matemática | Proporcionalidade e Equivalência |
| Ensino Fundamental Final | Matemática | Equações |
O que o aluno poderá aprender com esta aula
Desenvolver a capacidade de ler, interpretar, escolher estratégias e analisar a solução de uma situação-problema.
Resolver problemas utilizando equações do 2º grau.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Resolução de equações do 1º e do 2º graus
Estratégias e recursos da aula
O enfoque dessa aula é desenvolver no aluno a capacidade de ler, interpretar, escolher estratégias e analisar a solução de uma situação-problema.
Ao abordar cada situação-problema, sempre dê atenção e faça comentários para qualquer solução diferente dada pelos alunos. O importante é que foi feita a leitura, a interpretração, a análise e a escolha de uma estratégia correta para resolução do problema em questão.
Problema 1. Determine três números inteiros positivos e consecutivos tais que o quadrado do menor seja igual a diferença dos outros dois.
Comentários:
Acreditamos que nesse tipo de problema, os alunos têm dificuldade em interpretar corretamente, visto que é muito comum a montagem da equação errada: x2 = (x + 1) – (x + 2).
O quadrado de um número não pode ser negativo, portanto, neste caso, devemos fazer (x + 2) – (x + 1) e não o contrário.
Devemos, então, enfatizar, que a leitura atenta do enunciado é fundamental para uma correta interpretação!
Uma proposta de solução:
Interpretando o problema e usando a linguagem algébrica:
x, representa o menor número
x + 1, representa o consecutivo de x
x + 2, representa o consecutivo de x + 1
Obs: Poderíamos também representá-los por x, x – 1 e x – 2. Nesse caso, x representa o maior dos três números.
Como estratégia de resolução, procedemos a montagem da equação de acordo com o enunciado do problema:
x2 = (x + 2) – (x + 1)
Desenvolvendo, temos:
x2 = x + 2 – x – 1
x2 = 1
Lembrando que:
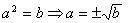
Temos:
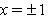
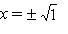
Logo, x = 1 ou x = –1
Analisando a condição do problema, “três números inteiros positivos e consecutivos”, a única solução que satisfaz é x = 1.
Resposta: Os números são 1, 2 e 3.
Problema 2. Pai e filho têm hoje 45 e 15 anos, respectivamente. Há quantos anos a idade do pai era igual ao quadrado da idade do filho?
Comentários:
Em problemas como esse que envolvem tempo decorrido — Há quantos anos... — é importante comentar na turma, que o sinal de menos (–), não significa “retirar” uma quantidade e sim, voltar no tempo! O mesmo vale para situações que se remetem a tempo futuro: “Daqui a quanto tempo...”. O sinal de mais (+) significa avançar no tempo.
Uma proposta de solução:
De acordo com o enunciado, podemos fazer uma representação algébrica das idades do pai e do filho, há x anos.
idade do pai há x anos: 45 – x
idade do filho há x anos: 15 – x
Equalizando as informações: 45 – x = (15 – x)2
Desenvolvendo a equação, obtemos:
45 – x = 225 – 30x + x2Utilizando o princípio de equivalência, temos:
x2 – 29x + 180 = 0
Resolvendo a equação utilizando as relações entre coeficientes e raízes:
S = 29
P = 180
Devemos pensar em dois números positivos (soma e produto positivos).
Os números são: 9 e 20.
Analisando os resultados encontrados, o valor 20 não pode ser usado no problema, pois, nesse caso, o filho teria idade negativa!
Portando, para x = 9 temos para idades: 36 e 6 anos.
Resposta: Há 9 anos.
Problema 3. Um terreno retangular mede 26 m de comprimento e 16 m de largura. Aos fundos do terreno e em uma de suas laterais — como mostra a fig ura a seguir — serão a crescentadas duas faixas de mesma largura. Com essa e xpansão do terreno, a nova área medirá 816 m2. Qual será a largura dessas faixas?

Comentários:
Inúmeras vezes nos deparamos com o questionamento do aluno: “Professor, pra que serve isso?” Essa pergunta, nesse contexto, pode ser respondida com a abordagem de problemas que relacionam a álgebra com a geometria. Os alunos, além de rever conceitos geométricos, podem perceber a relação dos símbolos matemáticos com situações do cotidiano.
Uma proposta de solução:
Interpretando o problema: Com a colocação das faixas, o novo terreno, também retangular, tem dimensões (x + 26) e (x + 16).
Sabendo que a área do retângulo é igual ao produto de suas dimensões e que a nova área é de 816 m2, podemos, então, escrever:
(x + 26)(x + 16) = 816
Desenvolvendo a equação, obtemos:
x2 + 42x +416 = 816
Utilizando o princípio de equivalência, temos:
x2 + 42x + 416 – 816 = 0
x2 + 42x – 400 = 0
Usando o completamento do trinômio e o princípio de equivalência:
x2 + 42x + 441– 400 = 441
Fatorando o trinômio quadrado perfeito e, novamente, utilizando o princípio de equivalência, temos:
(x + 21)2 = 441 + 400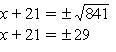
Logo, x = 8 ou x = –40
Analisando os resultados encontrados, o valor –40 não pode ser usado no problema, pois não existem medidas negativas para representar a grandeza “largura”.
Resposta: A faixa terá 8 m de largura.
Problema 4. Quais são as dimensões de um retângulo cujo perímetro e área medem, respectivamente, 50 cm e 150 cm2?
Comentários:
É usual que muitos professores abordem esse tipo de problema quando ministram aulas sobre sistemas de equações do 2º grau. Achamos importante que, ao fazer a interpretação do problema, os alunos percebam que com o uso de apenas uma variável é possível solucioná-lo!
Uma proposta de solução:
Se o perímetro é igual a 50, então o semiperímetro (soma das medidas das dimensões do retângulo) é igual a 25.
Representação algébrica das dimensões do retângulo:
largura: x
comprimento: 25 – x.
Visualizando o retângulo (opcional).
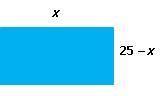
Utilizando o outro dado do problema (área igual a 150), e lembrando que a área de um retângulo é igual ao produto de suas dimensões, podemos afirmar que:
x(25 – x) = 150
Resolvendo, vem que:
25x – x2 = 150 (distributividade)
– x2 + 25x – 150 = 0 (princípio de equivalência)
x2 – 25x + 150 = 0 (princípio de equivalência: multiplicação por –1)
Utilizando a fórmula de resolução de equações de 2º grau: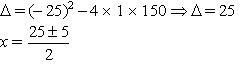
Concluindo que: x = 15 ou x = 10
Analisando as raízes obtidas, podemos concluir que as dimensões do retângulo são 10 e 15 cm.
Resposta: O retângulo tem 10 cm de comprimento e 15 cm de largura.
Problema 5. A figura abaixo é composta por um quadrado com um triângulo em seu interior. A área cinza corresponde a 112 unidades de área. Nessas condições, determine o valor de x.
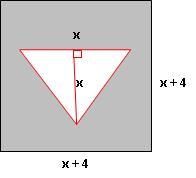
Comentários:
Além da relação entre a álgebra e a geometria enfocada no problema, este requer a visualização e o entendimento de que a á rea cinza pode ser obtida, mais facilmente, por uma diferença de áreas. Situações como essas devem s er abordadas, de modo a contribuir no desenvolvimento do raciocínio lógico do aluno!
Uma proposta de solução:
Analisando a figura, vemos que a área cinza corresponde a área do quadrado menos a área do triângulo.
Lembre-os que:
Área do quadrado (lado l): l2
Área do triângulo (base b, altura h):
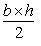
Com os dados das medidas indicadas na figura, o aluno deve representar as áreas algebricamente.
área do quadrado: (x + 4)2
área do triângulo: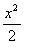
A estratégia utilizada aqui é a da resolução da equação:

2x2 + 16x + 32 – x2 = 224 (princípio de equivalência)
x2 + 16x – 192 = 0 (princípio de equivalência e soma algébrica)
Resolvendo por soma e produto das raízes:
S = –16
P = –192
Devemos pensar em dois números de sinais contrários (produto negativo), sendo o de maior valor absoluto, negativo (soma negativa).
Os números são: 8 e –24
Analisando as raízes da equação, verificamos que a raiz válida é 8.
Resposta: O valor de x é 8.
Problema 6. Um grupo de amigos comprou um camarote no valor de R$1 440,00 para assistir um show. Devido a um contratempo, três dos amigos não puderam ir e o restante resolveu ratear o “prejuízo”, pagando, cada um, R$ 40,00 a mais. Quantas pessoas foram assistir o show?
Comentários:
Esse tipo de problema, que também pode ser resolvido por meio de um sistema de equações do 2º grau, requer uma análise mais detalhada e, provavelmente, os alunos terão dificuldade para interpretá-lo. Por este motivo, sugerimos que sejam dados exemplos numéricos a cada etapa da resolução, conforme exemplificado adiante, para facilitar o entendimento.
Além disto, sabemos que, em geral, os alunos não costumam reler o que está sendo perguntado e a tendência natural é dar como resposta o valor encontrado na resolução da equação. Alerte-os para verificar se a resposta dada corresponde ao que foi perguntado!
Uma proposta de solução:
Interpretando o problema:
Se o valor do camarote é R$ 1 440,00 e havia n amigos, cada um deles pagou o correspondente a 1 440/n.
Clareando as ideias:
Por exemplo, se fossem 10 amigos, cada um pagaria R$ 144,00 (1 440/10).
Com a desistência de três deles, cada um dos n – 3 amigos, pagaram o correspondente a 1 440/n + 40 (R$ 40,00 a mais, conforme enunciado do problema).
Clareando as ideias:
Novamente, se fossem 10 amigos, 7 (10 – 3) pagariam R$ 144,00 + R$ 40,00.
Como o total pago é igual ao número de pessoas multiplicado pelo preço pago por pessoa, concluímos então que:

Logo, n = 12 ou n = –9
No contexto apresentado, a raiz –9 não é válida.
Se eram 12 pessoas inicialmente e três não foram, então nove pessoas assistiram o show.
Resposta: Nove pessoas.
Para obter uma lista de exercícios complementares, clique em
http://www.cap.ufrj.br/matematica/PortaldoProfessorMec/atividades/equacoes/ExercProblemasGrau2.pdf
Recursos Complementares
Link a lista de exercícios.
http://www.cap.ufrj.br/matematica/PortaldoProfessorMec/atividades/equacoes/ExercProblemasGrau2.pdf
Avaliação
A avaliação do aluno pode ser feita levando em consideração:
– participação em aula
– resolução de listas de exercícios
– trabalhos em grupo ou individuais
– resolução, em sala de aula, de questões desafio
Quatro estrelas 13 classificações
- Cinco estrelas 12/13 - 92.31%
- Quatro estrelas 1/13 - 7.69%
- Três estrelas 0/13 - 0%
- Duas estrelas 0/13 - 0%
- Uma estrela 0/13 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Fernanda Pizzigatti M. Jasinevicius, Fernanda Pizzigatti , São Paulo - disse:
ferpizzi@uol.com.br18/06/2015
Quatro estrelasÓtimas sugestões...vou utilizá-las em minha sequência didática e fazer apontamentos em minha dissertação
-
amanda, é nois , Rio Grande do Sul - disse:
zetroveudnove@gmail.com12/05/2015
Cinco estrelasme ajudou muito no trabalho de matematica
-
ANTONIO SILVIO SCHIAVINATO, SESI , São Paulo - disse:
profsilviok@hotmail.com23/03/2015
Cinco estrelasSou professor do Sesi e agradeço por essa ajuda, é MUITO boa mesmo
-
patricia, escola sao jorge , Pernambuco - disse:
papita_232@hotmail.com14/08/2014
Cinco estrelasachei bem legal acho que sempre irei vir para ca pra da uma reforçada nos estudos
-
Ana Paula, Escola do Estado SP , São Paulo - disse:
anap.biologa@gmail.com26/08/2013
Cinco estrelasOs esxercícios são muito bons.
-
Sergio Augusto de Almeida Mendes, Colégio Estadual Baldomero Barbará , Rio de Janeiro - disse:
saugustomendes@bol.com.br12/04/2013
Cinco estrelasSou professor do magistério estadual há doze anos e gostei de conhecer o material, a aula vai nos ajudar bastante no enriquecimento do nosso trabalho, obrigado, pelo presente. Professor Sergio Mendes.
-
Fabiano Nunes, Ormanda Gonçalves , Espírito Santo - disse:
biano1973@yahoo.com.br15/10/2012
Cinco estrelasmuito boa
-
erick, Cefet , Rio de Janeiro - disse:
lazand@oi.com.br25/09/2012
Cinco estrelasMuito boas as resoluções pois me deram uma idéia de como resolver problemas envolvendo equações biquadráticas
-
Carlos Camargo, Particular , Santa Catarina - disse:
cadccamargo@hotmail.com23/08/2012
Cinco estrelasPeço a atenção no problema 3. O resultado desta equação tem raízes X' = 8 e X'' = -50 e não X' = 8 e X'' = -40 como mostra o exemplo.
-
ana paula , escola presidente tancredo neves , Minas Gerais - disse:
paulina.naressi@hotmail.com08/07/2012
Cinco estrelasBom,com a imformação desse site sobre problemas com equação de 2° grau,tive facilidade para montar meu trabalho escolar.
-
matheus, Instituto olavo bilac , Rio de Janeiro - disse:
matheus123@yahoo.com14/05/2012
Cinco estrelasmuito bom
-
Maysa Rossato, Escola Estadual Tenente Aviador Antonio João , Mato Grosso do Sul - disse:
maysa_rossato@yahoo.com.br25/04/2012
Cinco estrelasSou professora de matemática e adorei a sugestão para aula. Abraço!
-
Larissa, .... , Distrito Federal - disse:
lari_lala_rc@hotmail.com22/04/2012
Cinco estrelasAdorei a aula!! Muito bom,me ajudou a interpretar melhor os problemas,antes tinha muita dificuldade agora ficou mais claro.Obrigada
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


