Quando tratamos com objetos sólidos, indeformáveis, o conceito de força aplicada a um ponto é suficiente para descrever o comportamento dinâmico dos objetos. Mesmo assim, é necessário introduzir conceitos como centro de massa e momento da força e dividir o movimento em translação e rotação para uma descrição completa do que realmente acontece.
No caso de fluídos a situação é bem mais complexa. Como os fluídos não têm uma forma definida, a idéia de uma força aplicada em um único ponto não é representativa do que normalmente se observa nas situações reais.
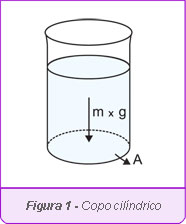
Vejamos um exemplo bastante simples: um copo com água. Como a água tem massa ela sofre ação da força gravitacional e é atraída para baixo com uma força peso (mg). Se o copo for cilíndrico, essa força é aplicada apenas na base do copo, mas não há um ponto de aplicação bem definido. Essa força está distribuída por toda a base do copo. Para descrever como uma força se distribui por uma superfície usamos o conceito de pressão.
A pressão é definida como a razão entre a força F que é aplicada nesta superfície e a área da superfície:
P = F / A (1)
No caso do copo cilíndrico com água, a pressão na base será apenas o peso da água dividido pela área da base. Uma característica importante da pressão é que ela é um escalar e está sempre relacionada com a força normal a superfície em questão.
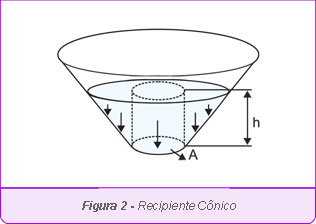
Mas e se o copo fosse substituído por um recipiente cônico? A força peso das massas do recipiente e da água sobre a mesa ainda seria transmitida apenas pela base do recipiente, mas a força peso da água também teria uma componente nas paredes inclinadas do recipiente. Então a força que ela exerceria sobre a base interna do recipiente é menor que a força peso total da massa de água. O peso total estaria distribuído também pelas paredes laterais do recipiente.
E a pressão? Uma característica muito interessante da pressão em um líquido é que ela não depende da forma ou da massa total de líquido, mas apenas da altura do líquido. É como se apenas o líquido que está na coluna sobre a base exercesse uma força sobre o fundo do recipiente. Dizemos que a pressão depende apenas da altura da coluna líquida. Esse comportamento é chamado de Paradoxo Hidrostático. A pressão pode ser calculada por:
p = h·ρ ·g (2)
onde ρ é a densidade do líquido.
O recipiente pode ter qualquer forma e ainda assim esta expressão é válida.
Como os líquidos, os gases também exercem pressão sobre o as paredes dos recipientes que os contêm. Nas aplicações comuns, em que o gás está contido em um recipiente fechado e sua densidade é muito baixa, a pressão é a mesma em todas as paredes do recipiente. Isto quer dizer que podemos ignorar o fato de que o gás tem um peso e que exerce uma pressão no fundo do recipiente um pouco maior do que em cima.
No entanto existe uma situação em que o peso do gás é importante: A atmosfera. A atmosfera é mantida em torno da superfície devido à atração gravitacional. Isto quer dizer que é o peso da atmosfera que a mantém sobre a superfície da Terra. A atmosfera terrestre se estende até uma altura de muitos quilômetros.
Se a densidade do ar fosse constante, poderíamos aplicar a equação (2) para calcular a pressão da atmosfera na superfície. Mas o ar é um gás e sua densidade também depende da pressão; então o cálculo da pressão na superfície é bem mais complicado, mas a pressão pode ser facilmente medida.
Nas aplicações práticas devemos nos lembrar que estamos no fundo de um “oceano ” de ar e que este ar exerce uma pressão sobre todos os objetos.
Para que um líquido seja colocado em movimento - como a água circulando por um cano - é necessário que exista uma diferença de pressão entre as superfícies nas quais o líquido se movimenta. Quanto maior a diferença de pressão, maior será a força resultante sobre a massa de líquido e maior será o fluxo.
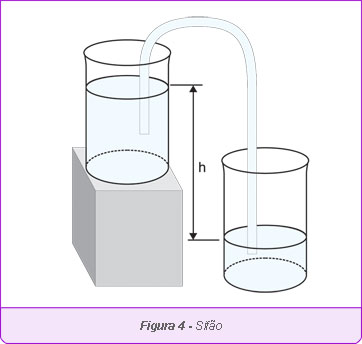
Estes conceitos nos permitem entender o funcionamento do sifão. O sifão é um tubo que une dois reservatórios de líquido e que é usado para transferir o líquido entre eles. Neste experimento, vamos explorar o sifão tentando compreender seu funcionamento em termos das pressões exercidas pelos fluídos envolvidos.
No caso de fluídos a situação é bem mais complexa. Como os fluídos não têm uma forma definida, a idéia de uma força aplicada em um único ponto não é representativa do que normalmente se observa nas situações reais.
Vejamos um exemplo bastante simples: um copo com água. Como a água tem massa ela sofre ação da força gravitacional e é atraída para baixo com uma força peso (mg). Se o copo for cilíndrico, essa força é aplicada apenas na base do copo, mas não há um ponto de aplicação bem definido. Essa força está distribuída por toda a base do copo. Para descrever como uma força se distribui por uma superfície usamos o conceito de pressão.
A pressão é definida como a razão entre a força F que é aplicada nesta superfície e a área da superfície:
P = F / A (1)
No caso do copo cilíndrico com água, a pressão na base será apenas o peso da água dividido pela área da base. Uma característica importante da pressão é que ela é um escalar e está sempre relacionada com a força normal a superfície em questão.
Mas e se o copo fosse substituído por um recipiente cônico? A força peso das massas do recipiente e da água sobre a mesa ainda seria transmitida apenas pela base do recipiente, mas a força peso da água também teria uma componente nas paredes inclinadas do recipiente. Então a força que ela exerceria sobre a base interna do recipiente é menor que a força peso total da massa de água. O peso total estaria distribuído também pelas paredes laterais do recipiente.
E a pressão? Uma característica muito interessante da pressão em um líquido é que ela não depende da forma ou da massa total de líquido, mas apenas da altura do líquido. É como se apenas o líquido que está na coluna sobre a base exercesse uma força sobre o fundo do recipiente. Dizemos que a pressão depende apenas da altura da coluna líquida. Esse comportamento é chamado de Paradoxo Hidrostático. A pressão pode ser calculada por:
p = h·ρ ·g (2)
onde ρ é a densidade do líquido.
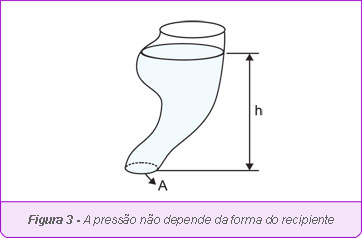
O recipiente pode ter qualquer forma e ainda assim esta expressão é válida.
Como os líquidos, os gases também exercem pressão sobre o as paredes dos recipientes que os contêm. Nas aplicações comuns, em que o gás está contido em um recipiente fechado e sua densidade é muito baixa, a pressão é a mesma em todas as paredes do recipiente. Isto quer dizer que podemos ignorar o fato de que o gás tem um peso e que exerce uma pressão no fundo do recipiente um pouco maior do que em cima.
No entanto existe uma situação em que o peso do gás é importante: A atmosfera. A atmosfera é mantida em torno da superfície devido à atração gravitacional. Isto quer dizer que é o peso da atmosfera que a mantém sobre a superfície da Terra. A atmosfera terrestre se estende até uma altura de muitos quilômetros.
Se a densidade do ar fosse constante, poderíamos aplicar a equação (2) para calcular a pressão da atmosfera na superfície. Mas o ar é um gás e sua densidade também depende da pressão; então o cálculo da pressão na superfície é bem mais complicado, mas a pressão pode ser facilmente medida.
Nas aplicações práticas devemos nos lembrar que estamos no fundo de um “oceano ” de ar e que este ar exerce uma pressão sobre todos os objetos.
Para que um líquido seja colocado em movimento - como a água circulando por um cano - é necessário que exista uma diferença de pressão entre as superfícies nas quais o líquido se movimenta. Quanto maior a diferença de pressão, maior será a força resultante sobre a massa de líquido e maior será o fluxo.
Estes conceitos nos permitem entender o funcionamento do sifão. O sifão é um tubo que une dois reservatórios de líquido e que é usado para transferir o líquido entre eles. Neste experimento, vamos explorar o sifão tentando compreender seu funcionamento em termos das pressões exercidas pelos fluídos envolvidos.
Projeto Acessa Física - Versão 2.0 - Atualizado em 18 de agosto de 2009
Para melhor visualização utilizar Internet Explorer 6.0 ou superior, ou Mozilla Firefox 2.0 ou superior.
 - Esta obra está licenciada sob uma Licença Creative Commons.
- Esta obra está licenciada sob uma Licença Creative Commons.
© 2009 - MEC - Ministério da Educação e Cultura e MCT - Ministério da Ciência e Tecnologia.
Para melhor visualização utilizar Internet Explorer 6.0 ou superior, ou Mozilla Firefox 2.0 ou superior.
 - Esta obra está licenciada sob uma Licença Creative Commons.
- Esta obra está licenciada sob uma Licença Creative Commons.© 2009 - MEC - Ministério da Educação e Cultura e MCT - Ministério da Ciência e Tecnologia.



