Construir segmentos áureos e retângulos áureos.

2 tempos de 50 minutos cada

Resolução gráfica de expressões algébricas.

Professor sugere-se iniciar este conteúdo com a imagem da fachada do Parthenon (século V a.C)

Fig. 1

A fachada do Parthenon construída pelos gregos antigos, que perceberam e aplicaram proporções perfeitas na ciência e na arte, conhecida como divina proporção.
A forma da fachada é um retângulo, mais conhecido como retângulo áureo.
Isto se deve porque sendo um retângulo áureo, seu comprimento (c) está para a sua largura (l) assim como a largura (l) está para a diferença entre o comprimento a largura (c-l):

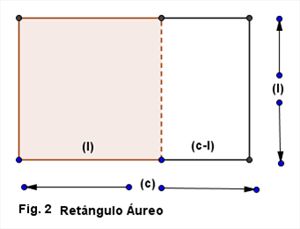
Professor sugere-se o encaminhamento da parte teórica, apresentando a representação gráfica de um segmento, por exemplo:

x/a = y/x ------------> x² = ay ----------> x = raiz ay
(x é a média geométrica entre a e y)
O segmento AP de medida x é chamado segmento áureo de AB.
A razão dessa divisão áurea (x/a) é chamada de razão de ouro.

Atividade Prática 1:
Professor passe para parte do passo a passo da construção do retângulo áureo do qual se conhece a medida de um lado. A construção deverá ter a participação de quatro alunos voluntários, para respectivas etapas:

Construir um retângulo áureo do qual se conhece a medida de um lado.

Pede-se: retângulo áureo DEFG dados: DE = 4 cm
1- Oriente o 1º aluno a desenhar no quadro negro um quadrado DEZT de lado DE, usando o material de desenho do professor, Fig. 1

Fig. 1

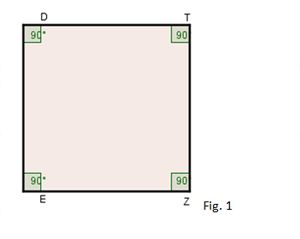
2- Peça ao 2º aluno para determinar um ponto M, ponto médio de EZ; Fig. 2

Fig. 2

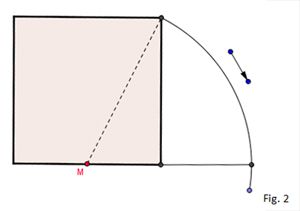
3- O próximo aluno desenhará um arco de centro em M e raio MT, que vai determinar o ponto F em EZ; Fig. 3

Fig. 3

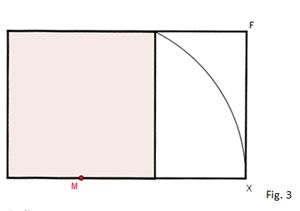
4- O último aluno representará EX que é o lado do retângulo, sendo EZ o segmento áureo de EX. Fig. 4

Fig. 4

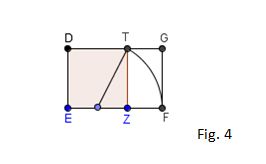
Atividade Prática 2:

Professor a próxima atividade vai requerer a participação de três alunos. A construção agora será do segmento áureo ou divisão de um segmento em média e extrema razão.
Construir o segmento áureo ou divisão de um segmento em média e extrema razão.

Pede-se: o segmento VM, segmento áureo de CA dados: CA
1) Oriente o aluno para construir um  ACP, retângulo em C, cujo cateto AP com a medida de AC/2 .

Fig. 1

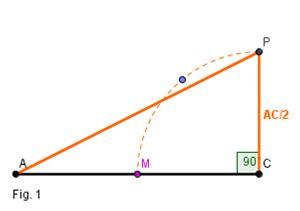
2) O próximo aluno vai subtrair de AC/2 de PA e determinará L na hipotenusa AP.

Fig. 2

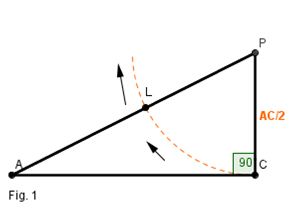
3) O último aluno vai transportar AL para AC, onde determinará o ponto Z. AL é segmento áureo de AC.

Fig. 3

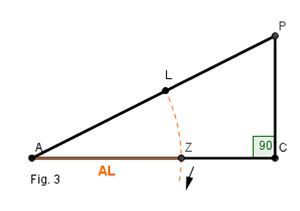
Professor os alunos gostam de participar de atividades no quadro, porque podem utilizar os instrumentos de desenho do professor e prestam mais atenção nos passos a passos das construções.
Proponha para a turma elaborarem duas questões cada um uma da construção do retângulo áureo e outra de segmento áureo para trocarem entre si.

Professor, sugerimos os recursos do software gratuito Geogebra:

http://www.geogebra.org/cms/index.php?option=com_content&task=blogcategory&id=71&Itemid=55

Número de ouro:

http://www.mat.uel.br/geometrica/artigos/ST-15-TC.pdf

Professor, mediante os procedimentos e participação dos alunos, os indicadores para a avaliação poderão ser:

• Os alunos souberam identificar a construção do retângulo áureo?

• Os alunos souberam identificar a construção do segmento áureo?

• As atividades e participação de alguns alunos contribuíram para o envolvimento da turma?

• Os alunos traçaram corretamente ambos as construções gráficas?

• Os alunos elaboraram as duas questões teóricos propostas?