25/02/2009
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Ensino Fundamental Inicial | Matemática | Números e operações |
O que o aluno poderá aprender com esta aula
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Estratégias e recursos da aula
Professor, nesta aula abordaremos o assunto resolução de equações do 2º grau. Apresente situações que utilizem o assunto, tais como:
• Uma sala comercial quadrada tem 81 m2 de área. Quanto mede, em metros, cada lado dessa sala?
• Encontre o número inteiro cujo dobro de seu quadrado adicionado ao seu triplo seja igual a zero.
Professor, geralmente o ensino de resolução de equações do 2º grau é feito de uma forma direta. Nesta aula propomos inicialmente que seja abordado o aspecto histórico, para isto, leve seus alunos ao laboratório de informática e peça a eles que leiam o documento localizado em www.bibvirt.futuro.usp.br/content/download/2373/13519/file/rpm43_04.pdf. O documento em questão trata da abordagem aritmética e geométrica da resolução de equações do 2º grau.
No século IX, o matemático árabe Al-Khowarizmi, escreveu a grande obra matemática chamada “Hisab al-jabr w’al-muqabalah”.

Nesta obra Al-Khowarizmi descreveu métodos para a solução de equações do 2º grau. Acompanhe a seguinte tradução de um fragmento do livro:
“Os números que aparecem nos cálculos pela restauração e pela redução são de três classes: as raízes, os quadrados e os números simples, que não se referem nem às raízes nem aos quadrados [...] Um número que pertence a uma destas três classes pode ser igual a um dos números das outras duas classes, por exemplo: quadrados iguais a raízes; quadrados iguais a números; raízes iguais a números.”, Al-Khowarizmi refere-se aqui a três de equações incompletas. Ele justificou os resultados geometricamente, representado os termos da equação utilizando áreas de retângulos e quadrados, procedimento conhecido por método de completar quadrados. Observe como se resolve geometricamente, utilizando o método de completar quadrados, a equação x2 + 12x = 64, (x2 + bx = c).
Passo 1) Primeiro, desenhe um quadrado de lado "x" para representar o termo x2. Depois, represente o termo 12x por quatro retângulos de lados 3 e "x", como mostra a figura abaixo:
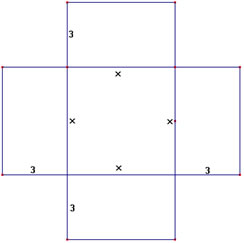
Comentário para os alunos:
• No centro termos um quadrado de lado "x", portanto sua área será x2.
• Em cada retângulo um dos lados mede "x" e o outro a quarta parte do valor do coeficiente "b", (b/4) . Neste caso como o coeficiente "b" é 12, teremos retângulos de medidas "x" e 3, com área 3x.
• A soma das áreas do quadrado e dos quatro retângulos é igual ao coeficiente “c” (termo independente da equação), neste exemplo o valor será 64.
Passo 2) Para completar um quadrado, acrescente quatro quadrados de lado 3.
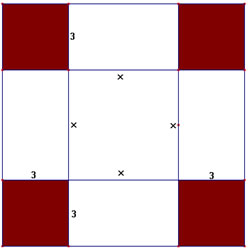
Comentário para os alunos:
• Professor faça alguns questionamentos aos seus alunos como:
* Para completar um quadrado, que figuras devem ser adicionadas à figura anterior?
* Quais são as medidas dessas figuras?
Passo 3) A figura do “Passo 1” tem área de 64. Na figura do “Passo 2” foram acrescentados 4 quadrados de área 9 cada um, totalizando 36, formando um quadrado de área 64 + 36 = 100, portanto um quadrado de lado 10.
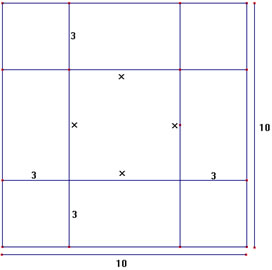
Comentário para os alunos:
• Professor faça alguns questionamentos aos seus alunos como:
* Antes de adicionar essas figuras, a área era de 64, qual será a área depois de se completar o quadrado?
* Como podemos determinar a medida do lado desse quadrado?
* Determinando a medida do lado do quadrado, como podemos determinar a medida x ?
Passo 4) Sendo assim o lado do quadrado formado tem medida 3 + x + 3 = 10 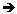 x = 4.
x = 4.
Professor, para aprofundamento do assunto, peça aos seus alunos que resolvam as seguintes equações baixo, utilizando o método de completar quadrados:
a) x2 + 8x = 9
b) x2 + 28x = 60
c) x2 + 20x = 69
Na antiga Babilônia, os escribas conheciam métodos de resolução de problemas equivalentes a certos tipos de equações do tipo x2 – bx = c. Para resolver tais problemas, seguiam regras equivalentes à fórmula:
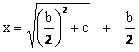
Professor seria interessante que fizesse juntos com os alunos a dedução da fórmula de Bhaskara. Você pode utilizar alguns exemplos em sítios especificados nos recursos complementares desta aula.
Professor, peça a seus alunos leiam um pouco mais sobre o assunto no sítio http://pessoal.sercomtel.com.br/matematica/fundam/eq2g/eq2g.htm#m111a03. Para resolução de equações do 2º grau, utilizado a fórmula de Bhaskara, é muito importante que seus alunos saibam identificar quais são os coeficientes da equação, classificar em completa ou incompleta, calcular o valor do discriminante e em seguida identificar a quantidade de raízes, para isto seria interessante eles montassem uma tabela do tipo:
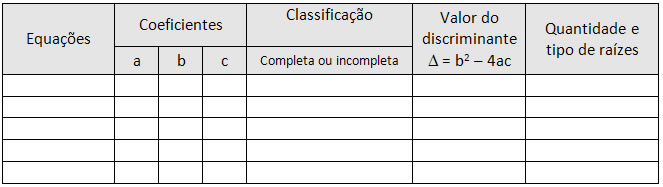
Esta tabela pode ser produzida em um software de planilha eletrônica, como por exemplo BrOffice, http://www.broffice.org/. Professor utilize os diversos tipos de equações incompletas e completas.
Agora vamos calcular as raízes das equações proposta na tabela anterior, para isto peça aos seus alunos que calculem os valores das raízes das equações e em seguida verifiquem o resultado no aplicativo “Raízes”, instalado previamente nos computadores e com download em http://objetoseducacionais2.mec.gov.br/bitstream/mec/4838/1/raizes.zip.
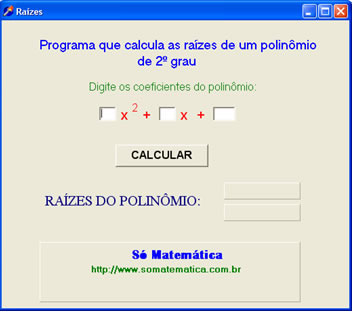
O manuseio do aplicativo é bem simples, basta informar os valores dos coeficientes e em seguida clicar no botão “CALCULAR”. Professor, explore com o aplicativo o estudo do discriminante. Apresente equações onde o valor do discriminante seja:

Caso seja necessário reforçar com atividades on-line em http://www.alunosonline.com.br/barra/index.htm?url=http://www.somatematica.com.br/soexercicios/equacoes2.php.
Professor, para finalizar a aula. Leve seus alunos ao pátio e organize-os em grupos de no máximo 5 pessoas. Coloque para eles a seguinte situação: “Vamos fazer uma horta em um terreno de forma retangular. Nesse terreno, a medida do comprimento é o dobro da medida da largura, mais 4 metros. Quais são as dimensões do terreno, sabendo–se que sua área é 70 m2 ?”. Peça a cada grupo que resolva o problema, identifique as dimensões, calcule a área do retângulo estabelecido e por último, com uma fita métrica, faça no terreno a delimitação do retângulo proposto. Seria interessante ressaltar que com estes cálculos pode-se determinar a quantidade de adubo, fertilizantes e outros produtos a serem aplicados no terreno para a construção da horta.
Recursos Complementares
Avaliação
Quatro estrelas 17 classificações
- Cinco estrelas 7/17 - 41.18%
- Quatro estrelas 9/17 - 52.94%
- Três estrelas 1/17 - 5.88%
- Duas estrelas 0/17 - 0%
- Uma estrela 0/17 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
Eliana Sanches dos Santos, EMEF Arquiteto vilanova Artigas , São Paulo - disse:
lianapromatematica@gmail.com18/11/2016
Cinco estrelasAmei. Foi realmente o que eu estava procurando. Sugestões simples e fáceis para compreensão dos meus alunos . Obrigada. Prof. ELIANA
-
ada.pavanato, toledo barbosa , São Paulo - disse:
ada.pavanato@gmail.com14/05/2013
Cinco estrelasAula bem elaborada. A tabela organiza as informações de forma clara e objetiva. Parabéns!
-
adriano, polo federal do tocantins , Tocantins - disse:
adriano.007gato@hotmail.com22/06/2011
Cinco estrelasgostei muito legal deveria ter uma todo dia
-
Nelson Diniz, Japão - disse:
nerlsir@globo.com19/03/2011
Cinco estrelasQuando estava na escola, fiz a seguinte pergunta para o professor. Em qual situacao da minha vida irei usar a equacao do segundo grau? Ele ficou todo irritado e nao me deu a resposta. Diga la professor aos que nao sabem, onde se usa essa equacao, no dia a dia?
-
Jura, escola , Mato Grosso do Sul - disse:
juraqf@hotmail.com08/09/2010
Quatro estrelasGostei muito, pois aborda a equação do 2º grau de maneira clara para os aluno, mas quem achou que não está bom, porque ainda não postou nenhum trabalho desse tipo.
-
DIEGO DE JESUS FERREIRA, Universidade Federal de Sergipe , Sergipe - disse:
FERREIRAJDIEGO@HOTMAIL.COM26/08/2010
Quatro estrelasmuito clássico, porém legal!!!
-
Robson, E.M. Profª Mª Frca. Tavolaro , São Paulo - disse:
robsongpessoa@ig.com.br23/06/2010
Três estrelasAcho que poderia ter abordado outros exemplos de equações, como x^2 + 2x + 143 = 0 Mas mesmo assim a abordagem foi muito bem elaborada..... Parabéns.
-
luis felipe, choab , Espírito Santo - disse:
chulapa@hotmail.com14/06/2010
Cinco estrelasmuito bom.
-
Alana , colégio da policia militar , Bahia - disse:
lanalovelinda@hotmail.com12/06/2010
Cinco estrelasotima , mas naun entendi uma coizinha que acho que deve ser besteira ... Mas amei muito obirgada !!
-
Célio de Jesus Ferreira, ESC MUL PROF FRANCISCO JOAQUIM DE PAIVA , Goiás - disse:
celiorv2008@gmail.com24/03/2010
Quatro estrelasÓtimo, Parabéns
-
Vera, CEEJA - Ignês de Lamônica Guimarães , Mato Grosso do Sul - disse:
verbakov@hotmail.com24/03/2010
Quatro estrelasGostei muito da sugestão do colega pois além de destacar a importancia da história da matemática, tudo está bem claro para melhor compreensão e aprendizado do aluno. Parabéns.
-
Clodoaldo, Ufvjm , Minas Gerais - disse:
teoemaria@hotmail.com24/03/2010
Cinco estrelasMuito bom um resgate da história da matemática.vale a pena salientar esses aspectos, assim o aluno vê como surgiu aquilo que ele estuda na sala de aula
-
Maria Elizabete Ribeiro Pinto, NAZARE GUERRA EEFM , Ceará - disse:
elizabeteribeiropinto@yahoo.com.br24/03/2010
Quatro estrelasA sugestão de aula do colega professor é muito interessante, pois com essa metodologia os alunos irão adiquirir um melhor aprendizado. Gostei muito dessa metodologia e irei utilizar na minha sala de aula.
-
Sirlaine, Escola Estadual Joaquina Cerqueira Caldas , Mato Grosso - disse:
elai_almeida@hotmail.com24/03/2010
Quatro estrelasGostei muito da sugestão do colega pois além de destacar a importancia da história das equações, e também é claro para melhor compreensão de como surgiu e porque dos termos da equação fazendo com que o aluno tenha um melhor aprendizado. Parabéns.
-
Eliano Paiva, NAZARE GUERRA EEFM , Ceará - disse:
elianopaiva@yahoo.com,br24/03/2010
Quatro estrelasGostei da aula do colega, pois dá ênfase a História da matemática que torna a aula interessante e facilita a compreensão. Não resta dúvida que a utilização das tecnologias melhora o desempenho do aluno e a idéia da planilha é riquíssima é muito louvável.
-
Sirlaine, Escola Estadual Joaquina Cerqueira Caldas , Mato Grosso - disse:
elai_almeida@hotmail.com24/03/2010
Quatro estrelasGostei muito da sugestão do colega pois além de destacar a importancia da história das equações, e também é claro para melhor compreensão de como surgiu e porque dos termos da equação fazendo com que o aluno tenha um melhor aprendizado. Parabéns.
-
ANTONIO ADEGILDO VIANA NUNES, NAZARE GUERRA EEFM , Ceará - disse:
adgildo_viana@hotmail.com24/03/2010
Quatro estrelasGostei muito da sugestão apresentada pelo colega sobre a resolução das equações do 2° grau. Destaco a importância da técnica de completar quadrados para o entendimento do assunto. Aja vista, que é indispensável o uso desse recurso para a compreender a dedução da fórmula de Bhaskara. Elogio, ainda, a sugestão da utilização de planilhas para a construção de gráficos. Acrescento apenas a maior exploração da curva (parábola) dentro da dinâmica da aula.
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus


