17/10/2010
Eziquiel Menta
| Modalidade / Nível de Ensino | Componente Curricular | Tema |
|---|---|---|
| Educação de Jovens e Adultos - 2º ciclo | Matemática | Grandezas e medidas |
| Ensino Médio | Artes | Arte Visual: Contextualização |
| Ensino Médio | Matemática | Geometria |
O que o aluno poderá aprender com esta aula
§ Identificar padrões, pavimentações e simetrias nas obras de Escher.
§ Reconhecer as diferentes simetrias nas obras de Escher.
§ Compor sólidos geométricos planificados com as obras de Escher.
Duração das atividades
Conhecimentos prévios trabalhados pelo professor com o aluno
Conhecimentos prévios de sólidos geométricos e planificação.
Leitura/recepção/apreciação de obras e imagens de obras;
Estratégias e recursos da aula
Atividade 1
Com os alunos divididos em grupos (três ou quatro alunos), encaminhar antecipadamente uma pesquisa (web ou em material impresso) sobre a vida e a obra de Escher.
Para orientar a pesquisa, o professor pode construir uma webquest. A webquest é uma metodologia de pesquisa online, organizada por meio de um roteiro que segue com os seguintes passos: introdução, tarefa, recursos, processo, avaliação, conclusão. O professor dá indicativos de sítios, pré-selecionados, para que a aula seja aproveitada ao máximo, e os alunos não se distraiam diante de tantas informações da internet, e organizem a tarefa e a concluam com sucesso. Para desenvolver sua webquest, o professor pode seguir as orientações do "Tutorial para criar e editar webquest", disponível em: http://rosangelamentapde.pbworks.com/f/tutorial_wq_escolabr1.pdf e, utilizar o sítio http://www.webquestbrasil.org para criar e postar. A ênfase da pesquisa deve abordar sobre a vida e obra de Escher.
Como encaminhamento, o professor pode sugerir que tragam algumas questões como:
1) Onde e quando nasceu?
2) Qual a sua profissão?
3) Qual a técnica utilizada em suas obras?
4) Qual a sua obra de maior destaque?
5) Que relações estabelecem com a Matemática?
6) Curiosidades.
Estas questões deverão ser registradas no caderno, organizando um texto que retrate a vida e obra do autor.
Atividade 2
Após a pesquisa, o professor deve projetar aos alunos algumas obras de Escher, para que os alunos façam observações, identificando qual a figura padrão em cada uma delas.
Sugestão para encaminhamento:
Fonte: http://www.mcescher.com/Gallery/gallery-symmetry.htm
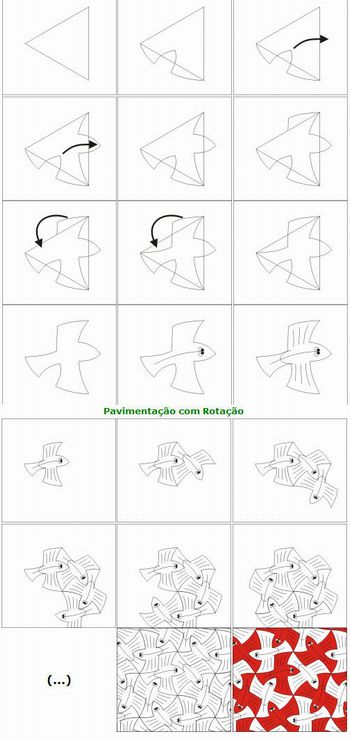
Nas obras de Escher podemos observar pavimentações e simetrias. Um padrão consiste da existência de um “motivo” (Fig. 1), suas cópias, a uma ou mais cores, sobre fundo uniforme (Fig. 2), constituem uma pavimentação. Nas pavimentações a intenção é cobrir o plano completamente, sem área livres e sobreposições. Um padrão pode ser constituído por translações do motivo (Fig. 3), ou rotações e/ou reflexões do motivo (Fig. 4).

Fig. 3 : uma pavimentação
Fonte: http://www.mcescher.com/Gallery/symmetry-bmp/E18.jpg

Fig. 4
Fonte: http://www.mcescher.com/Gallery/symmetry-bmp/E45.jpg
Translação, rotação e reflexão são tipos de simetrias no plano.
No caso das obras observadas, percebemos que em alguns momentos essas imagens são rodadas e/ou invertidas. Para fixação desses conceitos, o professor deve discorrer sobre o tema, apresentando o encaminhamento a seguir:
A simetria ocorre quando é possível encontrar, para qualquer figura, pelo menos uma transformação geométrica diferente da transformação idêntica, que a deixe invariante, isto é, alguns ou todos os pontos da figura podem mudar de posição, mas a figura, como um todo, fica a mesma.
Observe o desenho:
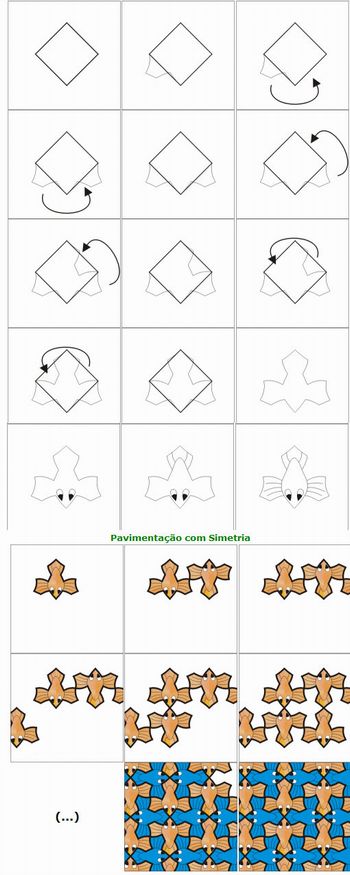
Fonte: http://www.iep.uminho.pt/aac/sm/a2002/M_C_Escher/passo_simetria.htm
O professor pode também apresentar a animação disponível em: http://www.iep.uminho.pt/aac/sm/a2002/M_C_Escher/anim_simetria.htm, acesso em 30 de agosto de 2010.
Na simetria de translação, a figura "desliza" sobre uma reta, mantendo-se inalterada.
Observe o desenho:
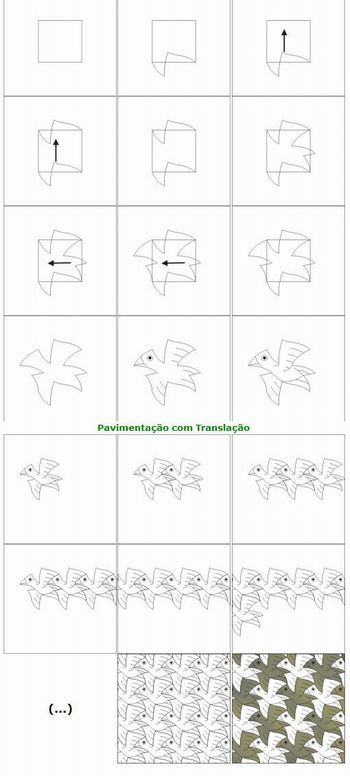
Fonte: http://www.iep.uminho.pt/aac/sm/a2002/M_C_Escher/passo_trans.htm
Se possível, apresentar a animação disponível em: http://www.iep.uminho.pt/aac/sm/a2002/M_C_Escher/anim_trans.htm, acesso em 30 de agosto de 2010.
A simetria de Rotação é a transformação de uma figura que obtemos girando cada um de seus pontos segundo um "arco" de "circunferência" ao redor de um ponto percorrendo um determinado "ângulo".
Observe o desenho:
Fonte: http://www.iep.uminho.pt/aac/sm/a2002/M_C_Escher/passo_rotacao.htm
Apresentar animação disponível em: http://www.iep.uminho.pt/aac/sm/a2002/M_C_Escher/anim_rotacao.htm, acesso em 30 de agosto de 2010.
A simetria de Reflexão ocorre quando uma figura bidimensional possui este tipo de simetria e pode ser refletida em relação a um eixo linear (dito eixo de simetria), de modo a ser possível fazer-se corresponder ponto a ponto com a imagem original.
Observar a obra abaixo que apresenta essa simetria. Imagine um espelho no lugar do traço vermelho. Vale lembrar que a simetria de reflexão não é a única identificada nesta obra. Podemos identificar mais de um tipo de simetria nas obras de Escher.

Fonte: http://www.mcescher.com/Gallery/symmetry-bmp/E45.jpg
Atividade 3
Orientar os grupos que escolham dentre os trabalhos de Escher, um para fazer uma releitura, usando um painel de no mínimo 30x50 de tela, papelão, papel cartão ou tecido; pintando com tintas guache, aquarela, plástica ou acrílica ou ainda lápis ou giz de cera. Identificar na obra o tipo de simetria encontrado, destacando-o. Pode-se solicitar a presença do professor de artes no acompanhamento desta atividade, ajudando os alunos na elaboração da releitura das obras.
Atividade 4
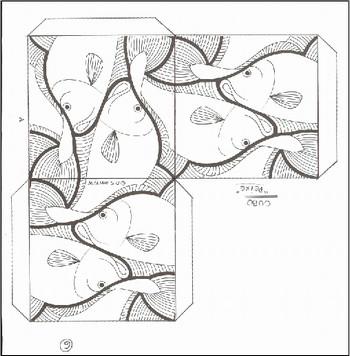
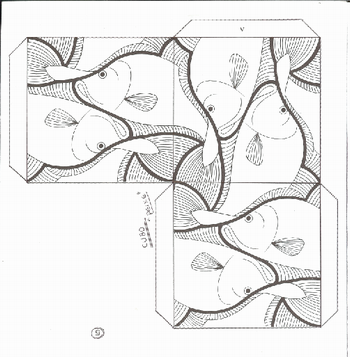
Professor organize para que os grupos possam compor sólidos geométricos (utilizando as obras de Escher nas faces) conforme orientação das figuras abaixo.
Para revisão dos sólidos, apresentar o vídeo Poliedros de Platão, recurso disponível em: http://objetoseducacionais2.mec.gov.br/handle/mec/10627.
Este vídeo apresenta a definição e propriedades dos Poliedros de Platão, caracterizando suas faces, ângulos e arestas, bem como, sua planificação.
No momento das composições converse com os alunos sobre cada possibilidade. Mostre que as simetrias são uma constante nas obras de Escher e por conta disso, é possível decorar as faces de figuras tridimensionais onde as arestas coincidam com os eixos de simetria das imagens. Assim, cada sólido geométrico só pode ser planificado por determinadas obras de Escher.
1 – Cubo - peixes
Fonte: M.C. Escher. Book of Boxes: Taschen,1998. (Ver também http://www.scribd.com/doc/10318375/Taschen-MC-Escher-Book-of-Boxes-100-Years-18981998#fullscreen:on, ou http://www.ebook3000.com/M--C--Escher-Book-of-Boxes_46705.html, acesso em 30 de agosto de 2010.
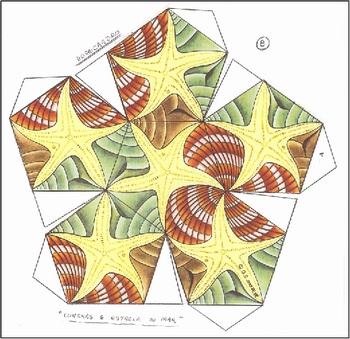
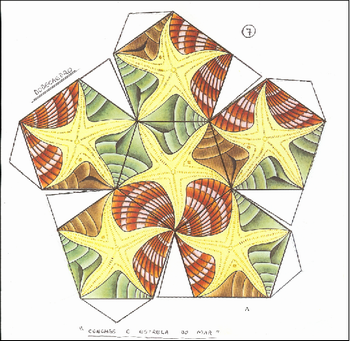
2- Dodecaedro – conchas e estrelas do mar
Fonte: M.C. Escher. Book of Boxes: Taschen,1998. (Ver também http://www.scribd.com/doc/10318375/Taschen-MC-Escher-Book-of-Boxes-100-Years-18981998#fullscreen:on, ou http://www.ebook3000.com/M--C--Escher-Book-of-Boxes_46705.html, acesso em 30 de agosto de 2010.
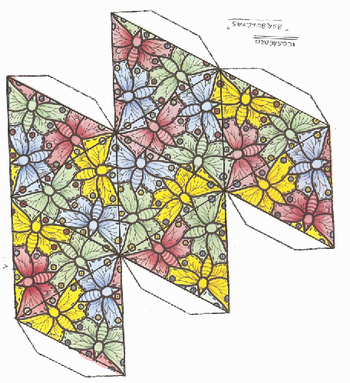
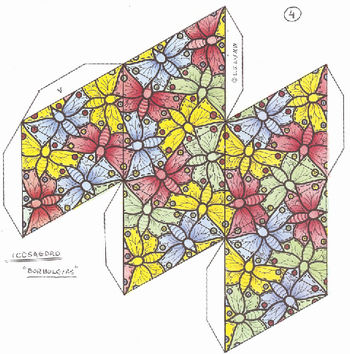
3 - Icosaedro – borboletas
Fonte: M.C. Escher. Book of Boxes: Taschen,1998. (Ver também http://www.scribd.com/doc/10318375/Taschen-MC-Escher-Book-of-Boxes-100-Years-18981998#fullscreen:on, ou http://www.ebook3000.com/M--C--Escher-Book-of-Boxes_46705.html, acesso em 30 de agosto de 2010.
4 - Octaedro – 3 mundos
Fonte: M.C. Escher. Book of Boxes: Taschen,1998. (Ver também http://www.scribd.com/doc/10318375/Taschen-MC-Escher-Book-of-Boxes-100-Years-18981998#fullscreen:on, ou http://www.ebook3000.com/M--C--Escher-Book-of-Boxes_46705.html, acesso em 30 de agosto de 2010.
5 - Tetraedro – Répteis
Fonte: M.C. Escher. Book of Boxes: Taschen,1998. (Ver também http://www.scribd.com/doc/10318375/Taschen-MC-Escher-Book-of-Boxes-100-Years-18981998#fullscreen:on, ou http://www.ebook3000.com/M--C--Escher-Book-of-Boxes_46705.html, acesso em 30 de agosto de 2010.
Ao final desta atividade, para apresentação desses trabalhos e dos outro trabalhos, o professor pode organizar uma exposição, disponibilizando as telas re-criadas na atividade 3, o texto elaborado na atividade 1 e as composições dos sólidos da atividade 4.
Assistir com os alunos o vídeo Decisões Permanentes, disponível em: http://www.diaadia.pr.gov.br/condigital/modules/debaser/singlefile.php?id=14, acesso em 30 de agosto de 2010. Após o vídeo, discutir com os alunos a importância das atividades desenvolvidas nessa aula, da percepção, do olhar diferente e do conjunto de habilidades matemáticas que a envolvem.
M.C. Escher: pavimentações no plano. WebQuest disponível em: http://www.iep.uminho.pt/aac/sm/a2002/M_C_Escher/recursos.htm, acesso em 30 de agosto de 2010.
Aula baseada no vídeo Decisões Permanentes, disponível em: http://www.diaadia.pr.gov.br/condigital/modules/debaser/singlefile.php?id=14, acesso em 30 de agosto de 2010.
Recursos Educacionais
| Nome | Tipo |
|---|---|
| Poliedros de Platão | Vídeo |
Recursos Complementares
Entre a Arte e a Matemática. Disponível em: http://www.educ.fc.ul.pt/docentes/opombo/seminario/escher/escher1.html, acesso em 30 de agosto de 2010.
M.C. Escher. Book of Boxes. Disponível em: http://www.scribd.com/doc/10318375/Taschen-MC-Escher-Book-of-Boxes-100-Years-18981998#fullscreen:on, ou http://www.ebook3000.com/M--C--Escher-Book-of-Boxes_46705.html, acesso em 30 de agosto de 2010.
Metáforas de Escher. Disponível em: http://www.labeee.ufsc.br/~luis/ga/Metaforas-Escher.pdf, acesso em 30 de agosto de 2010.
Mosaico Rendado - A beleza do Kirigami. Disponível em: http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=7993, acesso em 30 de agosto de 2010.
Avaliação
A avaliação deverá ser diagnóstica, processual e continua, ou seja, realizada ao longo de todas as aulas.
Critérios a serem observados:
- Participação na atividade inicial. Realizou a atividade? Colaborou com os colegas? contribuiu na produção?
- Desenvolvimento e realização das atividades? Participou? Raciocínio adequado? O aluno foi argumentativo?
- Participação no desenvolvimento do contexto geral da aula. Participou? Interagiu?
- Apresentação do trabalho. Produção pertinente? Participou?
Quatro estrelas 8 classificações
- Cinco estrelas 6/8 - 75%
- Quatro estrelas 1/8 - 12.5%
- Três estrelas 1/8 - 12.5%
- Duas estrelas 0/8 - 0%
- Uma estrela 0/8 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
-
neidi schuster, EMEF LAURO RODRIGUES , Rio Grande do Sul - disse:
neidischu@zipmail.com.br05/04/2015
Cinco estrelasAchei a proposta das atividades excelente! Pode-se trabalhar as atividades por um longo período com os alunos.
-
Edmundo Silva Guerra, Universidade Federal Rural de Pernambuco , Pernambuco - disse:
edmundoesg@gmail.com06/05/2013
Cinco estrelasAjudou-me bastante no complemento à preparação de um trabalho.
-
EDISON, Colégio Vidal Vanhoni , Paraná - disse:
edisonbranco@ibest.com.br05/03/2013
Quatro estrelasQue delícia de aula. Usarei os desenhos de Escher nas minhas aulas de sala de apoio a aprendizagem.Grato.
-
ruth, E.M.E.F. Giuseppe Garibaldi , Rio Grande do Sul - disse:
claupesc@gmail.com17/08/2012
Cinco estrelasexcelente vou usar nas minhas aulas
-
Chirley Moura, NRE , Paraná - disse:
chirmoura@gmail.com07/04/2012
Cinco estrelasOlá Eguimara! Amei a aula e inclusive irei me apropriar de algumas de suas atividades para a Formação em Ação, muito bom, Parabéns!!!
-
João, África do Sul - disse:
jvjungbluth@hotmail.com24/03/2012
Cinco estrelasMuito interessante, mas precisa de muita paciência
-
Eliana Dalmedico, EE Prof Eduardo Velho Filho , São Paulo - disse:
sotej@ig.com.br13/10/2011
Três estrelasBem elaborado, pesquisas do site , as referencias para buscar mais informaçõese e tambem como fazer as transformações simetricas de rotação.
-
Carmem Artioli, UFT , Tocantins - disse:
carmem.artioli@gmail.com29/09/2011
Cinco estrelasParabéns pela aula, criativa e interdisciplinar
- Sugestão de aula
- Aulas
- Coleções de aulas
- Criar aula
- Criar individual
- Criar em equipe
- Gerenciar equipes
- Minhas aulas
- Orientações
- Criando equipes
- Dicas para a produção de aulas
- Reflexões pedagógicas
- Utilizando a ferramenta
- Artigo: portal educacional
- Estatísticas de uso do Portal
- Estatísticas de aulas
- Estatísticas de recursos
- Estatísticas de visitas
- Recursos utilizados em aulas
- Reflexões pedagógicas
- Informações de cursos
- Cursos
- e-Proinfo
- Materiais de cursos
- Materiais de estudo
- Artigos e publicações
- Assuntos relevantes
- Avaliações
- Ciência do cotidiano
- Destaques internacionais
- Dicas práticas
- Educação profissional e tecnológica
- Entrevistas
- Estratégias pedagógicas
- Inovações tecnológicas
- Materiais de cursos
- Materiais de evento
- Orientações e diretrizes
- Parâmetros e referencias
- Programas em vídeos
- Tutoriais
- TVescola
- Ferramentas do portal
- Fórum
- Portal do Youtube
- Compartilhando apresentação
- Ferramentas pela internet
- Blog
- Compartilhe vídeos
- Comunicação on-line
- Crie e compartilhe apresentações
- Edite e compartilhe fotos
- Escrita colaborativa
- Junte-se a uma comunicade
- Lista de discussão
- Organize e compartilhe favoritos
- Podcast
- Rádio/TVs Universitárias e outros
- Redes Sociais
- Robô Ed
PLATAFORMA FREIRE
- Bibliotecas
- Capacitação Proinfo Integrado
- Cultura
- Dicionários, tradutores e enciclopédias
- Educação inclusiva
- Geoprocessamentos
- Inclusão digital
- Infográficos
- Jogos educativos
- Jornais
- Museus
- Observatórios e planetários
- Organizações governamentais
- Plataformas educacionais
- Portais educacionais e outros
- Portal MEC
- Prêmio professores do Brasil
- Produções de professores
- Projetos de escolas
- Projetos inovadores
- Projetos sociais e educacionais
- Rádio escola
- Recursos digitais
- Revistas
- Sites de busca
- Sites temáticos do portal e TVescola
- Softwares de edição e outros
- Softwares educacionais
- Um computador por aluno

- Ryan Oksenhorn
- Ryan Snow
- Sergio Caldara
- Shane Miler
- Shane Herzog
- Sotirios Papavasilopoulos
- Stephen JB Thomas
- Tarah
- Valera Nazarov
- ZbigniewMa K Flakus





 Poliedros de Platão
Poliedros de Platão